13. Минор матрицы. Ранг м-цы. Базисный минор. Теорема о базисном миноре ( с док-вом)

Минор матрицы ― определитель такой квадратной матрицы порядка (который называется также порядком этого минора), элементы которой стоят в матрице на пересечении строк с номерами и столбцов с номерами

Например, есть матрица:

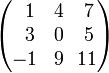
Предположим, надо найти дополнительный минор . Этот минор — определитель матрицы, получающейся путем вычеркивания строки 2 и столбца 3:

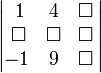
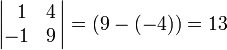
Получаем

Рангом системы строк (столбцов) матрицы с строк и столбцов называется максимальное число линейно независимых строк (столбцов). Несколько строк (столбцов) называются линейно независимыми, если ни одна из них не выражается линейно через другие.

Базисным минором матрицы называется любой её ненулевой минор максимального порядка

.

14. Критерий = 0 определителя.

Определитель =0 если:

а)2 строки одинаковы

б) существует нулевая строка

в)2 пропорциональные строки

г) одна строка есть линейная комбинация остальных

15. Теорема о ранге матрицы (с док-вом).

Ранг матрицы А равен максимальному числу линейно независимых столбцов (или равен рангу системы столбцов матрицы А)

16. Методы вычисл. Ранга м-цы. Утверждение о приведении матрицы к трапец. Форме (с док- вом).

Существует несколько методов нахождения ранга матрицы:

• Метод элементарных преобразований

Ранг матрицы равен числу ненулевых строк в матрице после приведения её к ступенчатой форме при помощи элементарных преобразований над строками матрицы.

• Метод окаймляющих миноров

Пусть в матрице найден ненулевой минор -го порядка . Рассмотрим все миноры -го порядка, включающие в себя (окаймляющие) минор ; если все они равны нулю, то ранг матрицы равен . В противном случае среди окаймляющих миноров найдется ненулевой, и вся процедура повторяется.

17. Определение обратной м-цы, теорема о существовании обратной матрицы (с док-вом).

Обратная матрица — такая матрица A−1, при умножении на которую исходная матрица A даёт в результате единичную матрицу E:

Квадратная матрица обратима тогда и только тогда, когда она невырожденная, то есть её определитель не равен нулю. Для неквадратных матриц и вырожденных матриц обратных матриц не существует.

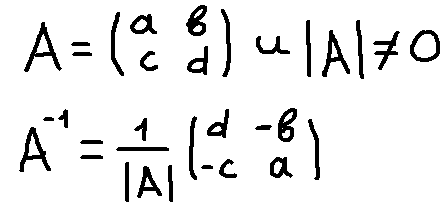
Если определитель матрицы =0, то матрица называется выраженной, обратной не существует.

ТЕОРЕМА о существовании обратной матрицы. Для того, чтобы квадратная матрица А имела обратную матрицу, необходимо и достаточно , чтобы матрица А была невыражденной (detA<>0)

18. Свойства обратных матриц

См. вопрос№17

 , где обозначает определитель.

 для любых двух обратимых матриц и .

 где обозначает транспонированную матрицу.

 для любого коэффициента .

19. Слау. Основные понятия

Система m линейных алгебраических уравнений с n неизвестными (или, линейная система, также употребляется аббревиатура СЛА́У) в линейной алгебре — это система уравнений вида

Система называется однородной, если все её свободные члены равны нулю (b₁ = b₂ = … = b_m = 0), иначе — неоднородной. В общее решение неоднородной системы будет входить общее решение однородной системы и частное решение неоднородной системы

Решение системы  - совокупность чисел c₁, c₂, …, c_n, таких что подстановка каждого c_i вместо x_i в систему обращает все её уравнения в тождества

Решаются методом Гаусса и Крамера