30 Тейлора формула

        формула

        

        

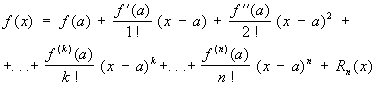
        изображающая функцию f (x), имеющую n-ю производную f ⁽ⁿ⁾(a) в точке х = а, в виде суммы многочлена степени n, расположенного по степеням х—а, и остаточного члена R_n (x), являющегося в окрестности точки а бесконечно малой более высокого порядка, чем (x—a) ⁿ [то есть R_n (x) = an (x)(x—a) ⁿ, где an (x) → 0 при х → а]. Если в интервале между а и х существует (n + 1)-я производная, то R_n (x) можно представить в видах:

        

        ,

        где ξ и ξ₁ — какие-то точки указанного интервала (остаточный член Т. ф. в формах Лагранжа и соответственно Коши). График многочлена, входящего в Т. ф.. имеет в точке а Соприкосновение не ниже n-го порядка с графиком функции f (x). Т. ф. применяют для исследования функций и для приближённых вычислений.

31 Дадим строгое математическое определение понятия неопределенного интеграла.

Выражение вида   называется интегралом от функции f(x), где f(x) - подынтегральная функция, которая задается (известная), dx - дифференциал x, с символом  всегда присутствует dx.

Определение. Неопределенным интегралом  называется функция F(x) + C, содержащая произвольное постоянное C, дифференциал которой равенподынтегральному выражению f(x)dx, т.е.  или  Функцию   называют первообразной функции   . Первообразная функции   определяется с точностью до постоянной величины.

Напомним, что   -дифференциал функции   и определяется следующим образом:

Задача нахождения неопределенного интеграла заключается в нахождении такой функции,производная которой равняется подынтегральному выражению. Данная функция определяется с точностью до постоянной, т.к. производная от постоянной равняется нулю.

Например, известно, что   , тогда получается, что   , здесь   - произвольная постоянная.

Задача нахождение неопределенного интеграла от функций не столь простая и легкая, как кажется на первый взгляд. Во многих случаях должен быть навык работы снеопределенными интегралами, должен быть опыт, который приходит с практикой и с постоянным решением примеров на неопределенные интегралы. Стоит учитывать тот факт, что неопределенные интегралы от некоторых функций (их достаточно много) не берутся в элементарных функциях. 

32-33 Ответов нету 34 Алгоритм метода неопределенных коэффициентов. 

• Во-первых, раскладываем знаменатель на множители. Здесь все методы хороши – от вынесения за скобки, применения формул сокращенного умножения, до подбора корня и последующего деления столбиком (при знаменателе в виде многочлена с рациональными коэффициентами степени выше второй). Об этом подробнее в разделе теории – разложение многочлена на множители. В нашем примере все просто – выносим х за скобки.

• Во-вторых, раскладываемую дробь представляем в виде суммы простейших дробей с неопределенными коэффициентами. Здесь стоит рассмотреть виды выражений, которые могут быть у Вас в знаменателе.

  • Если в знаменателе что-то вроде этого 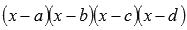 , количество линейных множителей роли не играет, (будь их 2 или 22), то дробь представится в виде суммы простейших дробей первого типа: 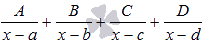a, b, c и d - числа, A, B, C и D - неопределенные коэффициенты.

• Если в знаменателе что-то вроде этого   количество множителей роли не играет и не играют роли степени этих множителей (хоть 221ая степень), то дробь представится в виде суммы простейших дробей первого и второго типов: a, b, c - числа, 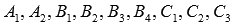  - неопределенные коэффициенты. Возьмите на заметку: какая степень – столько и слагаемых.

• Если в знаменателе что-то вроде этого 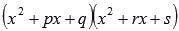  количество квадратичных выражений роли не играет, то дробь представится в виде суммы простейших дробей третьего типа: 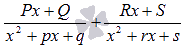p, q, r и s - числа, P, Q, R и S - неопределенные коэффициенты.

• Если в знаменателе что-то вроде этого 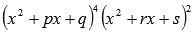  количество множителей роли не играет и не играют роли степени этих множителей, то дробь представится в виде суммы простейших дробей третьего и четвертого типов: p, q, r и s - числа,   - неопределенные коэффициенты. ОБЫЧНО ВСТРЕЧАЕТСЯ КОМБИНАЦИЯ ЭТИХ ВАРИАНТОВ (как правило, довольно простая).

• Если собрать все в кучу 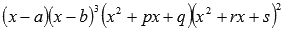 ,то дробь представится в виде суммы простейших дробей всех четырех типов:

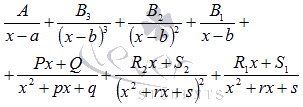
Хватит теории, на практике все равно понятнее. Пришло время вернуться к примеру. Дробь раскладывается в сумму простейших дробей первого и третьего типов с неопределенными коэффициентами A, B и C.

• В-третьих, приводим полученную сумму простейших дробей с неопределенными коэффициентами к общему знаменателю и группируем в числителе слагаемые при одинаковых степенях х. 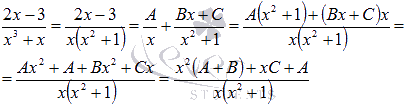То есть, пришли к равенству: При x отличных от нуля это равенство сводится к равенству двух многочленов 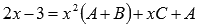А два многочлена являются равными тогда и только тогда, когда коэффициенты при одинаковых степенях совпадают.

• В-четвертых, приравниваем коэффициенты при одинаковых степенях х. При этом получаем систему линейных алгебраических уравнений с неопределенными коэффициентами в качестве неизвестных:

• В-пятых, решаем полученную систему уравнений любым способом (при необходимости смотрите статью решение систем линейных алгебраических уравнений, методы решения, примеры), который нравится Вам, находим неопределенные коэффициенты. О решении систем линейных уравнений подробнее в разделе – решение систем линейных алгебраических уравнений.

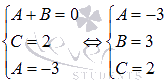
• В-шестых, записываем ответ.

P.S. Пожалуйста, не ленитесь, проверяйте ответ, приводя к общему знаменателю полученное разложение. 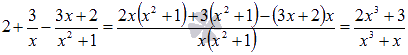Метод неопределенных коэффициентов является универсальным способом при разложении дроби на простейшие. Очень удобно использовать метод частных значений, если знаменатель представляет собой произведение линейных множителей, то есть имеет вид схожий с  Рассмотрим на примере, чтобы показать плюсы этого метода.

Вопрос №35. Функция y = f(x) называется интегрируемой на отрезке [a; b], если существует конечный предел ее интегральных сумм при  , это значение предела называют определенным интегралом и обозначают 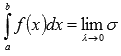  . Где σ - интегральная сумма. Числа a и b называются нижним и верхним пределом интегрирования соответственно, f(x) называется подынтегральной функцией, x – переменной интегрирования. Значение определенного интеграла не зависит от переменной интегрирования, то есть,  .

Свойства определенного интеграла:

1. Для функции y = f(x), определенной при x = a, справедливо равенство   .

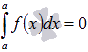2. Для интегрируемой на отрезке [a; b] функции выполняется   .

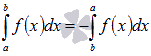3.  для интегрируемых на отрезке [a; b] функций y = f(x) и y = g(x).

4. Постоянный множитель можно выносить за знак определенного интеграла. То есть, для интегрируемой на отрезке [a; b]функции y = f(x) и произвольного числа k справедливо равенство   .

5. Пусть функция y = f(x) интегрируема на интервале X, причем 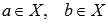  и  , тогда 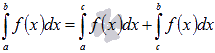 . Это свойство справедливо как для 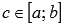 , так и для   или  .

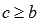6. Если функция интегрируема на отрезке [a; b], то она интегрируема и на любом внутреннем отрезке 

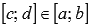
Формула Ньютона-Лейбница:

 

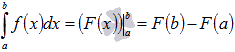
Замена переменной в определенном интеграле:

ТЕОРЕМА. Пусть функция φ(t) имеет непрерывную производную на отрезке [α,β], а=φ(α), в=φ(β) и функция f(х) непрерывна в каждой точке х вида х=φ(t), где t [α,β].

Тогда справедливо следующее равенство:

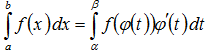
Эта формула носит название формулы замены переменной в определенном интеграле.

Подобно тому, как это было в случае неопределенного интеграла, использование замены переменной позволяет упростить интеграл, приблизив его к табличному (табличным).

Пример. Вычислить 

Положим t=2-х². Тогда dt=d(2-х²)=(2-х²)'dx=-2xdx и xdx=- dt. Если х=0, то t=2-0²=2, и если х=1, то t=2-1²=1. Следовательно:

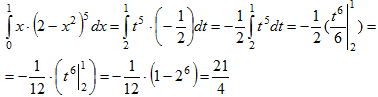
Вопрос №36. Криволинейные интегралы имеют многочисленные приложения в математике, физике и прикладных расчетах. В частности, с их помощью вычисляются

• Длина кривой;

• Площадь области, ограниченной замкнутой кривой;

• Объем тела, образованного вращением замкнутой кривой относительно некоторой оси.

Длина кривой

Пусть C является гладкой, кусочно-непрерывной кривой, которая описывается вектором  . Длина данной кривой выражается следующим криволинейным интегралом

где   − производная, а   − компоненты векторной функции  .  Если кривая C задана в плоскости, то ее длина выражается формулой

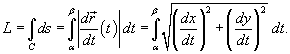
Если кривая C представляет собой график заданной явно, непрерывной и дифференцируемой функции   в плоскости Oxy, то длина такой кривой вычисляется по формуле

Наконец, если кривая C задана в полярных координатах уравнением  , и функция  является непрерывной и дифференцируемой в интервале  , то длина кривой определяется выражением

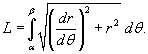
Площадь области, ограниченной замкнутой кривой

Пусть C является гладкой, кусочно-непрерывной и замкнутой кривой, заданной в плоскости Oxy (рисунок 1). Тогда площадь области R, ограниченной данной кривой, определяется формулами

Здесь предполагается, что обход кривой C производится против часовой стрелки.  Если замкнутая кривая C задана в параметрическом виде  , то площадь соответствуюшей области равна

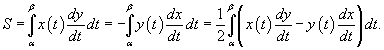
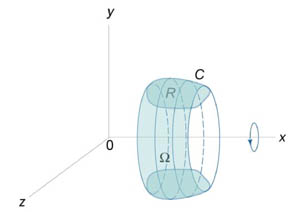
Рис.1		Рис.2

Объем тела.

Предположим, что область R расположена в верхней полуплоскости y ≥ 0 и ограничена гладкой, кусочно-непрерывной и замкнутой кривой C, обход которой осуществляется против часовой стрелки. В результате вращения области R вокруг оси Ox образуется тело Ω (рисунок 2). Объем данного тела определяется формулами

Вопрос №37.

Предположим, что функция   задана на бесконечном промежутке вида   и интегрируема на любом конечном отрезке   , где   . Таким образом, мы можем рассмотреть функцию

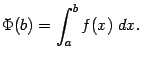
Если эта функция имеет предел   то число   называется значением несобственного интеграла первого рода

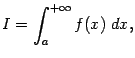
а сам интеграл   называется сходящимся (иными словами, интеграл   сходится).

Если же предела   не существует (например, если   при   ), то интеграл   называется расходящимся (то есть расходится) и не имеет никакого числового значения.     

Геометрически, в случае   , величина несобственного интеграла   означает, по определению, площадь бесконечно длинной области   , лежащей в координатной плоскости между лучом   на оси   , графиком   и вертикальным отрезком   (см. рис.).

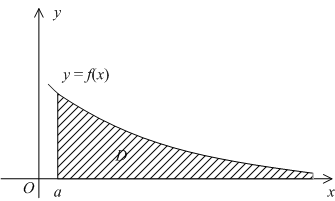
Рис.4.1.

Сходящиеся интегралы соответствуют таким областям   , площадь которых конечна (хотя сама область   неограничена), а расходящиеся (в случае   ) -- неограниченным областям с бесконечной площадью. В случае, когда   при   , часто пишут формально:

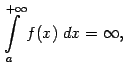
однако нужно ясно понимать, что эта запись означает расходимость интеграла и отсутствие у него числового значения.

Само определение значения интеграла через предел интегралов по конечным, но увеличивающимся отрезкам означает исчерпание площади   путем учёта все большей её части 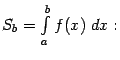  правый вертикальный отрезок, проведённый при   , отодвигается всё дальше и дальше в бесконечность; в пределе будет учтена вся площадь под графиком   (см. рис.).

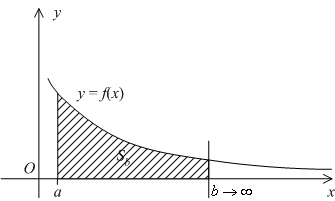
Рис.4.2.

Вопрос №38.

Пусть на полуинтервале   задана функция   , интегрируемая на любом отрезке   , где   , однако не интегрируемая на отрезке   . В точке   эта функция может быть вовсе не определена и стремиться к   при   , любо вовсе не иметь никакого предела при этой базе. Рассмотрим функцию

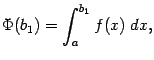
она определена при   . Эта функция   может иметь предел при   (левосторонний предел). Этот предел мы будем называть значением интеграла от   по всему полуинтервалу   и обозначать в точности как обычный интеграл:

Итак, дадим такое определение:

       

 Определение 4.6   Пусть функция   удовлетворяет указанным выше условиям на   . Несобственным интегралом второго рода назовём тогда интеграл

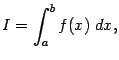
значение   которого равняется левостороннему пределу

Если этот предел существует, то несобственный интеграл называется сходящимся, а если предела не существует, то расходящимся. Расходящемуся интегралу не приписывается никакого числового значения; в этом случае будем условно писать

    

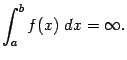
Геометрически вычисление несобственного интеграла второго рода представляет собою (при   ) исчерпание плошади неограниченной фигуры под графиком функции   над   с помощью вычисления плошадей ограниченных фигур, получающихся над отрезком   , а затем приближением правого конца   к точке   (см. рис.).

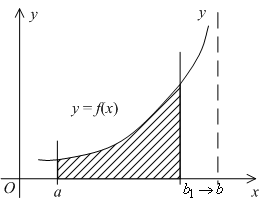
Рис.4.7.

Итак, площадь неограниченной фигуры, изображённой на рисунке, по определению равна значению несобственного интеграла   .

Вопрос №39.

1 Сумма вида   называется интегральной суммой для функции f(x, y) в области D.

Замечание. С геометрической точки зрения (при  ) интегральная сумма представляет собой сумму объемов цилиндров с основаниями ΔS_i и высотами f(P_i).

1. Если существует один и тот же предел интегральных сумм при   и  , не зависящий от способа разбиения области D и выбора точек P_i , то он называется двойным интегралом от функции f(x, y) по области D и обозначается                        .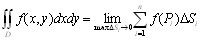                       

Область D при этом называется областью интегрирования.

2. Теорема существования двойного интеграла. Если подынтегральная функция непрерывна на области D, то она интегрируема по этой области.

Вопрос №40.

1.    Геометрический смысл двойного интеграла.  Если z = f(x; y) - положительна на D, то интеграл равен объему цилиндрического тела:

2.          —  площадь области D.

Здесь    которое ограничено: снизу - областью D на плоскости Оxy, сверху - поверхностью z = f(x; y), но z = 1  это цилиндрическое тело есть прямой цилиндр высоты Н = 1 с основанием D 

что и требовалось доказать.

6.    Оценка двойного интеграла снизу и сверху: если  , то    где S - площадь области D.

Теорема 2.2 (О среднем значении для двойного интеграла).

Если f(x; y) — непрерывна на замкнутой области D, то существует M_* D — некая "средняя" точка области: