18. Интегрируемость непрерывной функции на отрезке.

Теорема. Функция, определённая и непрерывная на некотором отрезке, интегрируема на этом отрезке.

Доказательство. Пусть функция f непрерывна на отрезке [a,b]. Их непрерывности функции на отрезке, во-первых, следует её ограниченность, а во-вторых, её равномерная непрерывность на этом отрезке, то есть (1), где ω(δ,f) – модуль непрерывности функции f. Согласно свойству интегральных сумм Дарбу, для любого разбиения отрезка [a,b] , где ωi(f) – колебания функции f на отрезке [xi-1,xi], i = 1,2…k. Замечая что , имеем .

Отсюда в силу (1) следует, что , поэтому функция f интегрируема на отрезке [a,b]. Теорема доказана.

19. Интеграл по направленному отрезку. Цепное правило

Если функция f интегрируема на отрезке [a,b] и a<c<b, то

Если - разбиения соответственно отрезков [a,c] и [c,b], то объединение этих разбиений является разбиением отрезка [a,b], причем

Пусть - какие-либо интегральные суммы Римана функции f, соответствующие разбиениям , тогда - интегральная сумма Римана функции f на отрезке [a,b]

Поэтому, перейдя к пределу в равенстве , при условии , получим

Замечание:

Формула остается в силе и при , если только ф-ция f интегрируема на отрезке [a,c].

В самом деле, если , то, следовательно

20. Свойства определенного интеграла. Неравенства, теорема о среднем для определенного интеграла.

Основные свойства определенного интеграла: 1.

2. Линейность интеграла: Если функция f и g интегрируемы на отрезке [a,b], то при любых функция также интегрируема на отрезке [a.b] и

3. Если функция f интегрируема на отрезку [a,b], то она интегрируема и на любом отрезке .

4. Аддитивность интеграла. Если функция f интегрируема на отрезке [a,b] и a<c<b, то

5. Интегрируемость произведения интегрируемых функций. Если функции f и g интегрируемы на некотором отрезке, то их произведение также интегрируемо на этом отрезке.

6. Интегрирование частного интегрируемых функций. Если функции f и g интегрируемы на некотором отрезке и абсолютная величина функции g ограничена на нем снизу положительной постоянной, то частное также интегрируемо на этом отрезке.

7. Интегрирование неравенств Если функции f и g интегрируемы на отрезке [a,b] и

То

В частности, если , то

8.Если функция f интегрируема и неотрицательна на отрезке [a,b], существует точка , в которой функция F непрерывна и , то

9. Если функция f интегрируема на отрезке [a,b], то её абсолютная величина |f| интегрируема на нем и

10. Непрерывность интеграла. Если функция f интегрируема на отрезке [a,b], то функции

Непрерывны на этом отрезке

Интегральная теорема о среднем.

Теорема:

Пусть на отрезке [a,b]:

1)Функции f и g интегрируемы

2)

3)функция g не меняет знака

Тогда существует такое число , что

Следствие: Если в дополнение к условиям теоремы функция F непрерывна на отрезке [a,b], то на интервале (a,b) существует такая точка , что

21. Интеграл с переменным верхним пределом. Непрерывность интеграла с переменным верхним пределом.

Пусть ф-ция f(x) интегрируема на [a,b]. Тогда, функция f(x) интегрируема на сегменте [a,x]. Поэтому на интервале (a,b) определена ф-ция которую называют интегралом с переменным верхним пределом.

-Если функция f интегрируема на отрезке [a,b], то функции

Непрерывны на этом отрезке.

Функция f, интегрируемая на отрезке [a,b], ограничена на нем, поэтому существует постоянная >-, что выполняется неравенство

Представим интеграл в виде суммы.

Приращение функции F(x) можно записать в виде

Поэтому

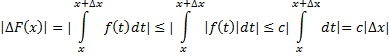
Отсюда следует, что , т.е. непрерывность функции F(x).

Свойство непрерывности функции функции F называется непрерывностью интеграла по верхнему пределу интегрирования.

22. Интеграл с переменным верхним пределом для непрерывной функции.

Если функция f(x) интегрируема в промежутке [a,b], то она интегрируема и в промежутке [a,x], где x есть любое значение из [a,b]. Заменив предел b определенного интеграла переменной x, получим выражение

которое, очевидно, является функцией от x. Эта функция обладает следующими свойствами:

1)Если функция f(x) интегрируема в [a,b], то будет непрерывной функцией от x в том же промежутке

Док-во: Придав x произвольное приращение получим новое значение функции

Так что

Применим к этому интегралу теорему о среднем значении

Здесь содержится между точными границами m’ и M’ функции f(x) в промежутке [x,x+h] , а, следовательно, и между границами основного промежутка [a,b]

Если устремить H к нулю, то, очевидно

Что доказывает непрерывность функции .

2)Если функцию f(t) предположить непрерывной в точке t=x, то в этой точке функция имеет производную, равную f(x):

Док-во: Из (1) имеем

при t=x,

Имеют место неравенства

Следует, что

Для непрерывной в промежутке [a,b] функции f(x) всегда существует первообразная.

23.Формула ньютона-Лейбница для произвольной непрерывной функции.

Пусть ф-ция f(x) интегрируема в промежутке [a,b], а непрерывная в [a,b] ф-ция F(x) имеет f(x) своей производной: F’(x)=f(x)

Разобьем промежуток [a,b] произвольным образом на части точками . Будем иметь

Применим к каждой из разностей формулу конечных приращений:

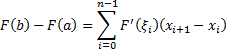
Где есть некоторое определенное значение x между . Так как для этого значения , можем написать .

Отсюда вытекает, что

Заменив в формуле b на x, а f(x) на F’(x) можно написать её в виде