9.Криволинейная трапеция. Геометрический смысл интеграла от положительной функции.

Определим площадь криволинейной трапеции ABCD. Эта фигура ограничена сверху кривой DC, имеющей уравнение y=f(x), где f(x) – положительная и непрерывная в промежутке [a,b] функция: снизу она ограничена отрезком AB оси x, с боков – двумя ординатами AD и BC. С целью нахождения площади разобьем промежуток [a,b] на части:

Обозначив через и , соответственно, наименьшее и наибольшее значение функции F(x) в i-м промежутке (i=0,1,…,n-1), составим суммы Дарбу:

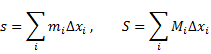
Они представляют собой площади ступенчатых фигур, составленных из входящих и выходящих треугольников, поэтому s<P<S. Но при стремлении к нулю наибольшей из разностей обе суммы имеют своим пределом интеграл , следовательно, ему и равна искомая площадь

Если криволинейная трапеция CDFE ограничена и снизу и сверху кривыми, уравнения которых то, рассматривая её как разность двух фигур ABFE и ABDC, получим площадь названной трапеции в виде

10.Ограниченность интегрируемой функции на отрезке.

Теорема. Если функция интегрируема на некотором отрезке, то она ограничена на этом отрезке.

Доказательство. Пусть функция f не ограничена на отрезке [a,b] и пусть фиксировано некоторое разбиение этого отрезка. В силу неограниченности функции f на всём отрезке [a,b] она не ограничена по крайней мере на одном отрезке разбиения τ. Пусть для определенности функция f не ограничена на отрезке [x0, x1], тогда на этом отрезке существует последовательность [x0, x1], n=1,2… такая что (1). Зафиксируем теперь каким-либо образом точки ξiЄ[xi-1,xi], i=2,3,…,k, тогда сумма будет иметь определённое значение. Поэтому в силу (1) 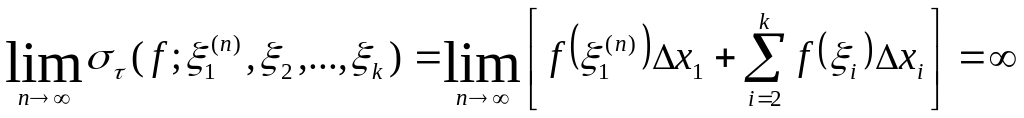, и, значит, каково бы ни было число M>0, всегда можно подобрать такой номер n0, что если на первом отрезке [x0, x1] взять точку , то >M. Отсюда следует, что суммы στ не могут стремиться ни к какому пределу при δτ → 0. Теорема доказана.

11.Независимость интеграла Римана от значения подынтегральной функции в конечном числе точек.

Пусть f(x) интегрируема на a,b. Если её изменить в конечном числе точек, то она останется интегрируемой, и интеграл не изменится. Т.е. если

То:

1) - интеграл по Риману

2)

Док-во:

=>

12.Интеграл по объединению отрезков.

Если функция f интегрируема на отрезке [a,b], то она интегрируема и на любом отрезке

Док-во:

Если - какое-либо разбиение отрезка , то всегда, добавив к нему соответствующее конечное множество точек, лежащих на отрезка [a,b], можно получить разбиение отрезка [a,b] той же мелкости

Обозначив посредством и колебания функции f соответственно на отрезках и и заметив, что отличается от , на неотрицательные слагаемые вида , соответствующие отрезкам разбиения T, лежащим вне отрезка , получим

Вытекает, что , поэтому , а это означает интегрируемость ф-ции f на отрезке

13.Суммы Дарбу. Свойства сумм Дарбу.

Обозначим через и точную нижнюю и верхнюю границы функции f(x) в i-м промежутке и составим суммы

Эти суммы носят название, соответственно, нижней и верхней интегральных сумм, или сумм Дарбу.

Суммы Дарбу обладают следующими свойствами: 1. Каждая нижняя сумма Дарбу не превосходит любой верхней:

(T1 b T2 – Разбиения отрезка [a,b]).

Док-во: Пусть - разбиения отрезка [a,b],

. Условие означает, что каждый отрезок разбиения T является объединением некоторых отрезков разбиения , обозначим эти отрезки , тогда , где суммирование ведется по всем таким индексам , что .Отсюда следует, что .

Выполняются неравенства ,

2.Нижняя (Верхняя) сумма Дарбу является нижней (верхней) гранью интегральных сумм Римана, соответствующих данному разбиению

3.Имеет место равенство

14.Признак интегрируемости (существования интеграла Римана) в терминах сумм Дарбу

Теорема 1: Для того, чтобы ограниченная на некотором отрезке функция была интегрируема на нем, необходимо и достаточно, чтобы разность верхних и нижних сумм Дарбу стремилась к нулю, когда мелкость разбиений отрезка стремиться к нулю:

Где – разбиение отрезка [a,b], а - колебание функции f на отрезке .

Док-во: Необходимость: Пусть ограниченная на отрезке [a,b] функция f интегрируема на этом отрезке и . Тогда . Поэтому для любого существует такое , что, каковы бы ни были разбиение отрезка [a,b], имеющие мелкость , и точки , k=1,2,…., , для интегральной суммы выполняется неравенство , а, следовательно и неравенство

Переходя в неравенстве к нижней и верхней граням относительно точек , в силу свойств сумм Дарбу получим

Таким образом, если , то . Отсюда следует, что

Достаточность: Пусть ф-ция F ограничена на отрезке [a,b] и для её сумм Дарбу выполняется условие .Из определения нижнего и верхнего интегралов и неравенства имеем

Поэтому . Отсюда в силу условия (1) следует, что . Обозначим общее значение нижнего и верхнего интегралов через I, т.е. . Из (2) будем иметь , но любая интегральная сумма также лежит между суммами Дарбу и , поэтому . Отсюда в силу условия (1) следует, что . Это означает, что существует предел интегральных сумм

Ф-я интегрируема, причем

15. Интегрируемость любой монотонной функции на отрезке.

Теорема: Функция, монотонная на отрезке, интегрируема на нем.

Пусть для определенности функция f возрастает на отрезке [a,b]. Тогда, в частности, для любого выполняется неравенство

И, следовательно, функция f ограничена на отрезке [a,b]. Очевидно, также, что в силу возрастания функции F для любого разбиения отрезка [a,b] имеют место равенства

Заметив, что

И что , получим

Отсюда следует, что и, поэтому, функция f интегрируема на отрезке [a,b].

16. Признак интегрируемости в терминах колебания функции на отрезках разбиения

Если ф-я f интегрируема на отрезке [a,b], а и - ее суммы Дарбу, то

Для того, чтобы ограниченная на отрезке [a,b] функция f была на нем интегрируема, необходимо и достаточно, чтобы

Док-во: По теореме Дарбу:

17. Равномерная непрерывность функции на множестве. Теорема Кантора о равномерной непрерывности функции на отрезке.

Определение: Функция f, заданная на множестве {x} называется равномерно непрерывной на нем, если для любого существует такое , что для любых двух точек таких, что , выполняется неравенство .

В символической записи определение непрерывности:

Определение равномерной непрерывности:

Здесь точки x и x’ принадлежат множеству, на котором задана функция f.

Теорема Кантора о равномерной непрерывной функции на отрезке:

Функция, непрерывная на отрезке, равномерно непрерывна на нем.

Док-во:

Предположим, что существует непрерывная на отрезке [a,b] функция f, которая на нем не равномерно непрерывна. Это означает, что найдутся такие точки , что , но . В частности, для найдутся такие точки, обозначим их , что

Но

Из последовательности точек можно выделить сходящуюся последовательность , обозначим её предел :

Поскольку , то . Функция f непрерывна в точке , поэтому

Подпоследовательность подпоследовательности также сходится в точке , ибо

При . Поэтому

Отсюда следует

А это противоречит условию, что