1. Тригонометрическая форма

Любой периодический сигнал x(t), удовлетворяющий условию Дирихле (x(t) – ограниченая, кусочно-непрерывная, имеет на протяжении периода конечное число экстремумов), может быть представлен в виде ряда Фурье по тригонометрическим функциям:

(1.1)

Это выражение указывает на то, что периодическая функция x(t), имеющая период Т может быть разложена по sin и cos углов, кратных углу .

Е сли период функции x(t) равен Т, то основная круговая частота будет , тогда в формуле разложения x(t) значения коэффициентов a₀, a_k, b_k определяется формулами:

k= 1, 2, 3

Зная коэффициенты a_k и b_k , можно определить значения амплитуды и начальной фазы  k-й гармоники.

(1.5) (1.6)

Для практического анализа частотных свойств применяется формула (1.7), так как показывает, какой частоте сигнала соответствует определенная амплитуда

(1.7), где - постоянная составляющая функции x(t);

k-я гармоническая составляющая; - амплитуда, частота и начальная фаза k-й гармонической составляющей; - частота основной гармоники;

Т- период колебаний.

2. Комплексная форма

В математическом отношении удобнее оперировать комплексной формой ряда Фурье. Её получают, применяя преобразование Эйлера

(1.8); (1.9)

Комплексная форма имеет вид: (1.10); где (1.11)

является комплексной амплитудой k-й гармоники для k=0, 2, 3,…

Формулы (1.10) и (1.11) именуются парой преобразования Фурье. Формула (1.10) даёт временное описание сигнала x(t), если известны комплексные амплитуды C_k её гармонических составляющих. Совокупность операций, в результате выполнения которых могут быть определены гармоники периодической функции x(t), называется гармоническим анализом.

3. Определение погрешности

При разложении периодических функций на сумму гармоник на практике часто ограничиваются несколькими первыми гармониками, а остальные не учитываются. Приближенно представляя функцию x(t) с помощью тригонометрического многочлена вида

(1.12) можно получить большую или меньшую ошибку представления в зависимости от способа выбора коэффициентов многочлена . Оценить величину ошибки наиболее удобно с помощью средней квадратичной погрешности , определяемой для периодической функции x(t) с периодом T=2 равенством:

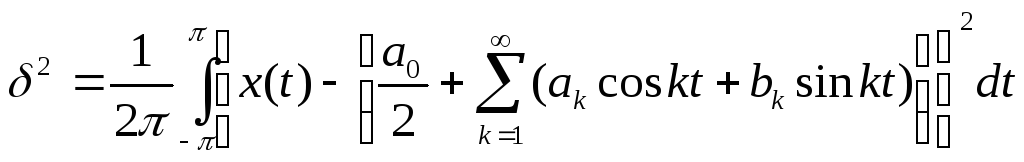(1.13)

4. Спектр

Совокупности коэффициентов a_k, b_k, k=1, 2, 3,…, разложения периодической функции x(t) в ряд Фурье называется частотными спектрами этой функции.

Совокупность амплитуд и соответствующих частот гармоник принято называть спектром амплитуд.

Совокупность амплитуд и соответствующих частот гармоник называется спектром фаз.

Спектр амплитуд и спектр фаз однозначно определяют сигнал. Однако для многих практических задач достаточно ограничиться спектром амплитуд.

A_k _k

спектральные линии

0 0

₀ 2₀ 3₀ k₀ ₀ 2₀ k₀

Характерной особенностью спектра периодического сигнала является его прерывистость (дискретность). Расстояние между соседними спектральными линиями одинаковое и равно частоте основной гармоники.

Б) Непериодические сигналы

Всякий непериодический сигнал можно рассматривать как периодический, период изменения которого равен . В связи с этим спектральный анализ периодических процессов может быть обобщен и на непериодический сигнал.

x(t)

0 t

Любой физически реализуемый сигнал с конечной энергией обязательно ограничен во времени, или, иными словами, функция, изображающая такой сигнал, абсолютно интегрируема. В связи с этим непериодический сигнал может быть выражен модифицированной формулой периодического сигнала. Модификация заключается в приравнивании периода колебаний Т бесконечности и следующих из этого математических преобразований. Подставляя в комплексную форму ряда Фурье функции выражение комплексной амплитуды , получим:

(2.1) , где

Для непериодической функции , следовательно, частотный интервал между соседними гармониками . В этом выражении деление на бесконечно большой период Т может быть заменено умножением на бесконечно малое приращение частоты , что в свою очередь, превращает процесс суммирования в интегрирование, а произведение в текущую частоту

то есть: (2.2) Это выражение известно как двойной интеграл Фурье, а величина (2.3) называется прямым преобразованием Фурье функции . Эта величина характеризует спектральный состав непериодической функции и может быть названа спектральной плотностью или спектральной характеристикой функции .

Выражение (2.4) представляющее зависимость непериодической функции от её спектральной характеристики, называется обратным преобразованием Фурье.

Здесь: - спектральная плотность; - амплитудно-частотная характеристика сигнала; - фазо-частотная характеристика сигнала .

Представление непериодической функции интегралом Фурье возможно при выполнении следующих условий:

1. функция удовлетворяет условиям Дирихле

2. функция абсолютно интегрируема, т.е.

(2.5)(этим условиям удовлетворяет практически любой реальный сигнал).

Огибающая спектра (модуль спектральной плотности) непериодической функции (сигнала) имеет непрерывный характер.

Т.е. спектр непериодического сигнала в отличие от спектра периодического сигнала является сплошным. Спектральная плотность однозначно отображает непериодический сигнал и удовлетворяет условиям:

1. ;

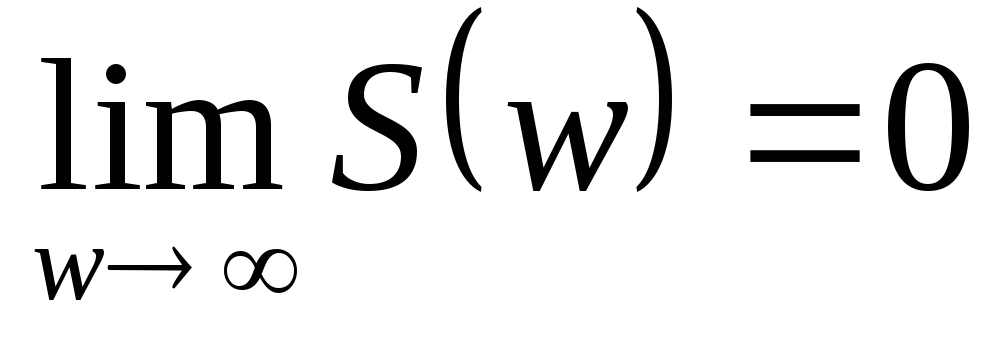2. Модуль спектральной плотности является четной, а аргумент – нечетной функцией частоты, т.е. ,

S(w) φ(w)

φ(w)

S(w)

-w w

0