Тема 5.2. Внешний фотоэффект. Внешний фотоэффект. – это явление вырывания электронов из твердых и жидких тел под действием света.

Уравнение Эйнштейна для внешнего фотоэффекта. 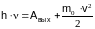.Здесь – постоянная Планка, – частота, 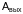– работа выхода электрона из металла, 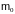– масса покоя электрона, v – скорость электрона.

Эффект Комптона.  рассеяние эл--магн. волны на свободном электроне, сопровождающееся уменьшением частоты. Эффект наблюдается для больших частот рассеиваемого эл--магн. излучения (в рентг. области и выше). Он проявлялся уже в первых опытах по рассеянию рснтг; лучей на свободных электронах, но впервые с требуёмой тщательностью был изучен А. Комп-тоном (A. Compton) в 1922-23. Исторически К. э. явился одним из гл. свидетельств в пользу корпускулярной природы эл--магн. излучения (в частности, света). С точки зрения классич. электродинамики рассеяние с изменением частоты невозможно.Элементарная теория эффекта была дана А. Комп-тоном и независимо от него П. Дебаем (P. Debye) на основе представления о том, что рентг. излучение состоит из фотонов .Для объяснения эффекта приходилось предположить, что фотон обладает как энергией   , так и импульсом   (здесь v и  - частота и длина волны света, п - единичный вектор в направлении распространения волны).

Фотон, его масса, энергия и импульс. Согласно гипотезе световых квантов Эйнштейна, свет испускается, поглощается и распространяется дискретными порциями (квантами), названными фотонами.Энергия фотона ₀=h. Его масса находится из закона взаимосвязи массы и энергии (см. (40.8)):

                                                              

Фотон — элементарная частица, которая всегда (в любой среде!) движется со скоро­стью света с и имеет массу покоя, равную нулю. Следовательно, масса фотона отличается от массы таких элементарных частиц, как электрон, протон и нейтрон, которые обладают отличной от нуля массой покоя и могут находиться в состоянии покоя.Импульс фотона р_ получим, если в общей формуле (40.7) теории относительностиположим массу покоя фотона  = 0:

   Из приведенных рассуждений следует, что фотон, как и любая другая частица, характеризуется энергией, массой и импульсом. Выражения (205.1), (205.2) и (200.2) связывают корпускулярные характеристики фотона — массу, импульс и энергию — с волновой характеристикой света — его частотой.Если фотоны обладают импульсом, то свет, падающий на тело, должен оказывать на него давление.Согласно квантовой теории, давление света на поверхность обусловлено тем, что каждый фотон при соударении с поверхностью передает ей свой импульс.Рассчитаем с точки зрения квантовой теории световое давление, оказываемое на поверхность тела потоком монохроматического излучения (частота ), падающего перпендикулярно поверхности. Если в единицу времени на единицу площади поверхности тела падает N фотонов, то при коэффициенте отражения света от поверхности тела N фотонов отразится, а (1–)N — поглотится. Каждый поглощенный фотон передаст поверхности импульс p_=h/c, а каждый отраженный — 2p_=2h/c (при от­ражении импульс фотона изменяется на –p_). Давление света на поверхность равно импульсу, который передают поверхности в 1 с N фотонов:

Nh=E_e есть энергия всех фотонов, падающих на единицу поверхности в единицу времени, т. е. энергетическая освещенность поверхности, a E_e/c=w — объ­емная плотность энергии излучения. Поэтому давление, производимое светом при нормальном падении на поверхность,

          

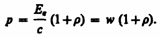
Корпускулярно – волновой дуализм материи КОРПУСКУЛЯРНО-ВОЛНОВОЙ дуализм, заключается в том, что любые микрочастицы материи (фотоны, электроны, протоны, атомы и другие) обладают свойствами и частиц (корпускул) и волн. Количественное выражение корпускулярно-волнового дуализма - соотношение, введенное в 1924 Л. де Бройлем (смотри Волны де Бройля). Корпускулярно-волновой дуализм получил объяснение в квантовой механике.. Гипотеза де-Бройля.  Если фотон обладает энергией  и импульсом  , то и частица (например электрон), движущаяся с некоторой скоростью, обладает волновыми свойствами, т.е.движение частицы можно рассматривать как движение волны.Согласно квантовой механике, свободное движение частицы с массой m и импульсом  (где υ – скорость частицы) можно представить как плоскую монохроматическую волну  (волну де Бройля) с длиной волны альфа=h\pВ 1924 г. Луи де-Бройль выдвинул смелую гипотезу, что дуалн-зм не является особенностью одних только оптических явлений, но имеет универсальное значение.

Тема 5.3. Квантово-механическое описание микромира. Принцип дополнительности Бора. Принцип дополнительности — методологический принцип, сформулированный Нильсом Бором применительно к квантовой физике, согласно которому, для того чтобы наиболее адекватно описать физический объект, относящийся к микромиру, его нужно описывать во взаимоисключающих, дополнительных системах описания, например одновременно и как волну, и как частицу (ср. многозначные логики ). Принцип неопределенности.  — фундаментальное неравенство (соотношение неопределённостей), устанавливающее предел точности одновременного определения пары характеризующих квантовую систему физических наблюдаемых (см. физическая величина),

описываемых некоммутирующими операторами (например,координаты и импульса, тока и напряжения, электрического и магнитного поля). Соотношение неопределенностей^{[* 1]} задаёт нижний предел для произведения среднеквадратичных отклонений пары квантовых наблюдаемых. Принцип неопределённости, открытыйВернером Гейзенбергом в 1927 г., является одним из краеугольных камней квантовой механики. Волновая функция и ее физический смысл. Из содержания предыдущих двух параграфов следует, что с микрочастицей сопоставляют волновой процесс, который соответствует ее движению, поэтому состояние частицы в квантовой механике описывают волновой функцией, которая зависит от координат и времени (x,y,z,t). Конкретный вид -функции определяется состоянием частицы, характером действующих на нее сил. Если силовое поле, действующее на частицу, является стационарным, т.е. не завися­щим от времени, то -функцию можно представить в виде произведения двух сомножителей, один из которых зависит от времени, а другой  – откоординат:

             (3.1)

В дальнейшем будем рассматривать только стационарные состояния. -функция является вероятностной характеристикой состояния частицы. Чтобы пояснить это, мысленно выделим достаточно малый объем  , в пределах которого значения -функции будем считать одинаковыми. Тогда вероятность нахождения dW частицы в данном объ­еме пропорциональна ему и зависит от квадрата модуля-функции (квадрата модуля амплитуды волн де Бройля):                             

                                     (3.2)

Отсюда следует физический смысл волновой функции:

.                                              (3.3)

Квадрат модуля волновой функции имеет смысл плотности вероят­ности, т.е. определяет вероятность нахождения частицы в единичном объеме в окрестности точки с координатами х, у, z.

Интегрируя выражение (3.2) по объему, определяем вероятность нахождения частицы в этом объеме в условиях стационарного поля:

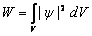                                               (3.4)

Если известно, что частица находится в пределах объема V, то инте­грал выражения (3.4), взятый по объему V, должен быть равен единице: 

                                                         (3.5)

– условие нормировки -функции.

Чтобы волновая функция являлась объективной характеристикой со­стояния микрочастиц, она должна быть конечной, однозначной, непре­рывной, так как вероятность не может быть больше единицы, не может быть неоднозначной величиной и не может изменяться скачками. Таким образом, состояние микрочастицы полностью определяется волновой функцией. Частица может быть обнаружена в любой точке пространства, в которой волновая функция отлична от нуля.

Стационарные состояния. В квантовой физике стационарным состоянием атома называют состояние, при котором оно имеет постоянную энергию. Уравнение Шредингера для стационарных состояний. В развитие идеи де Бройля о волновых свойствах частиц Шредингер в 1926 г. получил уравнение

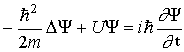 (20)где m - масса частицы,   - мнимая единица, U - потенциальная энергия частицы,  - оператор Лапласа [ см. (1.10)].Решение уравнения Шредингера позволяет найти волновую функцию (x, y, z, t) частицы, которая описывает микросостояние частицы и ее волновые свойства.Если поле внешних сил постоянно во времени (т.е. стационарно), то U не зависит явно от t. В этом случае решение уравнения (20) распадается на два множителяx, y, z, t) =(x, y, z) exp[-i(E/ )t] (21)где E/ =.В стационарном случае уравнение Шредингера имеет вид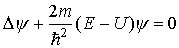

 (22)

где Е, U - полная и потенциальная энергия, m - масса частицы.Следует заметить, что исторически название "волновой функции" возникло в связи с тем, что уравнение (20) или (22), определяющее эту функцию, относится к виду волновых уравнений.