Тема 3.3. Магнитное поле в вакууме. Магнитное поле– это особая форма материи.Магнитное поле – порождается любыми движущимися зарядами: электрический ток в металле, в электролите, в газе, пучок электронов, протонов и т.п.Индукция магнитного поля-это силовая характеристика магнитного поля. Вектор магнитной индукции направлен всегда так, как сориентирована свободно вращающаяся магнитная стрелка в магнитном поле.Единица измерения магнитной индукции в системе СИ:

Сила Лоренца- сила, с которой, в рамках классической (не-квантовой) физики, электромагнитное поле действует на заряженную частицу (точечную, в общем случае - движущуюся).Выражение для силы Ампера можно записать в виде: 

F = q n S Δl υB sin α.

Так как полное число N носителей свободного заряда в проводнике длиной Δl и сечением S равно n S Δl, то сила, действующая на одну заряженную частицу, равна 

FЛ = q υ B sin α.

Движение заряженных частиц в магнитном поле. Формула силы Лоренца дает возможность найти ряд закономерностей движения заряженных частиц в магнитном поле. Зная направление силы Лоренца и направление вызываемого ею отклонения заряженной частицы в магнитном поле можно найти знак заряда частиц, которые движутся в магнитных полях. Для вывода общих закономерностей будем полагать, что магнитное поле однородно и на частицы не действуют электрические поля. Если заряженная частица в магнитном поле движется со скоростью v вдоль линий магнитной индукции, то угол α между векторами v и Вравен 0 или π. Тогда сила Лоренца равна нулю, т. е. магнитное поле на частицу не действует и она движется равномерно и прямолинейно. В случае, если заряженная частица движется в магнитном поле со скоростью v, которая перпендикулярна вектору В, то сила ЛоренцаF=Q[vB] постоянна по модулю и перпендикулярна к траектории частицы. По второму закону Ньютона, сила Лоренца создает центростремительное ускорение. Значит, что частица будет двигаться по окружности, радиус r которой находится из условия QvB=mv²/r , следовательно  Период вращения частицы, т. е. время Т, за которое она совершает один полный оборот,    т. е. период вращения частицы в однородном магнитном поле задается только величиной, которая обратна удельному заряду (Q/m) частицы, и магнитной индукцией поля, но при этом не зависит от ее скорости (при v<<c). На этом соображении основано действие циклических ускорителей заряженных частиц. В случае, если скорость v заряженной частицы направлена под углом α к вектору В (рис. 170), то ее движение можно задать в виде суперпозиции: 1) прямолинейного равномерного движения вдоль поля со скоростью v_parall=vcosα ; 2) равномерного движения со скоростью v_perpend=vsinα по окружности в плоскости, которая перпендикулярна полю. Радиус окружности задается формулой (1) (в этом случае надо вместо v подставить v_perpend=vsinα). В результате сложения двух данных движений возникает движение по спирали, ось которой параллельна магнитному полю (рис. 1). Шаг винтовой (спиральной) линии   Направление, в котором закручивается спираль, определяется знаком заряда частицы.  Если скорость v заряженной частицы составляет угол α с направлением вектора В неоднородного магнитного поля, у которого индукция возрастает в направлении движения частицы, то r и h уменьшаются с увеличением В. На этом основана фокусировка заряженных частиц в магнитном поле. 

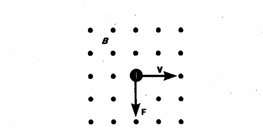
Магнитное поле движущегося заряда.

Любой проводник с током создает в окружающем пространстве магнитное поле. При этом электрический же ток является упорядоченным движением электрических зарядов. Значит можно считать, что любой движущийся в вакууме или среде заряд попрождает вокруг себя магнитное поле. В результате обобщения многочисленных опытных данных был установлен закон, который определяет поле В точечного заряда Q, движущегося с постоянной нерелятивистской скоростью v. Этот закон задается формулой  где r — радиус-вектор, который проведен от заряда Q к точке наблюдения М (рис. 1). Согласно (1), вектор В направлен перпендикулярно плоскости, в которой находятся векторы v и r : его направление совпадает с направлением поступательного движения правого винта при его вращении от v к r.  Рис.1 Модуль вектора магнитной индукции (1) находится по формуле  где α — угол между векторами v и r.  Сопоставляя закон Био-Савара-Лапласа и (1), мы видим, что движущийся заряд по своим магнитным свойствам эквивалентен элементу тока:  Приведенные законы (1) и (2) выполняются лишь при малых скоростях (v<<с) движущихся зарядов, когда электрическое поле движущегося с постоянной скорость заряда можно считать электростатическим, т. е. создаваемым неподвижным зарядом, который находится в той точке, где в данный момент времени находится движущийся заряд. Формула (1) задает магнитную индукцию положительного заряда, движущегося со скоростью v. При движении отрицательнго заряда Q заменяется на -Q. Скорость v - относительная скорость, т. е. скорость относительно системы отсчета наблюдателя. Вектор В в данной системе отсчета зависит как от времени, так и от расположения наблюдателя. Поэтому следует отметить относительный характер магнитного поля движущегося заряда.Первый, кто обнаружил поле движущегося заряда, был американский физик Г. Роуланду (1848—1901). Окончательно этот факт был установлен профессором Московского университета А. А. Эйхенвальдом (1863—1944), который изучал магнитное поле конвекционного тока и магнитное поле связанных зарядов поляризованного диэлектрика. Магнитное поле движущихся с постоянной скоростьб зарядов было измерено академиком А. Ф. Иоффе, который также доказал эквивалентность, в смысле возбуждения магнитного поля, электронного пучка и тока проводимости.

Принцип суперпозиции:магнитное поле, создаваемое совокупностью движущихся зарядов, равно векторной

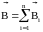
сумме полей, создаваемых отдельными зарядами , где 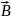- магнитная индукция результирующего поля, - магнитная индукция полей, создаваемых отдельными зарядами.

Закон Био-Савара-Лапласа для проводника с током I, элемент dl которого создает в некоторой точке А (рис. 1) индукцию поля dB, равен  где dl - вектор, по модулю равный длине dl элемента проводника и совпадающий по направлению с током, r - радиус-вектор, который проведен из элемента dl проводника в точку А поля, r - модуль радиуса-вектора r. Направление dB перпендикулярно dl и r, т. е. перпендикулярно плоскости, в которой они лежат, и совпадает с направлением касательной к линии магнитной индукции. Это направление может быть найдено по правилу правого винта: направление вращения головки винта дает направление dB, если поступательное движение винта совпадает с направлением тока в элементе.  Модуль вектора dB задается выражением  где α — угол между векторами dl и r. 

Магнитное поле прямолинейного проводника с током. Для получения спектра магнитного поля прямого проводника с током проводник пропускают сквозь лист картона. На картон насыпают тонкий слой железных опилок, и опилки слегка встряхивают. Под действием магнитного поля железные опилки располагаются по концентрическим окружностям. По касательным к ним расположатся и магнитные стрелки вокруг такого проводника с током.Таким образом, линии магнитной индукции магнитного поля прямолинейного тока представляют собой концентрические окружности, расположенные в плоскости, перпендикулярной к проводнику, с центром на оси проводника. Направление линий индукции определяется правилом правого винта: если поворачивать головку винта так, чтобы поступательное движение острия винта происходило вдоль тока в проводнике, то направление вращения головки указывает направление линий магнитной индукции поля прямого проводника с током.Магнитное поле кругового тока.Определим магнитную индукцию на оси проводника с током на расстоянии х от плоскости кругового тока. Векторы    перпендикулярны плоскостям, проходящим через соответствующие    и   . Следовательно, они образуют симметричный конический веер. Из соображения симметрии видно, что результирующий вектор    направлен вдоль оси кругового тока. Каждый из векторов    вносит вклад равный  , а    взаимно уничтожаются. Но  ,  , а т.к. угол между    и    α – прямой, то    тогда получим

,

Подставив в (1.6.1)    и, проинтегрировав по всему контуру  , получим выражение для нахождения магнитной индукции кругового тока:

,

(1.6.2)

При  , получим магнитную индукцию в центре кругового тока:

,

(1.6.3)

 Заметим, что в числителе (1.6.2)      – магнитный момент контура. Тогда, на большом расстоянии от контура, при  , магнитную индукцию можно рассчитать по формуле:

,

Теорема о циркуляции вектора напряженности (индукции) магнитного поля. Теорема о циркуляции вектора В.

Поскольку магнитное поле создается токами, а ненулевая циркуляция означает, что косинус угла между вектором поля и векторами перемещений преимущественно не меняет знак (т. е. перемещения происходят преимущественно вдоль или против силовых линий), то в этом случае замкнутый контур обхода пронизывают создающие поле, направленное вдоль (или против) направления обхода, токи, алгебраическая сумма которых не равна нулю. Ток считается положительным, если его направление связано с направлением обхода правилом правого винта:

Циркуляция вектора индукции магнитного поля прямопропорциональна алгебраической сумме пронизывающих контур токов; коэффициентом пропорциональности служит магнитная постоянная, умноженная на магнитную проницаемость  среды, которая в результате намагничивания в   раз изменяет результирующее поле:

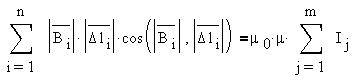
Циркуляцией вектора В по заданному замкнутому контуру называется интеграл где dl — вектор элементарной длины контура, направленной вдоль обхода контура, B_l=Bcos — составляющая вектора В в направлении касательной к контуру (с учетом выбранного направления обхода),  — угол между векторами В и dl.

Поле тороида и соленоида. Найдем с помощью теоремы о циркуляции, индукцию магнитного поля внутри соленоида. Рассмотрим соленоид длиной l, который имеет N витков, и по которому течет ток (рис. 1). Будем считать длину соленоида во много раз больше, чем диаметр его витков. Экспериментальное изучение магнитного поля соленоида (см. главу "магнитное поле и его характеристики") показывает, что внутри соленоида поле однородно, вне соленоида — неоднородно и практически отсутствует. На рис. 1 даны линии магнитной индукции внутри и вне соленоида. Чем соленоид длиннее, тем магнитная индукция вне его меньше. Поэтому приближенно можно полагать, что поле бесконечно длинного соленоида сосредоточено целиком внутри него, а поле соленоида можно не учитывать. Для вычисления магнитной индукции В выберем замкнутый прямоугольный контур ABCDA, как показано на рис. 1. Циркуляция вектора Впо замкнутому контуру ABCDA, который охватывает все N витков, используя формулу циркуляции вектора В, будет    Интеграл по ABCDA можно разложить на четыре интеграла: по АВ, ВС, CD и DA. На участках АВ и CD контур и линии магнитной индукции перпендикулярны: B_l=0. На участке вне соленоида B=0. На участке DA циркуляция вектора В равна В_l (контур и линии магнитной индукции совпадают); значит,   (1) 

Из (1) приходим к формуле магнитной индукции поля внутри соленоида (в вакууме):   (2)  Мы видим, что поле внутри соленоида однородно (при расчетах пренебрегают краевыми эффектами в областях, прилегающих к торцам соленоида). Но отметим, что вывод этой формулы не совсем корректен (поскольку линии магнитной индукции замкнуты, и интеграл по внешнему участку магнитного поля строго нулю не равен). Корректно найти поле внутри соленоида можно, используя закон Био — Савара — Лапласа; в результате получается такая же формула (2). Важное практическое значение имеет также магнитное поле тороида — кольцевой катушки, у которой витки намотаны на сердечник, который имеет форму тора (рис. 2). Магнитное поле, как известно из опыта, сосредоточено внутри тороида, а вне его поле равно нулю.  В данном случае линии магнитной индукции, как следует из соображений симметрии, есть окружности, у которых центры расположены по оси тороида. В качестве контура возьмем одну такую окружность радиуса r. Тогда, используя теорему о циркуляции, B•2πr=μ₀NI, откуда следует, что магнитная индукция внутри тороида (в вакууме)  где N — число витков тороида. 

Если контур проходит вне тороида, то токов он не охватывает и B•2πr = 0. Следовательно, что поле вне тороида отсутствует (что показывает и опыт).  Сила Ампера. Сила, с которой магнитное поле действует на помещенный в него проводник с током, называется силой Ампера.Величина этой силы, действующей на элемент Δl проводника с током I в магнитном поле с индукцией   , определяется законом Ампера:

 , (1)

где α – угол между направлениями тока и вектора индукции.Направление силы Ампера можно найти с помощью правила левой руки: если левую руку расположить так, чтобы линии магнитной индукции входили в ладонь, а четыре вытянутых пальца совпадали по направлению с направлением тока, то отогнутый на 90° большой палец укажет направление силы, действующей на элемент проводника.

Взаимодействие параллельных токов. Закон Ампера используется при нахождении силы взаимодействия двух токов. Рассмотрим два бесконечных прямолинейных параллельных тока I₁ и I₂; (направления токов даны на рис. 1), расстояние между которыми R. Каждый из проводников создает вокруг себя магнитное поле, которое действует по закону Ампера на соседний проводник с током. Найдем, с какой силой действует магнитное поле тока I₁ на элемент dl второго проводника с током I₂. Магнитное поле тока I₁ есть линии магнитной индукции, представляющие собой концентрические окружности. Направление вектора B₁ задается правилом правого винта, его модуль по формуле (5) есть  Направление силы dF₁, с которой поле B₁ действует на участок dl второго тока, находится по правилу левой руки и указано на рисунке. Модуль силы, используя (2), с учетом того, что угол α между элементами тока I₂ и вектором B₁ прямой, будет равен  подставляя значение для В₁, найдем   (3)  Аналогично рассуждая, можно показать, что сила dF₂ с которой магнитное поле тока I₂ действует на элемент dl первого проводника с током I₁, направлена в противоположную сторону и по модулю равна   (4)  Сопоставление выражений (3) и (4) дает, что  т. е. два параллельных тока одинакового направления притягиваются друг к другу с силой, равной   (5)  Если токи имеют противоположные направления, то, используя правило левой руки, определим, что между ними действует сила отталкивания, определяемая выражением (5). Магнитный поток. - поток Ф вектора магнитной индукции В через к.-л. поверхность S:

Здесь dS - элемент площади, п - единичный вектор нормали к S. В СИ М. п. измеряется в веберах (Во), в гауссовой системе единиц (к-рая применяется ниже) - в максвеллах (Мкс); 1 Вб=10⁸ Мкс. Поскольку вектор В является чисто вихревым  , М. п. через произвольную замкнутую поверхность S равен нулю. Это свойство, установленное Гауссом, может нарушаться только при наличии внутри S магнитных монополей, пока ещё гипотетических.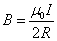