Билет 10

Нормальное распределение. Его порождает интеграл Пуассона:

I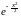 dx .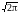

Докажем это равенство. Интеграл бы легко вычислялся, если бы подынтегральное выражение содержало множитель x. Такой множитель можно ввести под знак интеграла с помощью следующего остроумного приёма.

Запишем квадрат интеграла в следующем виде:

I² dx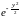 dy,

а теперь представим произведение интегралов как двойной интеграл:

I²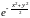 dxdy.

Перейдём в этом интеграле к полярным координатам. Положим: xrcos, y rsin, и ещё вспомним, что абсолютная величина якобиана при переходе от декартовых координат к полярным равна r. Заметим, наконец, что областью интегрирования двойного интеграла является вся плоскость, так что границы изменения переменных r и , соответственно, таковы: r[0; ), [0; 2). Поэтому:

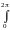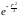I² d rdr.

Теперь легко убедиться, что 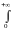rdr1, а потому I²2.

Распределение с плотностью

p(x)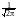 , x(; )

называется стандартным нормальным законом и обозначается N(0, 1).

Ему соответствует функция распределения:

F₀(x) dx.

Обычно принято табулировать интеграл

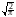
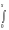(x) dx,

называемый интегралом ошибок или интегралом Лапласа. Функция распределения стандартного нормального закона просто выражается через этот интеграл:

F₀(x)  (x).

Если в интеграл Пуассона ввести параметры масштаба и сдвига с помощью замены переменной, заменив x на 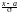, то он примет вид:

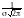
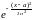dx1.

Случайную величину с плотностью вероятности

p(x) , x(; ),

называют нормально распределённой случайной величиной или просто нормальной. Соответствующий ей закон распределения обозначают N(a, ), a и  – параметры распределения (0, a – любое вещественное число).

График p(x) представлен на рис. 1.

p(x) O x a Рис. 1.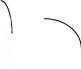

a – точка максимума p(x), его значение равно . Так как площадь под кривой всегда равна единице, то чем меньше , тем больше вероятности сосредоточивается вблизи максимума. Таким образом, устанавливаем вероятностный смысл параметров нормального закона: областью наиболее вероятных значений нормальной случайной величины является окрестность точки a, а  указывает на степень концентрации вероятности в окрестности точки a – чем меньше , тем менее вероятны заметные отклонения X от a.

Функцию распределения произвольного нормального закона легко выразить через интеграл Лапласа. Для этого нужно в выражении для функции распределения

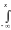F(x) dx

выполнить замену переменной, положив 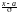y:

F(x) dy  ( ).

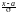Правило трёх сигм () — практически все значения нормально распределённой случайной величины лежат в интервале . Более строго — не менее чем с 99,7 % достоверностью значение нормально распределенной случайной величины лежит в указанном интервале (при условии, что величина истинная, а не полученная в результате обработки выборки).

Если же истинная величина неизвестна, то следует пользоваться не , а s. Таким образом, правило трёх сигм преобразуется в правило трёх s.