3. Прогнозное значение у. Интервалы прогноза по линейному уравнению регрессии.

4. Связь критериев Стьюдента и Фишера для парной регрессии.

Связь между F-критерием Фишера (при ) и t-критерием Стьюдента выражается равенством . Если t табл<t факт, то Но отклоняется, т.е. a,b, r не случайно отличаются от нуля и сформировались под влиянием систематически действующего фактора х. Если t табл>t факт, то гипотеза Но не отклоняется и признается случайная природа формирования a, b, r.

Билет 11

1. Проблема гетероскедастичности, способы их решения. Параметрические тесты Гольфельда-Кванта и Спирмена и их применение.

Проявление проблем гетероскед-сти можно предвидеть основываясь на знаниях характера данных. В этих случаях можно предпринимать действия на этапе спецификации модели регрессии. Это позволит уменьшить или устранить необходимость формальной проверки. В настоящее время используются следующие виды тестов гетероскед-сти, в которых делается предположение о наличие зависимости между дисперсией случайного члена и величиной объясняющей переменной:

1)Тест ранговой корреляции Спирмена.

При его выполнении предполагается, что дисперсия случайного члена будет либо увеличиваться, либо уменьшаться по мере увеличения X и поэтому в регрессии, оцениваемой с помощью метода наименьших квадратов абсолютные величины остатков и значение X будут коррелированны. Данные по X и остатки упорядочиваются, а затем определяется коэффициент ранговой корреляции: Ф(3.9),

Где Дi- разность между рангом X и рангом е, е- остатки(отклонение) фактических значений Y от теоретических значений.

2)Тест Голдфельда Квандта.

При проведении проверки по этому критерию предполагается, что дисперсия случайного члена пропорциональна значению X в этом наблюдении. Предполагается, что случайный член распределен нормально и не подвержен автокорреляции. Все наблюдения в выборке упорядочиваются по величине X, после чего оцениваются отдельные регрессии для первых n со штрихом наблюдений и для последних n со штрихом наблюдений. Если предположение о наличие гетероскед-сти верна, то дисперсия в последних n наблюдениях будет больше, чем в первых n со штрихом наблюдениях. Суммы квадратов остатков обозначают для первых n со штрихом наблюдений обозначают RSS1, для последних n со штрихом наблюдений RSS2, затем определяют их отношения. Это отношение имеет F-распределения при заданных (n со штрихом-k-1)/(n со штрихом-k-1) степенях свободы. Если n=30, то n со штрихом= min11.

2. Оценка надежности результатов множественной регрессии и корреляции.

3. Понятие коэффициента регрессии. Его значение для линейной и степенной зависимостей.

4. Значимость параметров уравнения регрессии. Критерий Стьюдента. Умение пользоваться таблицей.

Билет 12

1. Автокорреляция, как предпосылка МНК. Ее определение при построении регрессионной модели.

Оценка отсутствия автокорреляции остатков(т.е. значения остатков e_i распределены независимо друг от друга). Автокорреляция остатков означает наличие корреляции между остатками текущих и предыдущих (последующих) наблюдений. Коэффициент корреляции между e_i и e_j , где e_i — остатки текущих наблюдений, e_j — остатки предыдущих наблю­дений, может быть определен по обычной формуле линейного коэффициента корреляции . Если этот коэффициент окажется существенно отличным от ну­ля, то остатки автокоррелированы и функция плотности вероят­ности F(e) зависит j-й точки наблюдения и от распределения значений остатков в других точках наблюдения. Для регрессионных моделей по статической информации ав­токорреляция остатков может быть подсчитана, если наблюдения упорядочены по фактору х. Отсутствие автокорреляции остаточных величин обеспечива­ет состоятельность и эффективность оценок коэффициентов ре­грессии. Особенно актуально соблюдение данной предпосылки МНК при построении регрессионных моделей по рядам динами­ки, где ввиду наличия тенденции последующие уровни динами­ческого ряда, как правило, зависят от своих предыдущих уров­ней.

2. Отличие применения МНК к моделям нелинейным относительно исключаемых переменных и оцениваемых параметров.

3. Подбор линеаризующего преобразования. Тест Бокса-Кокса.

В эконометрике для оценки параметров нелинейных моделей используются два подхода:

линеаризация моделей, не линейных как по переменным, так и по параметрам, когда с помощью подходящих преобразований исходных переменных исследуемую зависимость представляют в виде линейного соотношения между преобразованными переменными;

методы нелинейной оптимизации на основе исходных данных (когда не удается подобрать соответствующее линеаризующее преобразование).

Пример Если необходимо оценить параметры не линейной по переменным регрессионной модели , то, вводя новые переменные , получим линейную модель: , параметры которой находятся обычным методом наименьших квадратов.

Нелинейность моделей по параметрам является более сложной проблемой. Непосредственное применение метода наименьших квадратов для их оценивания невозможно. К числу таких моделей относятся:мультипликативная (степенная) модель

экспоненциальная и другие.Эти модели могут быть приведены к линейным путем логарифмирования обеих частей уравнений. Тогда общий вид мультипликативной модели станет следующим:

К полученной модели уже можно применить МНК

4. Виды моделей, используемых в эконометрике. Какими методами осуществляется выбор вида математической функции у=f(x).

Для решения задач эк-ки существенным является использование матем. моделей. Они широко применяются в бизнесе, экономике, общ. науках, политич. процессах.

Матем. модели полезны для более широкого понимания происходящих процессов и их анализа. Модель, построенная на основе имеющихся значений объясн-х переменных, может быть использована для прогноза значений зависимой переменной в будущем.

Выделяют 3 соновн. класса моделей, к. применяются для анализа и прогноза.

1)Модели временных рядов.

К этому классу относится сл. модели: 1. Модель тренда (тенденция, развитие)

Y(t)= T(t) + E(t) (1.1)

Где T(t)-временной тренд заданного параметрич. вида

E(t)-случайная компонента

2. Модель сезонности

Y(t)= S(t) + E(t) (1.2)

Где S(t)-сезонная компонента

3.Модель тренда и сезонности:

А) аудитивная

Y(t)= T(t) + E(t) +S(t) (1,3)

Б) мультипликативная

Y(t)= T(t) E(t)S(t) (1.4)

К моделям временных рядов относится множество более сложных моделей, таких как модели адаптивного прогноза, модели авторегрессии, скользящей средней и т. д. Их общей чертой яв-ся то, что они объясн-т поведение временного ряда, исходя из его предыдущих значений.

2)Эконометрические модели (регрессионные модели с одним уравнением)

В таких моделях зависимая (объясняемая) величина y представлена в виде функции:

F(x,)=F(x₁ ,x₂,... x_к;₁,₂ ,…_к) (1.5.)Где х₁- х_к – независимая переменные ₁ - _к - параметры уравнения (коэффициенты)

В зависимости от вида функции модели делятся на линейные и нелинейные. Область применения таких моделей значительно шире, чем моделей времен. рядов.

3)Эконометрические модели (системы одновременных уравнений) Системы одновременных моделей. Эти модели описываются системами уравнений. Системы могут состоять из тождеств и регрессионных уравнений, каждое из которых может кроме объясн-х переменных включать в себя такие объясняемые переменные из др. уравнений системы, т. е. набор объясняемых переменных связан. между собой через уравнения систем. Данные модели исп-ся для характеристики страховой эк-ки.

Пусть Q_t^s – предложение товара в данный момент времени t, Q_t^D – спрос на товар в данный момент времени t, p_t – цена товара в момент времени t , у_t – доход в момент времени t. Тогда система уравнений «спрос-предложение» будет иметь сл. вид:

Q_t^s = а₁+ а₂р_t + а₃р_t-1+ E_t

Q_t^D = ₁ + ₂ р_t +₃Y_t +E_t

Q_t^s=Q_t^D (1.6.)

Т.О., в данной модели предопред-ми переменными явл-ся доход и цена, а спрос и предложение яв-ся объясняемыми переменными.

Выбор типа матем-й функции при построении уравнения регрессии Построение модели

Исходные данные: заранее известные (экспериментальные, наблюденные) значения фактора х_i – экзогенная переменная и соответствующие им значения отклика y_i, (i = 1,…,n) - эндогенная переменная;

Активный и пассивный эксперимент.

Выборочные характеристики – позволяют кратко охарактеризовать выборку, т. е., получить ее модель, хотя и очень грубую:

а) среднее арифметическое:

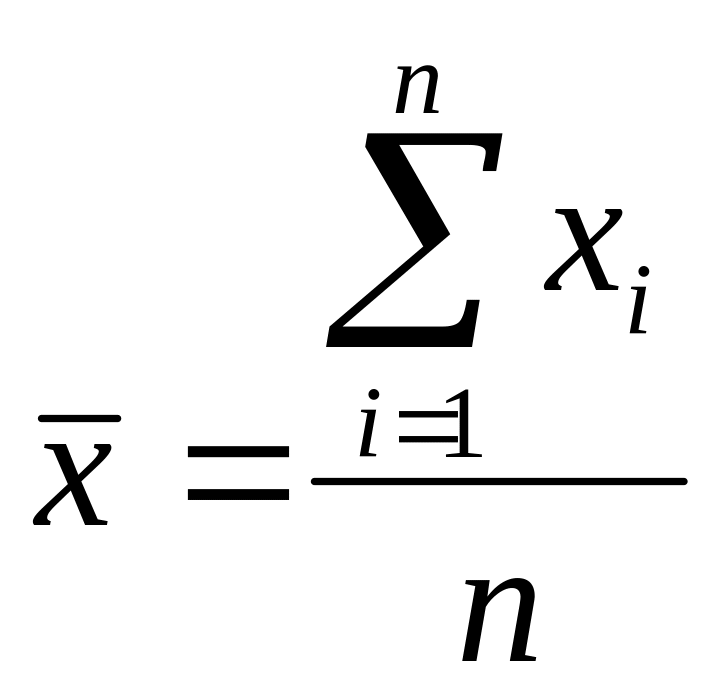
Среднее арифметическое – это «центр», вокруг которого колеблются значения случайной величины.

Основные этапы построения эконометрических моделей

На первом постановочном этапе построения эконометрической модели формируются цели моделирования, определяется набор участвующих в модели факторов, т.е. устанавливается, какие из переменных будут рассматриваться как экзогенные, а какие как эндогенные и лаговые.

Пусть У ={у1 у2 …уm}, множество эндогенных переменных ; Х = {х1 х2 …хm} – множество экзогенных переменных.

Задачей экзогенного моделирования является получение каждой эндогенной переменной от совокупности экзогенных переменных и возможно от части эндогенных.

y1 = f (x1 … xk у2 … уm)

При этом зависимые переменных лаговые.

На 1 ом этапе осуществляется анализ экономической сущности изучаемой модели.

На 3 ем этапе выбор общего вида модели: парная, множественная; сколько должно войти факторов; линейная не линейная; а так же определение коэффициентов функции f.

4 ый этап отбор необходимой статистической информации и предварительный анализ данных.

5 ый этап – идентификация модели, т.е. стат анализ модели, стат оценка независимых параметров модели. Наиболее часто для оценки (нахождения) параметров модели применяют метод наименьших квадратов (МНК)

6 ой этап – сопоставление реальных и модельных значений. Иначе оценка адекватности и точности модели.

Билет 13

1. Гетероскедастичность остатков. Количественная оценка дисперсии ошибок с использованием тестов Уайта и Парка.

2. Спецификация моделей множественной регрессии.

3. МНК для нелинейной регрессии.

4. Понятие коэффициента регрессии. Его значение для линейной и степенной зависимостей.

Билет 14

1.Проблема гетероскедастичности. Тест Глейзера .

Гетероскедастичность остатков модели регрессии

Термин гетероскедастичность в широком смысле понимается как предположение о дисперсии случайных ошибок модели регрессии.

Под гомоскедастичностью понимается предположение о том, что дисперсия случайной ошибки βi является известной постоянной величиной для всех наблюдений.

Но на практике предположение о гомоскедастичности случайной ошибки βi или остатков модели регрессии ei выполняется не всегда.

Под гетероскедастичностью (heteroscedasticity – неоднородный разброс) понимается предположение о том, что дисперсии случайных ошибок являются разными величинами для всех наблюдений, что означает нарушение второго условия нормальной линейной модели множественной регрессии:

Гетероскедастичность остатков модели регрессии может привести к негативным последствиям:

1) оценки неизвестных коэффициентов нормальной линейной модели регрессии являются несмещёнными и состоятельными, но при этом теряется свойство эффективности;

2) существует большая вероятность того, что оценки стандартных ошибок коэффициентов модели регрессии будут рассчитаны неверно, что конечном итоге может привести к утверждению неверной гипотезы о значимости коэффициентов регрессии и значимости модели регрессии в целом.

Тест Глейзера обнаружения гетероскедастичности остатков модели регрессии

Существует несколько тестов на обнаружение гетероскедастичности остатков модели регрессии.

Рассмотрим применение теста Глейзера на примере линейной модели парной регрессии.

Коэффициент Спирмена является аналогом парного коэффициента корреляции, однако, с его помощью можно оценить тесноту зависимости не только между количественными, но и между количественными и качественными переменными.

Коэффициент Спирмена рассчитывается по формуле:

где d – ранговая разность (Rx– Re);

n – количество пар вариантов.

Если тест Глейзера проводился для линейной модели множественной регрессии, то при принятии основной гипотезы делается вывод о том, что гетероскедастичность не зависит от выбранной переменной xmi.

2.Сформулировать основные предпосылки принятия МНКдля построения регрессионной модели.

Различают 5 предпосылок :

-случайный характер остатков

-нулевая средняя величина не зависящая от хi

-гомоскедастичность -дисперсия каждого отклонения одинакова для всех значений х

-отсутствие автокорреляции остатков

-остатки подлежат нормальному закону распределения