
- •1.Уравнение в частных производных
- •2.Основные типы уравнений
- •3.Линейное однородное ду в частных производных первого порядка
- •4.Вывод уравнения колебаний струны методом Фурье
- •5.Задачи Коши
- •6.Решение уравнений колебаний струны методом Фурье
- •7.Решение волнового уравнения методом д′Аламбера
- •8.Уравнение теплопроводности для однородного стержня
- •9.Уравнение теплопроводности в пространстве
- •10.Распростронение тепла в неограниченном стержне. Интервал Пуасснова
- •11.Задачи приводящие к уравнению Лапласа
- •12.Задачи Неймана и Дирихле
- •Внешняя задача Неймана
- •13.Решение задачи Дирихле для уравнения Лапласа в круге методом Фурье
- •14.Случайное событие. Относительная частота случайного события. Вероятность события.
- •15.Теорема я.Бернулли
- •16.Совместные и несовместимые события. Полная группа парами несовместимых событий
- •17.Геометрическая интерпретация событий
- •18.Операции над событиями
- •19.Аксиомотическое определение вероятности
- •20.Теорема о сложении вероятностей. Примеры
- •21.Геометрическая интерпретация вероятностей. Вывод формулы для суммы совместимых событий
- •22.Умножение вероятностей
- •23.Условная вероятность
- •Определение
- •Замечания
- •24.Полная вероятность. Формула Байеса
- •25.Дискретные случайные величины и их характеристики
- •26.Относительная частота и вероятность для дискретных случайных величин
- •27.Математическое ожидание дискретной случайной величины
- •28.Дисперсия, средневековое отклонение, моменты дискретной случайной величины
- •Определение
- •Замечания
- •Свойства
- •29.Непрерывные случайные величины. Функция распределения и плотности вероятности
- •30.Теорема о связи функции распределения с плотностью вроятности
- •31.Интегральный закон распределения. Интегральная кривая
- •32.Числовые характеристики непрерывных случайных величин
- •33.Медиана и мода
- •34.Нормальный закон распределения
- •35.Медиана и мода нормального закона распределения
- •36.Интеграл вероятностей
- •37.Свойства интеграла вероятностей
- •38.Функция Лапласа
- •39.Среднее отклонение и средняя ошибка
- •40.Приведенная функция Лапласа
- •41.Правило трех сигм
- •42.Закон больших чисел. Предельные теоремы
- •43.Задачи математической статистики. Выборка, эмпирическая функция распределения
- •44.Статистический ряд и гистограмма
- •45.Среднее взвешенное и статистическая дисперсия
- •46.Точечные оценки
- •47.Распределение Пуасона
- •48.Распределение Стьюдента
- •49.Основные свойства точечной оценки
- •50.Исправленная выборочная дисперсия
- •51.Стандартная ошибка среднего арифметического
- •52.Интервальные оценки параметров распределения
- •53.Доверительный интервал, границы
- •54.Проверка статистических гипотез
- •55.Корреляционный анализ
- •56.Регрессионный анализ
28.Дисперсия, средневековое отклонение, моменты дискретной случайной величины
Диспе́рсия
случа́йной величины́ —
мера разброса данной случайной
величины,
то есть её отклонения от математического
ожидания.
Обозначается ![]() в
русской литературе и
в
русской литературе и ![]() (англ. variance)
в зарубежной. В статистике часто
употребляется обозначение
(англ. variance)
в зарубежной. В статистике часто
употребляется обозначение ![]() или
или ![]() .
Квадратный корень из дисперсии, равный
.
Квадратный корень из дисперсии, равный ![]() ,
называется среднеквадрати́чным
отклоне́нием, станда́ртным
отклоне́нием или
стандартным разбросом. Стандартное
отклонение измеряется в тех же единицах,
что и сама случайная величина, а дисперсия
измеряется в квадратах этой единицы
измерения.
,
называется среднеквадрати́чным
отклоне́нием, станда́ртным
отклоне́нием или
стандартным разбросом. Стандартное
отклонение измеряется в тех же единицах,
что и сама случайная величина, а дисперсия
измеряется в квадратах этой единицы
измерения.
Из неравенства Чебышева следует, что случайная величина удаляется от её математического ожидания на более чем k стандартных отклонений с вероятностью менее 1/k². Так, например, как минимум в 75 % случаев случайная величина удалена от её среднего не более чем на два стандартных отклонения, а в примерно 89 % — не более чем на три.
Определение
Пусть ![]() —
случайная величина, определённая на
некотором вероятностном
пространстве.
Тогда
—
случайная величина, определённая на
некотором вероятностном
пространстве.
Тогда
![]()
где
символ ![]() обозначает математическое
ожидание[1][2].
обозначает математическое
ожидание[1][2].
Замечания
Если случайная величина вещественна, то, в силу линейности математического ожидания, справедлива формула:
![]()
Дисперсия является вторым центральным моментом случайной величины;
Дисперсия может быть бесконечной. См., например, распределение Коши.
Дисперсия может быть вычислена с помощью производящей функции моментов
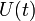 :
:
![]()
Дисперсия целочисленной случайной величины может быть вычислена с помощью производящей функции последовательности
Свойства
Дисперсия любой случайной величины неотрицательна:
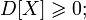
Если дисперсия случайной величины конечна, то конечно и её математическое ожидание;
Если случайная величина равна константе, то её дисперсия равна нулю:
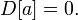 Верно
и обратное: если
Верно
и обратное: если 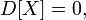 то
то 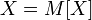 почти
всюду;
почти
всюду;Дисперсия суммы двух случайных величин равна:
![]() ,
где
,
где ![]() —
их ковариация;
—
их ковариация;
Для дисперсии произвольной линейной комбинации нескольких случайных величин имеет место равенство:
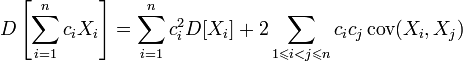 ,
где
,
где ![]() ;
;
В частности,
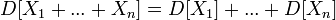 для
любых независимых или некоррелированных случайных
величин, так как их ковариации равны
нулю;
для
любых независимых или некоррелированных случайных
величин, так как их ковариации равны
нулю;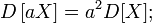
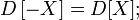
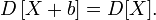
Пример
Пусть
случайная величина ![]() имеет
стандартное непрерывное
равномерное распределение на
имеет
стандартное непрерывное
равномерное распределение на ![]() то
есть её плотность
вероятности задана
равенством
то
есть её плотность
вероятности задана
равенством
![]()
Тогда математическое ожидание квадрата случайной величины
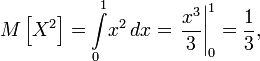
и математическое ожидание случайной величины
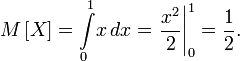
Тогда дисперсия случайной величины
![]()
29.Непрерывные случайные величины. Функция распределения и плотности вероятности
Функцией распределения вероятностей называют функцию F(x), определяющую вероятность того, что случайная величина X в результате испытания примет значение, меньшее x, то есть:
![]()
Случайную величину называют непрерывной, если ее функция распределения вероятностей есть непрерывная, кусочно-дифференцируемая функция с непрерывной производной.
Свойства функции распределения вероятностей случайной величины
1.
Значения функции распределения
вероятностей принадлежат отрезку
![]() :
:
![]()
2. Функция распределения вероятностей – неубывающая функция, то есть:
![]() ,
если
,
если
![]() .
.
Следствие.
Если![]() возможные значения непрерывной случайной
величины расположены на всей числовой
оси, то справедливы следующие предельные
соотношения:
возможные значения непрерывной случайной
величины расположены на всей числовой
оси, то справедливы следующие предельные
соотношения:
![]() ;
;
![]() .
.
Плотностью
распределения
вероятностей непрерывной случайной
величины X
называют функцию f(x)
– первую производную от функции
распределения вероятностей F(x):
![]()
Таким образом, функция распределения вероятностей является первообразной для плотности распределения вероятностей.
Свойства плотности распределения вероятностей
1. Плотность распределения вероятностей – неотрицательная функция:
2. Несобственный интеграл от плотности распределения вероятностей в пределах от -∞ до +∞ равен единице:
