
- •35. Исследование функции на интервале монотонности. Экстремум ф-ии необходимое и достаточное условие экстремума.
- •37. Асимптоты. Вертикальные, горизонтальные, наклонные. Их нахождение.
- •38. Наибольшее и наименьшее значения ф-ии непрерывной на отрезке. Общий план исследования ф-ий и построения их графиков.
- •39. Функции нескольких переменных (фнп). Определения. Ооф. Геометрич смысл.
- •40. Линии уровня, градиент для ф-ии 2-х переменных.
- •41. Частное и полное приращение ф-ии. Предел ф-ии 2-х переменных. Непрерывность фнп.
- •42. Частные производные фнп.
- •43. Дифференциалы фнп.
- •44. Дифференцирование сложной ф-ии нескольких переменных.
- •45. Производных высших порядков для 2-х переменных.
- •46. Экстремум ф-ии 2-х переменных. Необходимое условие существ-я экстремума.
- •47. Достаточное усл-е существ-я экстремума для ф-ии 2-х переменных.
- •48. Первообразная и неопределенный интеграл.
- •49. Свойства неопределенного интеграла.
- •50. Таблица неопределенных интегралов.
- •51. Методы интегрирования. Непосредственное интегрирование. Метод подставки. Интегрирование по частям.
- •52. Интегрирование простейших дробей.
- •53. Разложение рациональных дробей на простейшие. Интегрирование рациональных дробей. Метод неопределенных коэффициентов.
- •54. Интегрирование простейших иррациональных выражений.
- •55. Интегрирование тригонометрических функций. Универсальная тригонометрическая подстановка.
- •56. Интегральные суммы. Понятие определенного интеграла.
- •57. Связь неопределенного интеграла с определенным. Формула Ньютона-Лейбница.
- •58. Свойства определенного интеграла.
- •59. Вычисление определенного интеграла по частям.
- •60. Замена переменной в определенном интеграле.
- •61. Несобственные интегралы с ∞-ми пределами.
- •62. Несобственные интегралы от разрывных функций.
57. Связь неопределенного интеграла с определенным. Формула Ньютона-Лейбница.
Q(x), y=f(x) [a,b], x€[a,b]. Q(b)=Q, Q(a)=0, дельта Q(x)=Q(x+дельта x)-Q(x). Если в (.)x f(x) возраст => f(x)дельта х<дельтаQ(x)<f(x+дельта х)дельта х. f(x) < дельтаQ(x)/дельта х<f(x+дельта х). f(x)≤ limдельта х→0 дельтаQ(x)/дельта х≤ limдельта х→0 f(x+дельта х)=f(x). Q`(x)=f(x). Q(x) – первообразн для f(x), одна из первообразных. Q(x)=F(x)+C1. Q(a)=F(a)+C1=0 => C1=-F(a).
Q(x)= ⌡xaf(x)dx=F(x)- F(a).
⌡baf(x)dx= F(b)- F(a), F`(x)=f(x). – ф-ла Ньютона-Лейбница
58. Свойства определенного интеграла.
1. Интегр с одинак границами=0
⌡aaf(x)dx=0
2. От перестановки Лима интегр меняет знак
⌡abf(x)dx=-⌡baf(x)dx
3. Опред интегр не завис от обозн-я перемен интегр-я.
⌡abf(x)dx=⌡abf(t)dt
4. Посторон множитель можно вносить и выносить под знак опред интегр
⌡ab K f(x)dx=K⌡ab f(x)dx, K=const
5. Определ интеграл от алгебраич суммы конечного числа ф-ии=алгебраич сумме интегралов от тех же ф-ий.
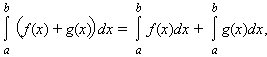
6. Для любого С
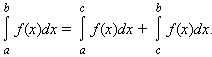
7. Если одна ф-ия больше другой, a<b => интеграл первой больше второго
Cл-е
1:
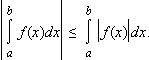
8. М-наиб, m-наим f(x)[a,b], a<b, то m*(b-a)≤ ⌡abf(x)dx ≤M*(b-a).
m≤f(x) ≤M для всех(любой) x€[a,b]; ⌡ab m dx≤ ⌡abf(x)dx ≤⌡ab M dx => m*(b-a)≤ ⌡abf(x)dx ≤M*(b-a) чтд.
9. Теор о среднем.
Если f(x) непрерывн на [a,b], то сущ(.) ξ € [a,b], такая, что ⌡abf(x)dx=(b-a)f(ξ), ξ€ [a,b].
f(ξ)=1/(b-a)*⌡abf(x)dx – опред средн знач ф-ии f(x) на интервале [a,b].
10. Опред интеграл с перемен верх лимом и непр подынтегр ф-ией=сам есть непр-ная ф-ия своего верх Лима.
⌡axf(x)dx=F(x)-F(a)=f(x)
11. Производно пред интеграла по перемен верх предел=подыинтегральн ф-ии знач верх предел, если она непрерывна.
[⌡axf(x)dx]`x=f(x) => разлож на [F(x)]`=f(x) и [F(a)]`=0
59. Вычисление определенного интеграла по частям.
⌡UdV=UV-⌡VdU
⌡abUdV=[⌡UdV]|ba=[UV-⌡VdU]|ba= UV|ba – [⌡VdU]|ba= UV|ba - ⌡abVdU
⌡abUdV= UV|ba - ⌡abVdU – форм интегр по част для опред интеграла
60. Замена переменной в определенном интеграле.
Теор: ⌡abf(x)dx. Введ новой переменной x=φ(t) => dx= φ`(t)dt
Если: 1) φ(λ)=а, φ(β)=b. 2) φ(t) и φ`(t) непрерывна [λ, β]. 3) f[φ(t)] определена и непр [λ, β].
⌡abf(x)dx=⌡λ βf[φ(t)]* φ`(t)dt.
X|| a| b
T|| λ| β
61. Несобственные интегралы с ∞-ми пределами.
Определенный
интеграл![]() где
промежуток интегрирования [а; b] конечный,
а подынтегральная функция ƒ(х) непрерывна
на отрезке [а; b], называют еще собственным
интегралом.
где
промежуток интегрирования [а; b] конечный,
а подынтегральная функция ƒ(х) непрерывна
на отрезке [а; b], называют еще собственным
интегралом.
Рассмотрим так называемые несобственные интегралы, т. е. определенный интеграл от непрерывной функции, но с бесконечным промежутком интегрирования или определенный интеграл с конечным промежутком интегрирования, но от функции, имеющей на нем бесконечный разрыв.
40.1. Интеграл с бесконечным промежутком интегрирования (несобственный интеграл I рода)
Пусть
функция ƒ(х) непрерывна на промежутке
[а;+∞). Если существует конечный предел![]() то
его называютнесобственным
интегралом первого родаи
обозначают
то
его называютнесобственным
интегралом первого родаи
обозначают![]()
Таким образом, по определению
![]() ⌡+∞a
f(x)dx=limb=>+∞[F(b)-F(a)]=F(∞)-F(a)
⌡+∞a
f(x)dx=limb=>+∞[F(b)-F(a)]=F(∞)-F(a)
В этом
случае говорят, что несобственный
интеграл![]() сходится.
сходится.
Если
же указанный предел не существует или
он бесконечен,то говорят, что
интеграл ![]() dx расходится.
dx расходится.
Аналогичноопределяется
несобственный и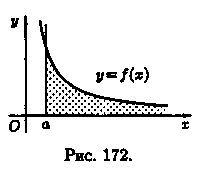 нтеграл
на промежутке (-∞; b]:
нтеграл
на промежутке (-∞; b]:
![]()
Несобственный интеграл с двумя бесконечны ми пределами определяется формулой
![]() где
с — произвольное число.
где
с — произвольное число.
В этом
случае интеграл слева сходится лишь
тогда, когда сходятся оба интеграла
справа. Отметим, что если непрерывная
функция ƒ (х) ≥ 0 на промежутке [а; +∞) и
интеграл![]() сходится,
то он выражает площадь бесконечно
длинной криволинейной трапеции (см.
рис. 172).
сходится,
то он выражает площадь бесконечно
длинной криволинейной трапеции (см.
рис. 172).
Пример 40.1. Вычислить несобственные интегралы или установить их расходимость:
1) ![]() 2)
2)![]() 3)
3)![]()
Решение:
1)![]() интеграл
сходится;
интеграл
сходится;
2)![]() интеграл
расходится, так как при а →-∞ предел
интеграл
расходится, так как при а →-∞ предел![]() не
существует.
не
существует.
3)![]() интеграл
расходится.
интеграл
расходится.
В некоторых задачах нет необходимости вычислять интеграл; достаточно лишь знать, сходится ли он или нет.
Приведем без доказательства некоторые признаки сходимости.
Теорема 40.1 (признак сравнения). Если на промежутке [а; +∞) непрерывные функции ƒ(х) и φ(х) удовлетворяют условию 0 ≤ ƒ(х) ≤φ(х), то из сходимости
интеграла![]() следует
сходимость интеграла
следует
сходимость интеграла![]() а
из расходимо-
а
из расходимо-
сти
интеграла ![]() следует
расходимость интеграла
следует
расходимость интеграла![]()
Пример
40.2. Сходится ли интеграл![]()
Решение:
При х ≥ 1 имеем![]() Но
интеграл
Но
интеграл![]() сходится.
Следовательно, интеграл
сходится.
Следовательно, интеграл![]() также
сходится (и его значение меньше 1).
также
сходится (и его значение меньше 1).
Теорема
40.2. Если существует предел![]() и φ(х)
> 0), то интегралы
и φ(х)
> 0), то интегралы![]() одновременно
оба сходятся или оба расходятся (т. е.
ведут себя одинаково в смысле сходимости).
одновременно
оба сходятся или оба расходятся (т. е.
ведут себя одинаково в смысле сходимости).
Пример
40.3. Исследовать сходимость интеграла![]()
Решение:
Интеграл![]() сходится,
так как интеграл
сходится,
так как интеграл ![]() сходится
и
сходится
и
![]()
Теор2: Пусть f(x) знако перемен ф-ия. 1) ⌡+∞a f(x)dx=1, 2) ⌡+∞a |f(x)|dx=2.=>1) Если 2 сход, то 1 сход – абсолют, 2) 2 расход – про 1 ничего сказать нельзя.
