11) Схема испытаний Бернулли. Число возможных исходов при n испытаниях Бернулли. Вероятность k успехов при n испытаниях Бернулли

Опр: Повторенные испытания Бернулли, называются испытания из двух вариантов: успешные с вероятностью «p», и неуспешные с вероятностью «q=q-p»

n испытаний Бернулли

УННУ…ННН= n букв

возможных исходов

(k) – вероятность k успехов при n испытаниях.

УУУННН, где УУУ приянадлежит k, а УУУННН принадлежит n

=

(k)= - биномиальное распределение

Под схемой Бернулли понимают конечную серию повторных независимых испытаний с двумя исходами. Вероятность появления (удачи) одного исхода при одном испытании обозначают p=P(Y), а непоявления (неудачи) его P(H)=q=1-p . Я. Бернулли установил, что вероятность ровно k успехов в серии из n повторных независимых испытаний вычисляется по следующей формуле:

(k)=

То значение , при котором число (k)является максимальным из множества { (k)}, называется наивероятнейшим.

12) Локальная теорема Муавра-Лапласа

ЛАПЛАСА ТЕОРЕМА - одна из предельных теорем теории вероятностей. Если при каждом из n независимых испытаний вероятность появления некоторого случайного события Е равна р (0"р"1) и m - число испытаний, в которых Е фактически наступает, то вероятность неравенства близка (при больших n) к значению интеграла Лапласа. Установлена П. Лапласом (1812).

Локальная теорема Муавра — Лапласа. Если в схеме Бернулли число n велико, а число p отлично от 0 и 1, тогда:

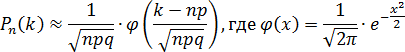
Функция φ(x) называется функцией Гаусса. Ее значения давно вычислены и занесены в таблицу, которой можно пользоваться даже на контрольных работах и экзаменах.

Функция Гаусса обладает двумя свойствами, которые следует учитывать при работе с таблицей значений:

1. φ(−x) = φ(x) — функция Гаусса — четная;

2.При больших значениях x имеем: φ(x) ≈ 0.

Локальная теорема Муавра — Лапласа дает отличное приближение формулы Бернулли, если число испытаний n достаточно велико. Разумеется, формулировка «число испытаний достаточно велико» весьма условна, и в разных источниках называются разные цифры. Например:

1.Часто встречается требование: n · p · q > 10. Пожалуй, это минимальная граница;

2.Другие предлагают работать по этой формуле только для n > 100 и n · p · q > 20.

Локальная теорема Лапласа.

Если n – велико, а р – отлично от 0 и 1, то

где - функция Гаусса (функция табулирована)

13) Интегральная теорема Муавра-Лапласа

Если n – велико, а р – отлично от 0 и 1, то

P(n; k1, k2) где - функция Лапласа (функция табулирована)

Функции Гаусса и Лапласа обладают свойствами, которые необходимо знать при использовании таблиц значений этих функций:

а)

б) при больших верно.

Теоремы Лапласа дают удовлетворительное приближение при . Причем чем ближе значения к 0,5, тем точнее данные формулы. При маленьких или больших значениях вероятности (близких к 0 или 1) формула дает большую погрешность (по сравнению с исходной формулой Бернулли).

Пример. Для мастера определенной квалификации вероятность изготовить деталь отличного качества равна 0,75. За смену он изготовил 400 деталей. Найти вероятность того, что в их числе 280 деталей отличного качества.

Решение. По условию , откуда

По таблицам найдем .

Искомая вероятность равна: