51.Постулаты Боpа.

Первый постулат Бора (постулат стационарных состояний):

существуют определенные дискретные стационарные состояния атома, находясь в которых, он не излучает энергию. Каждое стационарное состояние характеризуется определенным значением энергии. Из одного состояния в другое атом может переходить путем квантового перехода.

Правило квантования орбит Бора утверждает, что в стационарном состоянии атома электрон, двигаясь по орбите, должен иметь квантованные значения момента импульса, удовлетворяющие для круговых орбит условию , где – масса электрона; – его скорость на п-й орбите радиусом .

Второй постулат Бора (правило частот):

излучение происходит только при переходе атома из одного стационарного состояния с большей энергией 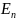в другое стационарное состояние с меньшей энергией . Такой переход сопровождается испусканием электромагнитного излучения с энергией

, равной разности энергий соответствующих стационарных состояний. Возможен и обратный процесс, в котором атом переходит из одного стационарного состояния в другое, более высокое. При этом атом поглощает фотон с энергией, равной разности энергий этих стационарных состояний. Набор всевозможных дискретных частот квантовых переходов ω, определяемых из правила, описывает линейчатый спектр атома.

52.Атом водорода.

Согласно Рез-ду, атом водорода представляет собой ядро с атомным весом 1 и с зарядом +е (протон), около которого обращается один электрон, удерживаемый вблизи ядра кулоновской силой электростатического притяжения. Пользуясь законами механики, нетрудно вычислить, что электрон должен описывать эллиптическую орбиту, в фокусе которой находится протон. Энергия такой системы

где а - большая полуось эллипса; частота обращения электрона по орбите определиться из соотношения

где - масса электрона.

Так как энергия данной системы не зависит от эксцентриситета эллипса, то те же формулы справедливы и для круговой орбиты диаметра 2а.

53.Спектpы водоpодоподобных атомов.

Спектр водородного атома по Бальмеру-Ридбергу описывается формулой:

58.Опыт Штерна и Герлаха.

О. Штерном и В. Герлахом были по­ставлены опыты целью которых являлось измерение магнитных моментов атомов различных химических элементов. Для определения моментов и одного электрона опыты должны быть поставлены с атомами, у которых орбитальные механические (и магнитные) моменты всех электронов, кроме одного, взаимно компенсируют друг друга. Такими атомами являются атомы химических элементов, образующие первую группу периодической системы Менделеева и имеющие один валентный электрон на внешней оболочке.

Идея опытов Штерна и Герлаха заключалась в измерении силы, действующей на атом в неоднородном магнитном поле. В таком магнитном поле на атом должна дей­ствовать сила . Здесь – проекция магнитного момента атома на направление z магнитного поля, а В — индукция магнитного поля (на­правленная вдоль оси Z), неоднородного только вдоль этой же оси.Опыты Штерна и Герлаха обнаружили ошибочность классического предположения о том, что магнитный момент и механиче­ский момент импульса атома произвольно ориентируются относительно направления внешнего поля, и подтвердили наличие про­странственного квантования. И если бы момент импульса L; атома (и его магнитный момент р_т) мог принимать произвольные ориентации в магнитном поле, то можно было бы ожидать непрерывного распределения попаданий атомов на пластинку с большей плотностью попаданий в середине пластинки и меньшей плотностью к ее краям. Опыты, проведенные с серебром и атомами других элементов периодической системы, привели к совершенно другому результату.