45.Стационаpные состояния.

Стационарными состояниями называют состояния, в которых все наблюдаемые физические величины не изменяются с течением времени. В стационарных состояниях состояние частицы в данный момент времени описывается периодической функцией времени с циклической частотой . При этом -функция определяется полной энергией частицы: , где функция не зависит от времени, а выражение для частоты следует из соотношения, связывающего полную энергию Е частицы (в случае стационарного поля E = const) и частоту де-бройлевской волны.

47.Туннельный эффект.

Туннельный эффект (туннели́рование) — преодоление микрочастицей потенциального барьера в случае, когда её полная энергия (остающаяся при туннелировании неизменной) меньше высоты барьера. Туннельный эффект — явление исключительно квантовой природы, невозможное в классической механике. Аналогом туннельного эффекта в волновой оптике может служить проникновение световой волны внутрь отражающей среды (на расстояния порядка длины световой волны) в условиях, когда, с точки зрения геометрической оптики, происходит полное внутреннее отражение. Явление туннелирования лежит в основе многих важных процессов в атомной и молекулярной физике, в физике атомного ядра, твёрдого тела и т. д.

49 Квантование энергии и импульса частицы.

Квантование энергии:

Учтем, что физический смысл имеют лишь такие решения уравнения, когда не временная волновая функция и ее первые производные по координатам удовлетворяют стандартным условиям. Эти условия являются требованиями, накладываемыми на искомое решение дифференциального уравнения. Решения уравнения Шрёдингера, удовлетворяющие этим условиям, оказываются возможными лишь при некоторых значениях энергии Е, называемых собственными значениями энергии. Функции , являющиеся решениями уравнения при этих значениях энергии, называются собственными функциями, принадлежащими собственным значениям Е.

Собственные значения Е могут образовывать как непрерывный, так и дискретный ряд. В первом случае говорят о непрерывном (сплошном) спектре энергии, во втором – о ее дискретном спектре.

Уравнение Шрёдингера является математическим выражением корпускулярно-волнового дуализма. Оно удовлетворяет принципу соответствия Бора и в предельном случае, когда длина волны де Бройля значительно меньше размеров, характерных для рассматриваемого движения, позволяет описать движение частиц по законам классической механики.

Для описания состояния квантовой системы в данный момент времени вводится комплексная волновая функция (пси-функция)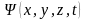 . Она определяется так, что вероятность dP нахождения частицы в некоторый момент времени в элементе объема dV прямо пропорциональна и элементу объема dV : где ; – функция, комплексно сопряженная c . Волновую функцию называют амплитудой вероятности. Пси-функция непосредственно не измеряется на опыте.