38.Масса фотона.

Фотон - мельчайшая частица электромагнитного излучения, имеющая энергию в один квант.

по теории Планка:

по теории Энштейна:

отсюда следует

Фотон не имеет массы покоя ( m0 = 0), так как он не может существовать в состоянии покоя. Все фотоны движутся со скоростью с = 3·108 м/с.

40.Гипотеза де Бройля.

Гипотеза де Бройля заключается в том, что французский физик Луи де Бройль выдвинул идею приписать волновые свойства электрону. Проводя аналогию между квантом, де Бройль предположил, что движение электрона или какой-либо другой частицы, обладающей массой покоя, связано с волновым процессом.

Гипотеза де Бройля устанавливает, что движущейся частице, обладающей энергией E и импульсом p, соответствует волновой процесс, частота которого равна:

а длина волны:

где p - импульс движущейся частицы.

39.Энергия и импульс фотона.

Порция светового излучения - квант света - обладает корпускулярными свойствами и может рассматриваться как элементарная частица, называемая фотоном. Фотоны являются носителями свойств электромагнитного поля. Чем выше частота излучения, тем сильнее проявляются корпускулярные (или квантовые) свойства света.

Световые частицы - фотоны - обладают энергией

, где h - постоянная Планка; лямбда - длина световой волны; v - ее частота; с - скорость света.

Согласно соотношению Эйнштейна между массой и энергией, следующему из теории относительности

Масса фотона, определяемая из этих формул, - это масса движущегося фотона, так как в состоянии покоя фотон не существует. Скорость, с которой движется фотон, равна скорости света.

Найдем импульс фотона:

То, что фотон обладает импульсом, экспериментально подтверждается открытием светового давления.

Если свет является монохроматическим, то все фотоны в этом случае имеют одинаковые энергию, массу и импульс.

Фотоны возникают (излучаются) при переходах атомов, молекул, ионов и атомных ядер из возбужденных энергетических состояний в состояния с меньшей энергией.

Фотоны излучаются также при ускорении и торможении заряженных частиц, при распадах некоторых частиц и уничтожении пары электрон-позитрон.

Процесс поглощения света веществом сводится к тому, что фотоны целиком передают свою энергию частицам вещества. Процесс поглощения света рассматривается в квантовой физике как дискретный и во времени, и в пространстве.

42 Соотношение неопpеделенностей.

Квантовая механика утверждает, что положение и скорость микробъекта одновременно не могут быть точно известны. Эта идея составляет суть принципа неопределенности, открытого В. Гейзенбергом. Количественные соотношения, выражающие этот принцип в конкретных случаях, называют соотношениями неопределенностей. Если - неопределенность значения координаты х центра масс системы, а – неопределенность проекции импульса 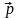на ось Х, то произведение этих неопределенностей должно быть не меньше постоянной Планка .

_{Соотношение неопределенностей, устанавливающее неопределенность измерения энергии} за данный промежуток времени , имеет вид