6 Вопрос

Равноускоренное движение — движение, при котором ненулевой вектор ускорения остаётся неизменным по модулю и направлению.

Примером такого движения является движение тела, брошенного под углом   к горизонту в однородном поле силы тяжести — тело движется с постоянным ускорением  , направленным вертикально вниз.

При равноускоренном движении по прямой скорость тела определяется формулой:

Зная, что  , найдём формулу для определения координаты x:

Примечание. Равнозамедленным можно назвать движение, при котором модуль скорости равномерно уменьшается со временем (если вектора   и   противонаправлены). Равнозамедленное движение также является равноускоренным.

Перемещение в случае одномерного равноускоренного движения

В случае одномерного равноускоренного движения вдоль координаты x имеет место формула:

,

Скорость

Для характеристики движения материальной точки вводится векторная величина — скорость, которой определяется как быстрота движения, так и его направление в данный момент времени.

Пусть материальная точка движется по какой-либо криволинейной траектории так, что в момент времени t ей соответствует радиус-вектор г₀ (рис. 3). В течение малого промежутка времени Dt точка пройдет путь Ds и получит элементарное (бесконечно малое) перемещение Dг.

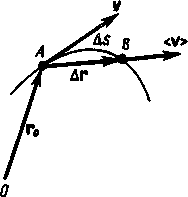
Рис. 3

Вектором средней скорости <v> называется отношение приращения Dг радиуса-вектора точки к промежутку времени Dt:

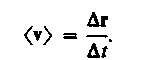
(2.1)

Направление вектора средней скорости совпадает с направлением Dг. При неограниченном уменьшении Dt средняя скорость стремится к предельному значению, которое называется мгновенной скоростью v:

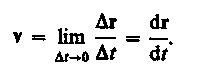
Мгновенная скорость v, таким образом, есть векторная величина, равная первой производной радиуса-вектора движущейся точки по времени. Так как секущая совпадает с касательной, то вектор скорости v направлен по касательной к траектории в сторону движения (рис. 3). По мере уменьшения Dt путь Ds все больше будет приближаться к |Dг|, поэтому модуль мгновенной скорости

Таким образом, модуль мгновенной скорости равен первой производной пути по времени:

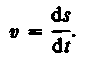(2.2)

При неравномерном движении модуль мгновенной скорости с течением времени изменяется. В данном случае пользуются скалярной величиной <v> — средней скоростью неравномерного движения:

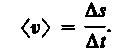
Из рис. 3 вытекает, что <v> > |<r>|, так как Ds >|Dг|, и только в случае прямолинейного движения

Если выражение ds=vdt (см. формулу (2.2)) проинтегрировать по времени в пределах от t до t+Dt, то найдем длину пути, пройденного точкой за время Dt:

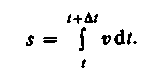
(2.3)

В случае равномерного движения числовое значение мгновенной скорости постоянно; тогда выражение (2.3) примет вид

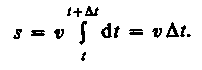
Длина пути, пройденного точкой за промежуток времени от t\ до fa, дается интегралом

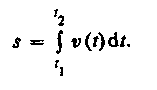
Ускорение и его составляющие

Ускорение – характеризует быстроту изменения скорости по величине и направлению.

- полное ускорение = геометрической сумме (векторной) нормального и тангенсуального ускорения. =а +а

Рассмотрим плоское движение, т. е. движение, при котором все участки траектории точки лежат в одной плоскости. Пусть вектор v задает скорость точки А в момент времени t. За время Dt движущаяся точка перешла в положение В и приобрела скорость, отличную от v как по модулю, так и направлению и равную v₁ = v + Dv. Перенесем вектор v₁ в точку А и найдем Dv (рис. 4).

Рис. 4

Средним ускорением неравномерного движения в интервале от t до t+Dr называется векторная величина, равная отношению изменения скорости Ду к интервалу времени Dг:

Мгиовеивым ускорением а (ускорением) материальной точки в момент време ни t будет предел среднего ускорения:

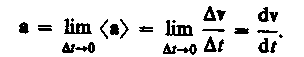
Таким образом, ускорение а есть векторная величина, равная первой производной скорости по времени.

Разложим вектор Dv на две составляющие. Для этого из точки А (рис. 4) по направлению скорости v отложим вектор 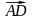, по модулю равный v₁. Очевидно, что вектор 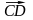, равный Dvt, определяет изменение скорости за время Dt по модулю: Dvt = v₁ - v. Вторая же составляющая Dv_n вектора Dv характеризует изменение скорости за время Dt по направлению.

Тангенциальная составляющая ускорения – составляющая полного ускорения тела криволинейного движения материальной точки, которая характеризует численное изменение скорости и направленно по касательной в сторону отправления движения.

- нормальное и тангенсуальное ускорение взаимоперпендикулярны.

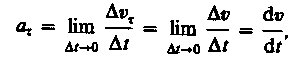
т. е. равна первой производной по времени от модуля скорости, определяя тем самым быстроту изменения скорости по модулю.

Найдем вторую составляющую ускорения. Допустим, что точка В достаточно близка к точке А, поэтому Ds можно считать дугой окружности некоторого радиуса г, мало отличающейся от хорды АВ. Тогда из подобия треугольников АОВ и EAD следует 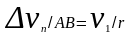, но так как AB=vDt, то

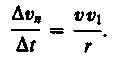
В пределе при Dt ® 0 получим v₁ ® v.

Поскольку v₁ = v, угол EAD стремится к нулю, а так как треугольник EAD равнобедренный, то угол ADE между v и Dv_n стремится к прямому. Следовательно, при Dt ® 0 векторы Dv_n и v оказываются взаимно перпендикулярными. Так как вектор скорости направлен по касательной к траектории, то вектор Dv_n, перпендикулярный вектору скорости, направлен к центру ее кривизны. Вторая составляющая ускорения, равная

называется нормальной составляющей ускорения (составляющая полного ускорения тела (центростремительного) криволинейного движения материальной точки, которая характеризует быстроту изменения скорости по направлению и направлена по главной нормали траектории движения в сторону центра кривизны) поэтому ее называют также центростремительным ускорением). Полное ускорение тела есть геометрическая сумма тангенциальной и нормальной составляющих (рис. 5):

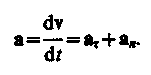
Формула пути при равномерном движении.. Скоростью равномерного прямолинейного движения называют векторную величину, равную отношению перемещения тела к промежутку времени, в течение которого было совершено это перемещение:  v=s/t.

Формула перемещения при равноускоренном движении используется при доказательстве теоремы о кинетической энергии. Для этого необходимо перенести ускорение в левую часть и домножить обе части на массу тела:

.

Записав аналогичные соотношения для координат y и z и просуммировав все три равенства получим соотношение:

.

Слева стоит работа постоянной равнодействующей силы  , а справа — разность кинетических энергий в конечный и начальный момент движения.