3. Основные законы движения жидкости.

Гидравлические сопротивления

Основными законами, позволяющими решать простейшие задачи о движении жидкостей, являются уравнение Бернулли и уравнение расхода.

Уравнение расхода – условие неразрывности потока несжимаемой жидкости – записывается в виде равенства объемных расходов в любых сечениях трубопровода:

Q = = сonst

Отсюда следует, что средние скорости неразрывного потока обратно пропорциональны площадям этих сечений.

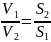
В некоторых задачах о движении жидкости в приближении рассматривается идеальная (невязкая) жидкость.

Уравнение Бернулли для потока идеальной жидкости представляет закон сохранения энергии жидкости вдоль потока: вдоль элементарной струйки идеальной жидкости сумма потенциальной и кинетической энергии является постоянной величиной, т.е.

,

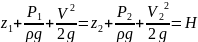где Н - полный гидродинамический напор (полная удельная энергия жидкости в сечении); Z – вертикальная координата центров тяжести сечений (геометрический напор); – пьезометрический напор (удельная энергия давления); U/2g – скоростной напор (удельная кинетическая энергия), сумма представляет собой потенциальную энергию.

В реальных жидкостях проявляется влияние сил внутреннего трения, обусловленных вязкостью, на преодоление которых расходуется определенное количество кинетической энергии или скоростного напора h.

Уравнение Бернулли для потока реальной жидкости записывается в следующем виде

где υ - средняя по сечению скорость; α – коэффициент Кориолиса, учитывающий неравномерность распределения скоростей по сечениям (α=1 только при равномерном распределении скоростей (турбулентный режим движения жидкости)).

Член h выражает потери напора на преодоление различных сопротивлений на пути движения жидкости:

1. Сопротивления по всей длине потока жидкости, вызванные силами трения частиц жидкости между соседними слоями жидкости и трением о стенки, ограничивающие поток.

Потери напора, вызванные этим видом сопротивлений, называют линейными - .

2. Сопротивления, обусловленные местными препятствиями, встречающимися на пути движения (изменение формы и размеров русла). Они ведут к изменению величины и направления скорости.

Потери напора, вызванные этим видом сопротивлений, называют местными - .

Линейные потери напора определяют с помощью формулы Дарси:

,

где l – длина рассматриваемого участка трубопровода; d – диаметр трубопровода; λ – безразмерный коэффициент гидравлического трения.

λ зависит от режима движения жидкости, и определяется числом Рейнольдса, который для трубопровода с круглым сечением вычисляется по формуле:

Для потока произвольной формы число Рейнольдса выражается через гидравлический радиус

Смена режимов происходит при критическом значении числа Рейнольдса, которое составляет . Если число Рейнольдса больше критического значения, то режим движения турбулентный, если меньше – то ламинарный. Критическое значение числа Рейнольдса соответствует нижней критической скорости.

При ламинарном режиме ;

при турбулентном λ зависит от числа Рейнольдса и относительной шероховатости трубы ε :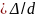

Местные потери напора определяются по формуле Вейсбаха:

где υ – средняя скорость потока в сечении перед местным сопротивлением ζ – коэффициент местного сопротивления (определяется формой местного сопротивления и его геометрическими параметрами).

При внезапном расширении трубы потеря напора происходит при вводе жидкости в силовые цилиндры, пневмогидравлические аккумуляторы, фильтры и прочие устройства. Величина этой потери равна скоростному напору потерянной скорости (теорема Борда):

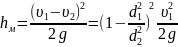
Обозначим - коэффициент местных сопротивлений при расширении трубы, где d₁ и d₂ – внутренние диаметры сечений трубы перед и за расширением.

В случае внезапного сужения трубопровода коэффициент местных сопротивлений равен

,

где S₁ и S₂ – площади сечений трубы до и после сужения.

Рекомендации к решению задач

Для решения задачи с применением уравнения Бернулли следует

1. выбрать два сечения, для которых записывается уравнение. В качестве сечений рекомендуется брать:

- выход в атмосферу, где 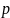_абс = р_а;

- свободную поверхность в резервуаре, где скорость V = 0

- сечение, в котором присоединен прибор для измерения давления (манометр, вакуумметр, пьезометр).

2. записать уравнение Бернулли в общем виде;

3. переписать уравнение для заданных сечений с заменой его членов заданными буквенными величинами и исключить члены, равные нулю.

При этом необходимо помнить:

- уравнение Бернулли записывается по течению жидкости;

- вертикальная ордината z всегда отсчитывается от произвольной горизонтальной плоскости вверх;

- давление р, входящее в правую и левую части уравнения, должно быть задано в одной системе отсчета (абсолютной или избыточной);

- коэффициент Кориолиса в задачах на движение потока реальной жидкости следует учитывать только при ламинарном режиме течения α = 2, для турбулентных потоков можно принимать α = 1;

- суммарная потеря напора записывается в правой части уравнения со знаком «+» и складывается из местных потерь, которые определяются формулой Вейсбаха, и потерь на трение по длине, определяемых формулой Дарси.

Примеры решения задач

П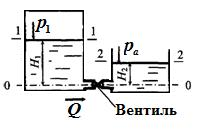 ример 3.1. Горизонтальная труба диаметром d = 5 см соединяет резервуары с водой, в которых поддерживаются постоянные уровни Н₁ = 4,5 м и H₂ = 2,5 м. Для регулирования расхода на трубопроводе установлен вентиль. Определить коэффициент сопротивления вентиля и потерю напора в нем, если расход воды Q = 12,5 л/с, а избыточное давление на поверхности воды в напорном баке р_изб = 25 кПа. Другими потерями напора пренебречь.

Решение:

Перед записью уравнения Бернулли выбираем два сечения.

В качестве начального сечения принимаем открытую поверхность жидкости в напорном баке и обозначаем его 1-1. В пределах этого сечения скорость жидкости мала V₁ ≈ 0, абсолютное давление р₁ = р_а + р_изб. Конечное сечение выбираем на поверхности жидкости в сливном баке 2-2. В пределах этого сечения скорость V₂ ≈ 0, абсолютное давление р₂ = р_а.

В качестве произвольной горизонтальной плоскости для отсчета нивелирных высот (сечение 0-0) выбираем плоскость, совпадающую с осью трубопровода. Тогда z₁ = H₁, а z₂ = H₂.

В соответствии с условием задачи учитываем только местные потери напора на вентиле h_в, тогда уравнение Бернулли принимает вид:

Выразим потери напора на вентиле

С другой стороны, потери напора можно определить по формуле Вейсбаха

Скорость движения жидкости выразим из уравнения неразрывности потока

Подставив в формулу и выразив коэффициент сопротивления, окончательно получаем:

; =

Задачи для практических занятий

Задача 3.1. По трубе диаметром d = 5 см под напором движется минеральное масло. Определить критическую скорость и расход, при которых происходит смена режимов движения жидкости, если температура масла t = 20°C. График зависимости кинематического коэффициента вязкости жидкости от температуры показан на рисунке.

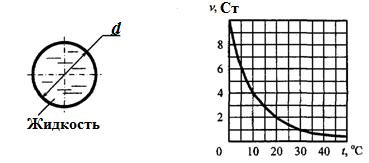
Задача 3.2. Индустриальное масло движется в безнапороном трубопроводе. Трубопровод заполнен наполовину сечения. Диаметр трубопровода d = 0,2 м, кинематический коэффициент вязкости ν = 0,5 см²/с. Определить расход, при котором происходит смена режимов движения жидкости.

Задача 3.3. В гидроприводе допускаемые скорости движения жидкости изменяются от 1,2 до 10 м/с. Определить диапазон изменения числа Рейнольдса при условии: рабочая жидкость – масло индустриальное-12, внутренний диаметр трубопровода d = 10 мм, диапазон изменения рабочих температур от -15 до +55°С.

Задача 3.4. Радиатор системы охлаждения двигателя внутреннего сгорания состоит из пучка трубок диаметром d = 8 мм, по которым протекает вода при температуре t = 90°С. Определить минимальную допустимую среднюю скорость движения воды в трубках при условии, что режим движения должен быть турбулентным.

З адача 3.5. Из напорного бака вода течет по трубе диаметром d₁ = 20 мм и затем вытекает в атмосферу через брандспойт с диаметром выходного отверстия d₂ = 10 мм. Избыточное давление воздуха в баке р₀ = 0,18 МПа; высота Н = 1,6 м. Пренебрегая потерями энергии, определить скорость течения воды в трубе V₁ и на выходе из насадка V₂.

З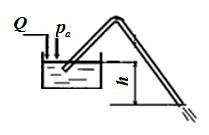 адача 3.6. Определить скорость движения бензина V и расход Q в сифонном трубопроводе. Нижняя точка оси трубопровода расположена ниже уровня жидкости в питающем резервуаре на расстоянии h = 2,5 м. Внутренний диаметр трубопровода d = 25 мм, плотность бензина ρ = 850 кг/м³. Потерями напора пренебречь.

З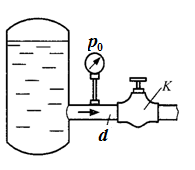 адача 3.7. От бака, в котором с помощью насоса поддерживается постоянное давление жидкости, отходит трубопровод диаметром d = 50 мм. Между баком и краном К на трубопроводе установлен манометр. При закрытом положении крана давление р₀ = 0,5 МПа. Рассчитать расход жидкости Q при полном открытии крана, если манометр показывает р = 0,485 МПа, приняв коэффициент сопротивления входного участка трубопровода (от бака до манометра) равным ζ= 0,5.

Плотность жидкости ρ = 800 кг/м³.

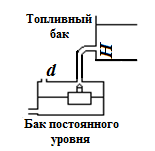
Задача 3.8. Бензин, температура которого 20˚С, перетекает из топливного бака бензопилы в находящийся перед карбюратором бачок постоянного уровня по трубопроводу с внутренним диаметром d = 3 мм. Определить расход бензина Q при напоре H = 0,4 м при полностью открытом поплавковом клапане.

З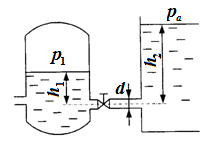 адача 3.9. Вода перетекает из напорного бака, где избыточное давление воздуха р₁ = 0,3 МПа, в открытый резервуар по короткой трубе диаметром d = 50 мм, на которой установлен кран. Чему должен быть равен коэффициент сопротивления крана для того, чтобы расход воды составлял Q = 8,7 л/с? Высоты уровней h₁ = 1 м и h₂ = 3 м. Учесть потерю напора на входе в трубу (внезапное сужение) и на выходе из трубы (внезапное расширение). Потерями на трение пренебречь.

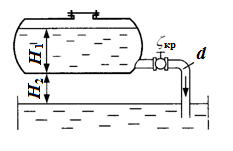З адача 3.10. Бензин сливается из цистерны по трубе диаметром d=50 мм, на которой установлен кран с коэффициентом сопротивления ξ_кр= 3. Определить расход бензина при Н₁ = 1,5 м и Н₂ = 1,3 м, если в верхней части цистерны имеет место вакуум h_вак = 73,5 мм рт. ст. Потерями на трение в трубе пренебречь. Плотность бензина ρ = 750 кг/м³.

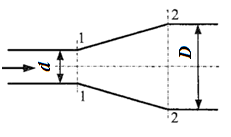
Задача 3.11. Пренебрегая потерями напора, определить степень расширения диффузора n=(D/d)², при котором давление в сечении 2-2 возрастает в два раза по сравнению с давлением в сечении 1-1. Расчет провести при следующих данных: расход жидкости Q = 1,5 л/с; диаметр d = 20 мм; давление в сечении 1-1 р₁ = 10 кПа; плотность жидкости ρ = 1000 кг/м³; режим течения принять: а) ламинарным и б) турбулентным. Поток в диффузоре считать стабилизированным и безотрывным.

З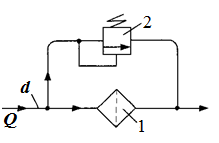 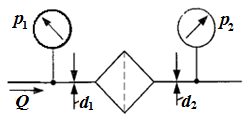адача 3.12. Для определения потерь давления на фильтре установлены манометры, как показано на рисунке. При пропускании через фильтр жидкости, расход которой составляет Q = 1 л/с; манометры показывают р₁ = 0,1 МПа, р₂ = 0,12 МПа. Определить, чему равна потеря давления в фильтре, если известно: d₁ = 10 мм, d₂ = 20 мм, ρ_ж = 900 кг/м³. Потерей давления на участках от мест установки манометров до фильтра пренебречь. Принять α₁ = α₂ = 1.

Задача 3.13. В гидросистеме с расходом масла Q = 0,628 л/с параллельно фильтру 1 установлен переливной клапан 2, открывающийся при перепаде давления на Δp = 0,2 МПа. Определить вязкость ν, при которой начнется открытие клапана, если коэффициент сопротивления фильтра связан с числом Рейнольдса формулой ξ_ф = A/Re, где А = 2640; Re подсчитывается по диаметру трубы d = 20 мм. Плотность масла ρ = 850 кг/м³.

З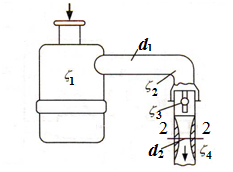 адача 3.14. Воздух засасывается двигателем из атмосферы и проходит через воздухоочиститель и затем по трубе диаметром d₁ = 50 мм подается к карбюратору. Плотность воздуха ρ = 1,28 кг/м³. Определить разрежение в горловине диффузора диаметром d₂ = 25 мм (сечение 2-2) при расходе воздуха Q = 0,05 м³/с. Принять следующие коэффициенты сопротивления: воздухоочистителя ξ₁ = 5, колена ξ₂ = 1, воздушной заслонки ξ₃ = 0,5, сопла ξ₄ = 0,05.

Задача 3.15. Определить напор, создаваемый насосом системы охлаждения автомобильного двигателя, работающего с подачей Q = 3,9 л/с. При решении принять коэффициенты сопротивления блока цилиндров ξ₁ = 3,5, термостата ξ₂ = 2,5, радиатора ξ₃ = 4,0, трубы от радиатора до насоса ξ₄ = 2, сопротивлением трубы от термостата до радиатора пренебречь. Все коэффициенты отнесены к скорости в трубе диаметром d = 40 мм. Чему равно абсолютное давление перед входом в насос, если в верхней части радиатора возник вакуум р_вак = 1 кПа? Принять, что высота уровня жидкости в радиаторе Н = 0,4 м, атмосферное давление соответствует h_а = 750 мм рт.ст., а плотность жидкости ρ = 1000 кг/м³.

Задачи для самостоятельной работы

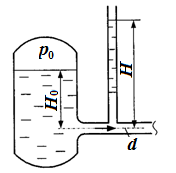
Задача 3с.1. Определить расход жидкости Ж, вытекающей из бака по трубопроводу диаметром d, если избыточное давление воздуха в баке р₀, высота уровня Н₀, высота подъема жидкости в пьезометре, открытом в атмосферу Н. Потерями энергии пренебречь.

Величина	Варианты
	1	2	3	4	5	6	7	8	9	10
Ж	В	Б	К	ДТ	Н	Б	К	ДТ	Б	В
d, мм	60	40	50	30	25	40	50	60	25	50
р0, кПа	12	20	16	10	15	18	14	22	10	17
Н0, м	1,2	0,8	1	1,5	2,5	2	1,2	2,2	0,8	1,3
Н, м	1,8	1,5	1,75	2,2	3,3	2,8	1,9	3,1	1,2	2,1

Обозначения: Б – бензин, В – вода, К – керосин, ДТ –дизельное топливо, Н – нефть.

З адача 3с.2. Определить расход воды в трубе диаметром d₁, имеющей плавное сужение до диаметра d₂, если показания пьезометров: до сужения h₁; в сужении h₂.

Величина	Варианты
	1	2	3	4	5	6	7	8	9	10
d1, мм	100	80	60	150	40	100	80	60	50	100
d2, мм	50	50	30	100	20	40	40	20	20	30
h1, см	90	100	50	100	30	80	90	60	70	100
h2, см	30	40	20	30	10	30	30	20	30	20

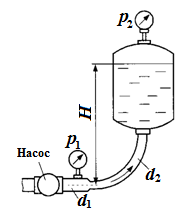
Задача 3с.3. Насос нагнетает жидкость Ж в напорный бак, где установились постоянный уровень на высоте H и постоянное давление р₂. Манометр, установленный на выходе из насоса на трубе диаметром d₁, показывает p₁. Определить расход жидкости Q, если диаметр искривленной трубы, подводящей жидкость к баку, равен d₂; коэффициент сопротивления этой трубы принят равным ζ.

Величина	Варианты
	1	2	3	4	5	6	7	8	9	10
Ж	В	Б	К	ДТ	Н	В	Б	ДТ	К	Н
H, м	2,5	3	1,5	1	2	3,5	2,5	2	1,5	3
p1, МПа	0,3	0,35	0,2	0,1	0,25	0,3	0,25	0,2	0,15	0,25
р2, МПа	0,2	0,3	0,15	0,05	0,2	0,2	0,2	0,1	0,1	0,2
d1, мм	75	65	32	40	75	89	40	65	89	75
d2, мм	50	40	20	25	50	65	25	40	65	50
ζ	0,2	0,3	0,4	0,3	0,5	0,2	0,3	0,4	0,5	0,6

Обозначения: Б – бензин, В – вода, К – керосин, ДТ –дизельное топливо, Н – нефть.

З адача 3с.4. Определить расход жидкости Ж, вытекающей из трубы диаметром d через плавное расширение (диффузор) и далее по трубе диаметром D в бак. Коэффициент сопротивления диффузора ξ_диф (отнесен к скорости в трубе диаметром d), показание манометра p_м; высота h, H. Учесть потери на внезапное расширение, потерями на трение пренебречь, режим течения считать турбулентным.

Величина	Варианты
	1	2	3	4	5	6	7	8	9	10
Ж	В	Б	К	ДТ	Н	Б	К	ДТ	Б	В
d, мм	12	16	18	20	22	24	12	16	18	22
D, мм	16	20	22	24	28	28	18	18	22	24
ξдиф	0,05	0,2	0,1	0,3	0,2	0,25	0,1	0,2	0,15	0,3
pм, кПа	15	20	18	22	20	16	12	14	15	17
h, м	0,3	0,5	0,6	0,4	0,7	0,5	0,8	0,4	0,6	0,5
Н, м	3,5	5	4	5	6	4,5	3	5,5	7	6

Обозначения: Б – бензин, В – вода, К – керосин, ДТ –дизельное топливо, Н – нефть.

З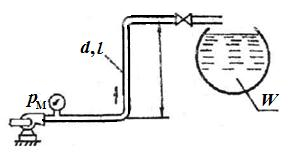 адача 3с.5. По трубопроводу диаметром d насос перекачивает жидкость Ж на высоту Н. Коэффициент сопротивления вентиля ζ = 8. За какое время насос наполнит резервуар емкостью W, если манометр, установленный на выходе из насоса, показывает избыточное давление р_м.

Сопротивлением трубопровода пренебречь.

Величина	Варианты
	1	2	3	4	5	6	7	8	9	10
Ж	В	Б	К	ДТ	Н	Б	К	В	Б	Н
d, мм	80	100	80	60	300	80	100	60	50	200
Н, м	8	15	12	10	80	10	5	20	8	40
W, м3	40	50	100	20	1500	80	50	500	40	1000
pм, кПа	250	300	200	400	1000	150	150	500	250	800

Обозначения: Б – бензин, В – вода, К – керосин, ДТ –дизельное топливо, Н – нефть.