Определения собственного числа, собственного и корневого векторов линейного оператора
Пусть
![]() —
линейное
пространство над полем
—
линейное
пространство над полем
![]() ,
,
![]() —
линейное
преобразование.
—
линейное
преобразование.
Собственным
вектором
линейного преобразования
![]() называется
такой ненулевой вектор
называется
такой ненулевой вектор
![]() ,
что для некоторого
,
что для некоторого
![]()
![]()
Собственным
значением
линейного преобразования
называется
такое число
,
для которого существует собственный
вектор, то есть уравнение
![]() имеет
ненулевое решение
.
имеет
ненулевое решение
.
Упрощённо
говоря, собственный
вектор
— любой ненулевой вектор x, который
отображается оператором в коллинеарный
![]() ,
а соответствующий скаляр
,
а соответствующий скаляр
![]() называется
собственным
значением
оператора.
называется
собственным
значением
оператора.
Собственным
подпространством
линейного преобразования
для
данного собственного числа
(или
отвечающим этому числу) называется
множество всех собственных векторов
,
соответствующих данному собственному
числу (дополненное нулевым вектором).
Обозначим его
![]() .
По определению,
.
По определению,
![]()
где
![]() —
единичный оператор.
—
единичный оператор.
Сложение моментов
Задача на сложение моментов импульса в квантовой механике такова: заданы модули моментов частиц системы; требуется определить допустимые значения модуля и проекций полного момента. Так, в теории многоэлектронных атомов возникает вопрос о нахождении момента импульса электронной оболочки по известным ( из задачи о частице в центральном поле) моментам отдельных электронов. Аналогично ставится вопрос о суммарном спине нескольких электронов в атоме, о спине ядра, состоящего из протонов и нейтронов.
Тогда действия сложения моментов относительно точки производятся алгебраически.
Такая схема сложения моментов называется jj - связью.
Задание последовательности сложения моментов называется генеалогической схемой.
Рассматривая закон сложения моментов нескольких частиц или результирующую четность состояния атома, мы затрагивали вопросы, связанные с задачей многих тел в квантовой механике. Но система, состоящая из одинаковых частиц, обладает в квантовой механике одним совершенно особым свойством, вытекающим из квантовых законов движения. Имеется в виду физическая тождественность одинаковых частиц. Так как проследить за движением каждой из одинаковых частиц невозможно - траектории в квантовой механике отсутствуют, нельзя никаким способом указать состояние некоторого выбранного электрона.
3 Вопрос
Дифракционная решётка
Материал из Википедии — свободной энциклопедии
Перейти к: навигация, поиск
У этого термина существуют и другие значения, см. Решётка.
Очень большая отражательная дифракционная решётка.
Дифракционная решётка — оптический прибор, работающий по принципу дифракции света, представляет собой совокупность большого числа регулярно расположенных штрихов (щелей, выступов), нанесённых на некоторую поверхность. Первое описание явления сделал Джеймс Грегори, который использовал в качестве решётки птичьи перья.
Виды решёток
Отражательные: Штрихи нанесены на зеркальную (металлическую) поверхность, и наблюдение ведется в отражённом свете
Прозрачные: Штрихи нанесены на прозрачную поверхность (или вырезаются в виде щелей на непрозрачном экране), наблюдение ведется в проходящем свете.
Описание явления
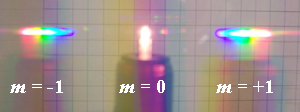
Так выглядит свет лампы накаливания фонарика, прошедший через прозрачную дифракционную решётку. Нулевой максимум (m=0) соответствует свету, прошедшему сквозь решётку без отклонений. В силу дисперсии решётки в первом (m=±1) максимуме можно наблюдать разложение света в спектр. Угол отклонения возрастает с ростом длины волны (от фиолетового цвета к красному)
Фронт световой волны разбивается штрихами решётки на отдельные пучки когерентного света. Эти пучки претерпевают дифракцию на штрихах и интерферируют друг с другом. Так как для разных длин волн максимумы интерференции оказываются под разными углами (определяемыми разностью хода интерферирующих лучей), то белый свет раскладывается в спектр.
Формулы
Расстояние, через которое повторяются штрихи на решётке, называют периодом дифракционной решётки. Обозначают буквой d.
Если
известно число штрихов (![]() ),
приходящихся на 1 мм решётки, то период
решётки находят по формуле:
),
приходящихся на 1 мм решётки, то период
решётки находят по формуле:
![]() мм.
мм.
Условия интерференционных максимумов дифракционной решётки, наблюдаемых под определёнными углами, имеют вид:
![]()
где
![]() —
период
решётки,
—
период
решётки,
![]() —
угол
максимума данного цвета,
—
угол
максимума данного цвета,
![]() —
порядок
максимума, то есть порядковый номер
максимума, отсчитанный от центра
картинки,
—
порядок
максимума, то есть порядковый номер
максимума, отсчитанный от центра
картинки,
— длина волны.
Если
же свет падает на решётку под углом
![]() ,
то:
,
то:
![]()
Характеристики
Одной из характеристик дифракционной решётки является угловая дисперсия. Предположим, что максимум какого-либо порядка наблюдается под углом φ для длины волны λ и под углом φ+Δφ — для длины волны λ+Δλ. Угловой дисперсией решётки называется отношение D=Δφ/Δλ. Выражение для D можно получить если продифференцировать формулу дифракционной решётки
![]()
Таким образом, угловая дисперсия увеличивается с уменьшением периода решётки d и возрастанием порядка спектра k.
Дифракционная решетка как спектрометр
Как
видно из (3.3), положение узких главных
максимумов зависит от длины волны
![]() .
Это позволяет использовать решетку в
качестве спектрального прибора. Решетка
способна разлагать свет в спектр. Для
этого могут быть использованы дифракционные
максимумы различных порядков (кроме
m = 0). Практически, однако, используются
главные максимумы, расположенные в
пределах основного лепестка диаграммы
излучения одиночной щели, имеющего
полуширину
.
Это позволяет использовать решетку в
качестве спектрального прибора. Решетка
способна разлагать свет в спектр. Для
этого могут быть использованы дифракционные
максимумы различных порядков (кроме
m = 0). Практически, однако, используются
главные максимумы, расположенные в
пределах основного лепестка диаграммы
излучения одиночной щели, имеющего
полуширину
![]() .
Отсюда можно получить оценку:
.
Отсюда можно получить оценку:
|
|
(3.5) |
Обычно спектрографы с дифракционной решеткой работают при m = 1 или 2, очень редко при m = 3. Качество решетки как спектрального прибора может быть охарактеризовано рядом параметров. К ним относятся угловая дисперсия, дисперсионная область и разрешающая способность.
Угловая дисперсия.
Угловой дисперсией спектральных приборов принято называть величину
|
|
(3.6) |
В случае решетки, как следует из (3.3), угловая дисперсия равна
|
|
(3.7) |
Приближенное
выражение
![]() справедливо
в случае малых дифракционных углов.
справедливо
в случае малых дифракционных углов.
Дисперсионная область.
Если
спектры соседних порядков перекрываются,
то спектральный прибор становится
непригодным для исследования
соответствующих участков спектра.
Максимальная ширина спектрального
интервала
![]() ,
при которой еще не происходит перекрытия
спектров, называется дисперсионной
областью спектрального прибора.
,
при которой еще не происходит перекрытия
спектров, называется дисперсионной
областью спектрального прибора.
Для случая решетки из (3.3) следует :
|
|
(3.8) |
Как уже было отмечено, в дифракционных решетках используются спектры низких порядков. Поэтому решетки пригодны для исследования широких участков спектра.
Разрешающая способность.
Разрешающей способностью спектрального прибора принято называть отношение
|
|
(3.9) |
где
![]() –
минимальный интервал между двумя
близкими спектральными линиями, при
котором они могут быть разрешены, то
есть отделены одна от другой. В качестве
критерия разрешения используется обычно
критерий разрешения Рэлея. Спектральные
линии с близкими значениями
и
–
минимальный интервал между двумя
близкими спектральными линиями, при
котором они могут быть разрешены, то
есть отделены одна от другой. В качестве
критерия разрешения используется обычно
критерий разрешения Рэлея. Спектральные
линии с близкими значениями
и
![]() считаются
разрешенными, если главный максимум
дифракционной картины для одной
спектральной линии совпадает по своему
положению с первым дифракционным
минимумом для другой спектральной
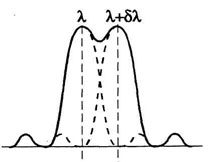
линии. Рис. 3.4. поясняет критерий
Рэлея.
считаются
разрешенными, если главный максимум
дифракционной картины для одной
спектральной линии совпадает по своему
положению с первым дифракционным
минимумом для другой спектральной
линии. Рис. 3.4. поясняет критерий
Рэлея.
|
Рисунок 3.4. Кретерий спектрального разрешения Рэлея. |
Так как спектральные линии, изображенные на рис. 3.4, некогерентны, результирующая интенсивность равна сумме интенсивностей (сплошная кривая на рис. 3.4). Наличие провала в центре кривой распределения интенсивности указывает на условный характер критерия Рэлея.
Для разрешающей способности дифракционной решетки легко получить из выражения (3.3):
|
|
Угловая дисперсия и разрешающая способность решетки
Угловая дисперсия дифракционной решетки:
 где
δ. - угловое расстояние между двумя
спектральными линиями с разностью длин
волн δλ, "фи" - угол дифракции,
k=1,2,3...
где
δ. - угловое расстояние между двумя
спектральными линиями с разностью длин
волн δλ, "фи" - угол дифракции,
k=1,2,3...
Разрешающая способность решетки (вывод с использованием критерия Релея).
Разрешающей
способностью спектрального при¬бора
назовем безразмерную величину
![]() ,
где
,
где
![]() -
абсолютное значение минимальной разности
длин волн двух соседних спектральных
линий, при которой эти линии регистрируются
раздельно. Пусть максимум m-го порядка
для длины волны
-
абсолютное значение минимальной разности
длин волн двух соседних спектральных
линий, при которой эти линии регистрируются
раздельно. Пусть максимум m-го порядка
для длины волны
![]() наблюдается
под углом
наблюдается
под углом
![]() ,
т.е.
,
т.е.
![]() .
При переходе от максимума к соседнему
минимуму, разность хода меняется на
.
При переходе от максимума к соседнему
минимуму, разность хода меняется на
![]() ,
где N – число щелей решетки. Следовательно
минимум
,
где N – число щелей решетки. Следовательно
минимум
![]() ,
наблюдаемый под углом
,
наблюдаемый под углом
![]() ,
удовлетворяет условию
,
удовлетворяет условию
![]() .
По критерию Релея (Изображения двух
близлежащих одинаковых точечных
источников или двух близлежащих
спектральных линий с равными интенсивностями
и одинаковыми симметричными контурами
раз¬решимы (разделены для восприятия),
если цен¬тральный максимум дифракционной
картины от одного источника (линии)
совпадает с первым минимумом дифр.
картины от другого),
.
По критерию Релея (Изображения двух
близлежащих одинаковых точечных
источников или двух близлежащих
спектральных линий с равными интенсивностями
и одинаковыми симметричными контурами
раз¬решимы (разделены для восприятия),
если цен¬тральный максимум дифракционной
картины от одного источника (линии)
совпадает с первым минимумом дифр.
картины от другого),
![]() или
или
![]() .
т.к.
.
т.к.
![]() и
и
![]() близки
между собой, т.е.
близки
между собой, т.е.
![]() ,
то согласно
,
то согласно
![]() :
:
![]() .
Таким образом разр. способность дифр
решетки пропорцио¬нальна порядку m
спектров и числу Nщелей, т.е. при заданном
N увеличивается при переходе к спектрам
высших порядков. Современные ре¬шетки
обладают разр способностью до 2*10в5.
.
Таким образом разр. способность дифр
решетки пропорцио¬нальна порядку m
спектров и числу Nщелей, т.е. при заданном
N увеличивается при переходе к спектрам
высших порядков. Современные ре¬шетки
обладают разр способностью до 2*10в5.