Математическое определение

Сила Кориолиса равна:

,

где   — точечная масса,   — вектор угловой скорости вращающейся системы отсчёта,   — вектор скорости движения точечной массы в этой системе отсчёта, квадратными скобками обозначена операция векторного произведения.

Величина   называется кориолисовым ускорением.

[Править]Правило Жуковского

Н. Е. Жуковским была предложена удобная для практического использования словесная формулировка определения силы Кориолиса

Ускорение Кориолиса   можно получить, спроецировав вектор скорости материальной точки в неинерциальной системе отсчёта   на плоскость, перпендикулярную вектору угловой скорости неинерциальной системы отсчёта  , увеличив полученную проекцию в   раз и повернув её на 90 градусов в направлении переносного вращения.

[Править]Получение

Пусть тело совершает сложное движение: движется относительно неинерциальной системы отсчёта S' со скоростью   S' при этом сама движется поступательно с абсолютной линейной скоростью   и одновременно вращается с угловой скоростью   в инерциальной системе координат S.

Тогда линейная скорость тела в неподвижной инерциальной системе координат равна:

, причем 

где   — радиус-вектор центра масс тела относительно неинерциальной системы отсчета S'. Продифференцируем данное уравнение:

Найдём значение каждого слагаемого в инерциальной системе координат:

где   — линейное ускорение тела относительно системы S' в предположении ее неподвижности,   — угловое ускорение системы S' .

Таким образом, получаем:

Слагаемое   и будет кориолисовым ускорением, образованном от взаимного влияния переносного поворотного и относительного поступательного движений.

Заметим, что если система S также является неинерциальной и движется относительно другой системы, а та другая относительно следующей и т. д., то величины   ,   для системы S' в последнем уравнении следует считать полными — то есть как сумму собственных ускорений (скоростей) всех систем координат (каждой относительно предыдущей), начиная с первой подвижной системы, а   — абсолютным ускорением поступательного движения S' относительно неподвижной инерциальной системы координат.

Заметим также, что в частности, чтобы тело относительно неинерциальной системы отсчета двигалось прямолинейно по радиусу к оси вращения (см. рис.), необходимо приложить к нему силу, которая будет противодействующей суммы Кориолисовой силы   , переносной вращательной силы   и переносной силы инерции поступательного движения системы отсчета   . Составляющая же ускорения   не отклонит тело от этой прямой так как является осестремительным переносным ускорением и всегда направлена по этой прямой. Действительно, если рассматривать уравнение такого движения, то после компенсации в нем вышеупомянутых сил получится уравнение  , которое если умножить векторно на  , то с учетом   получим относительно   дифур 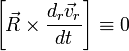 , имеющий при любых   и   общим решением  , которое и является уравнением такой прямой —   .

[Править]Физический смысл

Пусть тело движется со скоростью   вдоль прямой к центру координат инерциальной системы отсчёта (см. рис.).

Тогда данное движение приведёт к изменению расстояния до центра вращения   и, как следствие, абсолютной скорости движения точки неинерциальной системы отсчёта, совпадающей с движущейся точкой - ее переносной скорости.

Как мы знаем, эта скорость движения равна 

Данное изменение будет равно:

Проведя дифференцирование по времени, получим   (направление данного ускорения перпендикулярно   и  ).

С другой стороны, вектор   для точки, остающейся неподвижной относительно инерциального пространства, повернётся относительно неинерциального на угол  . Или приращение скорости будет

 при   соответственно второе ускорение будет:

Общее ускорение будет   Как видно, система отсчёта не претерпела изменения угловой скорости   Линейная скорость относительно неё не меняется и остаётся   Тем не менее, ускорение не равно нулю.

Если тело движется перпендикулярно направлению к центру вращения, то доказательство будет аналогичным. Ускорение из-за поворота вектора скорости останется   а также прибавляется ускорение в результате изменения центростремительного ускорения точки.