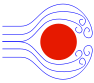
Переход к турбулентности

Ламинарное течение возможно только до некоторого критического значения числа Рейнольдса, после которого оно переходит в турбулентное. Критическое значение числа Рейнольдса зависит от конкретного вида течения (течение в круглой трубе, обтекание шара и т. п.). Например, для течения в круглой трубе  .

Турбуле́нтность, устар. турбуле́нция (от лат. turbulentus — бурный, беспорядочный), турбуле́нтное тече́ние — явление, заключающееся в том, что при увеличении скорости течения жидкости или газа в среде самопроизвольно образуются многочисленные нелинейные фрактальные волны и обычные, линейные различных размеров, без наличия внешних, случайных, возмущающих среду сил и/или при их присутствии. Для расчёта подобных течений были созданы различные модели турбулентности. Волны появляются случайно. То есть их размер и амплитуда меняется хаотически в некотором интервале. Они возникают чаще всего либо на границе, у стенки, и/или при разрушении или опрокидывании волны. Они могут образоваться на струях. Экспериментально ее можно наблюдать на конце струи пара из электрочайника. Турбулентность экспериментально открыта английским инженером Рейнольдсом в 1883 году при изучении течения несжимаемой жидкости (воды) в трубах.

Для возникновения турбулентности необходима сплошная среда, которая подчиняется кинетическому уравнению Больцмана, Навье — Стокса или пограничного слоя. Уравнение Навье — Стокса (в него входит и уравнение сохранения массы или уравнение неразрывности) описывает множество турбулентных течений с достаточной для практики точностью.

Обычно турбулентность наступает при превышении некоторого критического параметра, например числа Рейнольдса или Релея (в частном случае скорости потока при постоянной плотности и диаметре трубы и/или температуры на внешней границе среды).

При определённых параметрах турбулентность наблюдается в потоках жидкостей и газов, многофазных течениях, жидких кристаллах, квантовых Бозе- и Ферми- жидкостях, магнитных жидкостях,плазме и любых сплошных средах (например, в песке, земле, металлах). Турбулентность также наблюдается при взрывах звёзд, в сверхтекучем гелии, в нейтронных звёздах, в лёгких человека, движении крови в сердце, при турбулентном (т. н. вибрационном) горении.

Турбулентность возникает самопроизвольно, когда соседние области среды следуют рядом или проникают один в другой, при наличии перепада давления или при наличии силы тяжести, или когда области среды обтекают непроницаемые поверхности. Она может возникать при наличии вынуждающей случайной силы. Обычно внешняя случайная сила и сила тяжести действуют одновременно. Например, при землетрясении или порыве ветра падает лавина с горы, внутри которой течение снега турбулентно. Мгновенные параметры потока (скорость, температура, давление, концентрация примесей) при этом хаотично колеблются вокруг средних значений. Зависимость квадрата амплитуды от частоты колебаний (или спектр Фурье) является непрерывной функцией.

Турбулентность, например, можно создать:

• увеличив число Рейнольдса (увеличить линейную скорость или угловую скорость вращения потока, размер обтекаемого тела, уменьшить первый или второй коэффициент молекулярной вязкости, увеличить плотность среды);

• увеличив число Релея (нагреть среду);

• увеличить число Прандтля (уменьшить вязкость);

• задать очень сложный вид внешней силы (примеры: хаотичная сила, удар). Течение может не иметь фрактальных свойств.

• создать сложные граничные или начальные условия, задав функцию формы границ. Например, их можно представить случайной функцией. Например: течение при взрыве сосуда с газом. Можно, например, организовать вдув газа в среду, создать шероховатую поверхность. Использовать разгар сопла. Поставить сетку в течение. Течение может при этом не иметь фрактальных свойств.

• создать квантовое состояние. Данное условие применимо только к изотопу гелия 3 и 4. Все остальные вещества замерзают, оставаясь в нормальном, не квантовом состоянии.

• облучить среду звуком высокой интенсивности.

• с помощью химических реакций, например горения. Форма пламени, как и вид водопада может быть хаотичной.

Лобовое сопротивление — сила, препятствующая движению тел в жидкостях и газах. Лобовое сопротивления складывается из двух типов сил: сил касательного (тангенциального) трения, направленных вдоль поверхности тела, и сил давления, направленных по нормали к поверхности. Сила сопротивления является диссипативной силой и всегда направлена против вектора скорости тела в среде. Наряду с подъёмной силой является составляющей полной аэродинамической силы.

Сила лобового сопротивления обычно представляется в виде суммы двух составляющих: сопротивления при нулевой подъёмной силе и индуктивного сопротивления. Каждая составляющая характеризуется своим собственным безразмерным коэффициентом сопротивления и определённой зависимостью от скорости движения.

Лобовое сопротивление может способствовать как обледенению летательных аппаратов (при низких температурах воздуха), так и вызывать нагревание лобовых поверхностей ЛА при сверхзвуковых скоростях ударной ионизацией.

Поток и форма препятствия	Профильное сопротивление	Сопротивление обшивки
	0 %	100 %
	~10 %	~90 %
	~90 %	~10 %
	100 %	0 %

Подъёмная сила — составляющая полной аэродинамической силы, перпендикулярная вектору скорости движения тела в потоке жидкости или газа, возникающая в результате несимметричности обтекания тела потоком. В соответствии с законом Бернулли, статическое давление среды в тех областях, где скорость потока более высока, будет ниже, и наоборот. Например, крыло самолета имеет несимметричный профиль (верхняя часть крыла более выпуклая), вследствие чего скорость потока по верхней кромке крыла будет выше, чем над нижней. Создавшаяся разница давлений и порождает подъёмную силу. Полная аэродинамическая сила — это интеграл от давления вокруг контура крыла.

где:

• Y — это подъёмная сила,

• P — это тяга,

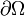•  — граница профиля,

• p — величина давления,

• n — нормаль к профилю

Согласно теореме Жуковского, величина подъёмной силы пропорциональна плотности среды, скорости потока и циркуляции скорости потока.

Коэффициент подъёмной силы — безразмерная величина, характеризующая подъемную силу крыла определённого профиля при известном угле атаки. Коэффициент определяется экспериментальным путём в аэродинамической трубе, либо по теореме Жуковского. Формулу расчёта подъёмной силы через коэффициент разработали братья Райт и Джон Смитон в начале XX века. Формула имеет вид^[1]:

где:

 — подъёмная сила (Н)

 — коэффициент подъёмной силы

 — весовая плотность воздуха на высоте полёта (кг/м³)

 — скорость набегающего потока (м/с)

 — характерная площадь (м²)

При расчетах по этой формуле важно не путать весовую и массовую плотность воздуха. Весовая плотность при стандартных атмосферных условиях (на уровне земли при температуре +15 С) равна  =1.225 кг/м³. Но в аэродинамических расчетах часто используют массовую плотность воздуха, которая равна 0.125 кг*с²/м⁴. В этом случае подъемная сила Y получается не в ньютонах (Н), а в килограммах (кг). В книгах по аэродинамике не всегда имеются уточнения, о какой плотности и размерности подъемной силы идет речь, поэтому в спорных ситуациях нужно проверять формулы, сокращая единицы измерения.

11. Неинерциальные системы отсчета. Силы инерции в прямолинейно движущихся и равномерно вращающихся неинерциальных системах отсчета.

Неинерциальная система отсчёта — система отсчёта, к которой не применим закон инерции (говорящий о том, что каждое тело, в отсутствие действующих на него сил, движется по прямой и с постоянной скоростью), и поэтому для согласования сил и ускорений в которой приходится вводить фиктивные силы инерции. Всякая система отсчета, движущаяся с ускорением относительно инерциальной, является неинерциальной. Неинерциальными называются системы, движущиеся ускоренно, в том числе вращающиеся (т.к. тело, движущееся по окружности, испытывает центростремительное ускорение).

(X’’- икс с двумя точками)

Пусть система x′, y′ (автомобиль, например) движется ускоренно в

лабораторной системе (рис. 3.1). Это означает, что в лабораторной системе

mx’’ ≡ ma = F, где F – сила, вызывающая ускорение. В системе автомобиля любое тело

подчиняется уравнению

mx’’′ = F′ ; но x’ = x’′ +V , откуда x’’ = x’’′ + a .

Следовательно,

Mx’’′ = mx’’− ma = F − ma = F′.

Таким образом, в системе ускорения движущегося автомобиля на тело кроме

силы F действует еще сила – ma, именуемая инерционной силой, или силой

инерции.

Центробежная сила инерции во вращающейся

системе координат

Рассмотрим простой пример: кубик покоится на диске, вращающемся с

угловой скоростью Ω (рис. 3.3); k − коэффициент трения. Уравнение движения

кубика в лабораторной системе (см. (1.6)) имеет вид

mar ≡ m(r’’−Ω2r)= kmg,

где Ω^2 r – центростремительное ускорение. Сила трения направлена против

направления скорости при смещении кубика. Отсюда

mr’’ = mr’’′ = mΩ^2r + kmg.

Таким образом, во вращающейся системе появляется центробежная сила

инерции FЦБСИ, равная по модулю произведению массы на центростремительное

ускорение в лабораторной системе и направленная вдоль радиуса наружу от оси

вращения:

F m r. ЦБСИ

= Ω2 (3.1)

Кубик не смещается, если k > Ω^2r/g.

12. Сила инерции Кориолиса. Проявление сил инерции на земле. Маятник Фуко.

+PDF

Си́ла Кориоли́са — одна из сил инерции, существующая в неинерциальной системе отсчёта из-за вращения и законов инерции, проявляющаяся при движении в направлении под углом к оси вращения. Названа по имени французского учёного Гюстава Гаспара Кориолиса, впервые её описавшего. Ускорение Кориолиса было получено Кориолисом в 1833 году, Гауссом в 1803 году иЭйлером в 1765 году.

Причина появления силы Кориолиса — в кориолисовом (поворотном) ускорении. В инерциальных системах отсчёта действует закон инерции, то есть, каждое тело стремится двигаться по прямой и с постоянной скоростью. Если рассмотреть движение тела, равномерное вдоль некоторого вращающегося радиуса и направленное от центра, то станет ясно, что чтобы оно осуществилось, требуется придавать телу ускорение, так как чем дальше от центра, тем должна быть больше касательная скорость вращения. Это значит, что с точки зрения вращающейся системы отсчёта, некая сила будет пытаться сместить тело с радиуса.

Для того, чтобы тело двигалось с кориолисовым ускорением, необходимо приложение силы к телу, равной  , где   — кориолисово ускорение. Соответственно, тело действует по третьемузакону Ньютона с силой противоположной направленности.   Сила, которая действует со стороны тела, и будет называться силой Кориолиса. Не следует путать Кориолисову силу с другой силой инерции — центробежной силой, которая направлена по радиусу вращающейся окружности.

Если вращение происходит по часовой стрелке, то двигающееся от центра вращения тело будет стремиться сойти с радиуса влево. Если вращение происходит против часовой стрелки — то вправо.

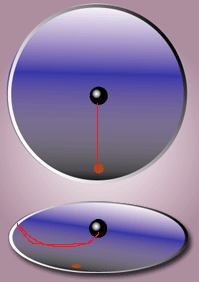
При вращении диска более далёкие от центра точки движутся с большей касательной скоростью, чем менее далёкие (группа чёрных стрелок вдоль радиуса). Переместить некоторое тело вдоль радиуса так, чтобы оно оставалось на радиусе (синяя стрелка из положения «А» в положение «Б») можно, увеличив скорость тела, то есть придав ему ускорение. Еслисистема отсчёта вращается вместе с диском, то видно, что тело «не хочет» оставаться на радиусе, а «пытается» уйти влево — это и есть сила Кориолиса.