Недостатки ньютоновской модели тяготения

Практика показала, что классический закон всемирного тяготения позволяет с огромной точностью объяснить и предсказать движения небесных тел. Однако ньютоновская теория содержала ряд серьёзных недостатков. Главный из них — необъяснимое дальнодействие: сила притяжения передавалась неизвестно как через совершенно пустое пространство, причём бесконечно быстро. По существу ньютоновская модель была чисто математической, без какого-либо физического содержания. Кроме того, если Вселенная, как тогда предполагали, евклидова и бесконечна, и при этом средняя плотность вещества в ней ненулевая, то возникает гравитационный парадокс: потенциал поля всюду обращается в бесконечность. В конце XIX века обнаружилась ещё одна проблема: заметное расхождение теоретического и наблюдаемого смещения перигелия Меркурия.

На протяжении более двухсот лет после Ньютона физики предлагали различные пути усовершенствования ньютоновской теории тяготения. Эти усилия увенчались успехом в 1915 году, с созданием общей теории относительностиЭйнштейна, в которой все указанные трудности были преодолены. Теория Ньютона оказалась приближением более общей теории, применимым при выполнении двух условий:

Гравитационный потенциал в исследуемой системе не слишком велик (много меньше ).
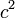Скорости движения в этой системе незначительны по сравнению со скоростью света.

Гравитационное поле в общей теории относительности

Основная статья: Общая теория относительности

В общей теории относительности (ОТО) гравитационное поле является не отдельным физическим понятием, а свойством пространства-времени, появляющимся в присутствии материи. Этим свойством является неевклидовость метрики(геометрии) пространства-времени, и материальным носителем тяготения является пространство-время. Тот факт, что гравитацию можно рассматривать как проявление свойств геометрии четырёхмерного неевклидова пространства, без привлечения дополнительных понятий, есть следствие того, что все тела в поле тяготения получают одинаковое ускорение («принцип эквивалентности» Эйнштейна). Пространство-время при таком подходе приобретает физические атрибуты, которые влияют на физические объекты и сами зависят от них.

Пространство-время ОТО представляет собой псевдориманово многообразие с переменной метрикой. Причиной искривления пространства-времени является присутствие материи, и чем больше её энергия, тем искривление сильнее. Для определения метрики пространства-времени при известном распределении материи надо решить уравнения Эйнштейна. Ньютоновская же теория тяготения представляет собой приближение ОТО, которое получается, если учитывать только «искривление времени», то есть изменение временно́й компоненты метрики, ^[2] (пространство в этом приближении евклидово). Распространение возмущений гравитации, то есть изменений метрики при движении тяготеющих масс, происходит с конечной скоростью, и дальнодействие в ОТО отсутствует.

Другие существенные отличия гравитационного поля ОТО от ньютоновского: возможность нетривиальной топологии пространства, особых точек, гравитационные волны.

35. Напряженность и потенциал поля тяготения.

Определим работу, которую совершают силы поля тяготения при перемещении в поле материальной точки массой m. Вычислим, какую надо затратить работу для удаления тела массой m от Земли. На расстоянии R (рис. 1) на тело действует сила

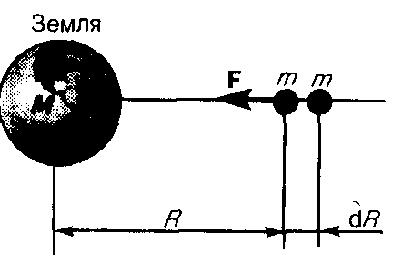
Рис.1

При перемещении этого тела на расстояние dR совершается работа (1) Знак минус появляется потому, что сила и перемещение в данном случае противоположны по направлению (рис. 1). Если тело перемещать с расстояния R₁ до R₂, то работа (2) Из формулы (2) следует, что затраченная работа в поле тяготения не зависит от траектории перемещения, а зависит лишь от начального и конечного положения тела, т. е. силы тяготения действительно консервативны, а поле тяготения являетсяпотенциальным. Работа, совершаемая консервативными силами, равна изменению потенциальной энергии системы, взятому со знаком минус, т. е. Из формулы (2) получаем (3) Так как в формулы входит только разность потенциальных энергий в двух состояниях, то для удобства принимают потенциальную энергию при R₂→∞ равной нулю (P₂=0). Тогда (3) запишется в виде P₁= -GmM/R₁. Поскольку первую точку мы выбрали произвольно, то Величина является энергетической характеристикой поля тяготения и называется потенциалом. Потенциал поля тяготения φ - скалярная величина, которая определяется потенциальной энергией тела единичной массы в данной точке поля или работой по перемещению единичной массы из данной точки поля в бесконечность. Таким образом, потенциал поля тяготения, создаваемого телом массой М, равен (4) где R - расстояние от этого тела до рассматриваемой точки. Из формулы (4) следует, что геометрическое место точек с равными потенциалами образует сферическую поверхность (R=const). Такие поверхности, для которых потенциал постоянен, называются эквипотенциальными. Исследуем взаимосвязь между потенциалом φ поля тяготения и его напряженностью g. Из выражений (1) и (4) вытекает, что элементарная работа dA, совершаемая силами поля при малом перемещении тела массой m, равна С другой стороны, dA=Fdl (dl - элементарное перемещение). Учитывая (24.1), полу¬чаем, что dA=mgdl, т. е. mgdl= -mdφ, или Величина dφ/dl характеризует изменение потенциала на единицу длины в направлении перемещения в поле тяготения. Можно показать, что (5) где - градиент скаляра φ. Знак минус в формуле (5) показывает, что вектор напряженности g направлен в сторону убывания потенциала. В качестве частного примера, исходя из представлений теории тяготения, рассмотрим потенциальную энергию тела, находящегося на высоте h относительно Земли: где R₀ - радиус Земли. Так как и то, учитывая условие h<<R₀, получаем