Вывод закона Архимеда для тела произвольной формы

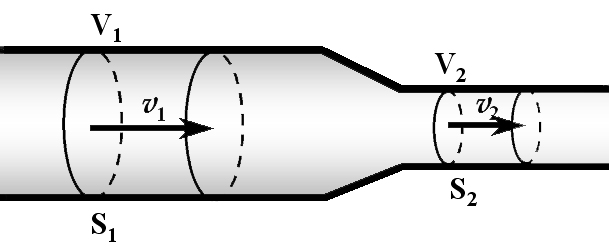
Уравнение неразрывности струи.

Рассмотрим стационарный (скорость в данной точке не изменяется со временем) поток идеальной (нет внутреннего трения) несжимаемой жидкости.  В этом случае выполняется закон сохранения массы.

Пусть за время t через сечение трубы S₁ проходит жидкость массой m₁ (рис. 2.3):    Тогда через сечение S₂ за тоже время проходит жидкость массой m₂:    Так как m₁=m₂, то   или    Где сечение трубы меньше, там скорость жидкости больше, и наоборот (если S₁ > S₂, то v₁ < v₂).

Классическое уравнение Эйлера

Рассмотрим движение идеальной жидкости. Выделим внутри неё некоторый объём V. Согласно второму закону Ньютона, ускорение центра масс этого объёма пропорционально полной силе, действующей на него. В случае идеальной жидкости эта сила сводится к давлению окружающей объём жидкости и, возможно, воздействию внешних силовых полей. Предположим, что это поле представляет собой силы инерции илигравитации, так что эта сила пропорциональна напряжённости поля и массе элемента объёма. Тогда

,

где S — поверхность выделенного объёма, g — напряжённость поля. Переходя, согласно формуле Гаусса — Остроградского, от поверхностного интеграла к объёмному и учитывая, что  , где   — плотность жидкости в данной точке, получим:

В силу произвольности объёма V подынтегральные функции должны быть равны в любой точке:

Выражая полную производную через конвективную производную и частную производную:

получаем уравнение Эйлера для движения идеальной жидкости в поле тяжести:

где   — плотность жидкости,  — давление в жидкости,  — вектор скорости жидкости,  — вектор напряжённости силового поля,  — оператор набла для трёхмерного пространства.

9. Уравнение Бернулли. Формула Торричелли. Реакция вытекающей струи.

Закон Бернулли является следствием закона сохранения энергии для стационарного потока идеальной (то есть без внутреннего трения) несжимаемой жидкости:

Здесь

 — плотность жидкости,

 — скорость потока,

 — высота, на которой находится рассматриваемый элемент жидкости,

 — давление в точке пространства, где расположен центр массы рассматриваемого элемента жидкости,

 — ускорение свободного падения.

Константа в правой части обычно называется напором, или полным давлением, а также интегралом Бернулли. Размерность всех слагаемых — единица энергии, приходящаяся на единицу объёма жидкости.

Это соотношение, выведенное Даниилом Бернулли в 1738 г., было названо в его честь уравнением Бернулли (не следует путать с дифференциальным уравнением Бернулли).

Для горизонтальной трубы   и уравнение Бернулли принимает вид:    .

Эта форма уравнения Бернулли может быть получена путём интегрирования уравнения Эйлера для стационарного одномерного потока жидкости, при постоянной плотности  :    .

Согласно закону Бернулли, полное давление в установившемся потоке жидкости остается постоянным вдоль этого потока.

Полное давление состоит из весового  , статического   и динамического   давлений.

Из закона Бернулли следует, что при уменьшении сечения потока, из-за возрастания скорости, то есть динамического давления, статическое давление падает. Это является основной причиной эффекта Магнуса. Закон Бернулли справедлив и для ламинарных потоков газа. Явление понижения давления при увеличении скорости потока лежит в основе работы различного рода расходомеров (например труба Вентури), водо- и пароструйных насосов. А последовательное применение закона Бернулли привело к появлению технической гидромеханической дисциплины — гидравлики.

Закон Бернулли справедлив в чистом виде только для жидкостей, вязкость которых равна нулю, то есть таких жидкостей, которые не прилипают к поверхности трубы. На самом деле экспериментально установлено, что скорость жидкости на поверхности твердого тела почти всегда в точности равна нулю (кроме случаев отрыва струй при некоторых редких условиях).

Одно из применений

Закон Бернулли можно применить к истечению идеальной несжимаемой жидкости через малое отверстие в боковой стенке или дне широкого сосуда.

(рис 2.3)