[Править]Свойства преобразований Лоренца

• Можно заметить, что в случае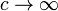, когда  , преобразования Лоренца переходят в преобразования Галилея. То же самое происходит в случае, когда 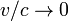 . Это говорит о том, что специальная теория относительности совпадает с механикой Ньютона либо в мире с бесконечной скоростью света, либо при скоростях, малых по сравнению со скоростью света. Последее объясняет, каким образом сочетаются эти две теории — первая является обобщением и уточнением второй, а вторая — предельным случаем первой, оставаясь в этом качестве верной приближенно (с некоторой точностью, на практике часто очень и очень большой) при достаточно малых (по сравнению со скоростью света) скоростях движений.

• Преобразования Лоренца сохраняют инвариантным интервал для любой пары событий (точек пространства-времени) — то есть любой пары точек пространства-времени Минков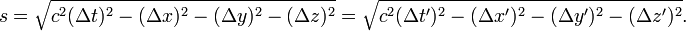ского: Убедиться в этом нетрудно, например, проверив явно то, что матрица преобразования Лоренца   ортогональна в смысле метрики Минковского 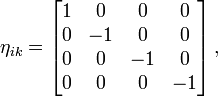определяемой таким выражением, то есть 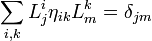 . Это проще всего проделать для буста, а для трехмерных вращений это очевидно из определения декартовых координат, кроме того, сдвиги начала отсчёта не меняют разностей координат. Следовательно, это свойство верно и для любых композиций бустов, вращений и сдвигов, что и составляет полную группу Пуанкаре; как только мы узнали, что преобразования координат ортогональны, из этого сразу следует, что формула для расстояния остаётся неизменной при переходе к новой системе координат — по определению ортогональных преобразований.

• В частности, инвариантность интервала имеет место и для случая 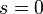 , а значит — гиперповерхность в пространстве-времени, которая определяется равенством нулю интервала до заданной точки — световой конус — является неподвижной при преобразованиях Лоренца (что является проявлением инвариантности скорости света). Внутреность двух полостей конуса соответствует времениподобным — вещественным — интервалам от их точек до вершины, внешняя область — пространственноподобным — чисто мнимым (в принятой в этой статье сигнатуре интервала).

• Другие инвариантные гиперповерхности однородных преобразований Лоренца (аналоги сферы для пространства Минковского) — гиперболоиды: двуполостный гиперболоид для времениподобных интервалов относительно начала координат, и однополостный — для пространственноподобных интервалов.

• Матрицу преобразования Лоренца при коллинеарных пространственных осях (в системе единиц c=1) можно представить как:

где  . В этом легко убедиться, учитывая   и проверив выполнение соответствующего тождества для матрицы преобразования Лоренца в обычном виде.

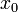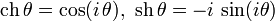• Если принять введённые Минковским обозначения  , то преобразование Лоренца для такого пространства сводится к повороту на мнимый угол в плоскости, включающей ось   (для случая движения вдоль оси   — в плоскости  ). Это очевидно, исходя из подстановки   в матрицу, приведенную чуть выше — и её небольшого изменения для того, чтобы учесть вводимую мнимость временной координаты — и сравнении её с обычной матрицей вращения.