Преобразования Лоренца в физике
Преобразованиями
Лоренца в физике, в частности, в специальной
теории относительности (СТО),
называются преобразования, которым
подвергаются пространственно-временные
координаты 
каждого
события при переходе от одной инерциальной
системы отсчета (ИСО) к
другой. Аналогично, преобразованиям
Лоренца при таком переходе подвергаются
координаты любого 4-вектора.
Чтобы явно различить преобразования Лоренца со сдвигами начала отсчёта и без сдвигов, когда это необходимо, говорят о неоднородных и однородных преобразованиях Лоренца.
Преобразования Лоренца без сдвигов начала отсчёта образуют группу Лоренца, со сдвигами — группу Пуанкаре, иначе называемую неоднородной группой Лоренца.
С математической точки зрения преобразования Лоренца — это преобразования, сохраняющие неизменной метрику Минковского, то есть, в частности, последняя сохраняет при них простейший вид при переходе от одной инерциальной системы отсчёта к другой (другими словами преобразования Лоренца — это аналог для метрики Минковского ортогональных преобразований, осуществляющих переход от одного ортонормированного базиса к другому, то есть аналог поворота координатных осей для пространства-времени). В математике или теоретической физике преобразования Лоренца могут относиться к любой размерности пространства.
Именно преобразования Лоренца, смешивающие — в отличие от преобразований Галилея — пространственные координаты и время, исторически стали основой для формирования концепции единого пространства-времени.
Следует заметить, что лоренц-ковариантны не только фундаментальные уравнения (такие, как уравнения Максвелла, описывающее электромагнитное поле, уравнение Дирака, описывающее электрон и другие фермионы), но и такие макроскопические уравнения, как волновое уравнение, описывающее (приближенно) звук, колебания струн и мембран, и некоторые другие (только тогда уже в формулах преобразований Лоренца под c следует иметь в виду не скорость света, а какую-то другую константу, например скорость звука). Поэтому преобразования Лоренца могут быть плодотворно использованы и в связи с такими уравнениями (хотя и в довольно формальном смысле, впрочем, мало отличающемся — в своих рамках — от их применения в фундаментальной физике).
[Править]Вид преобразований при коллинеарных (параллельных) пространственных осях
Если
ИСО 
движется
относительно ИСО 
с
постоянной скоростью
вдоль
оси
,
а начала
пространственных координат совпадают
в начальный момент времени в обеих
системах, то преобразования Лоренца
(прямые) имеют вид:
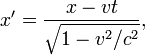
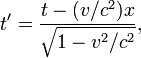
где — скорость света, величины со штрихами измерены в системе , без штрихов — в .
Эта форма преобразования (то есть при выборе коллинеарных осей), называемая иногда бустом (англ. boost) или лоренцевским бустом (особенно в англоязычной литературе), несмотря на свою простоту, включает, по сути, всё специфическое физическое содержание преобразований Лоренца, так как пространственные оси всегда можно выбрать таким образом, а при желании добавить пространственные повороты не представляет трудности (см. это в явном развёрнутом виде ниже), хотя и делает формулы более громоздкими.
Формулы, выражающие обратное преобразование, то есть выражающие
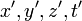через 
можно
получить просто заменой
на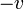 
(абсолютная
величина относительной скорости
движения систем отсчёта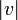 
одинакова
при измерении её в обеих системах
отсчёта, поэтому можно при желании
снабдить
штрихом,
только при этом надо внимательно следить
за тем, чтобы знак и определение
соответствовали друг другу) и взаимной
заменой штрихованных
и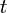 
с
нештрихованными. Или решая систему
уравнений (1) относительно
.Надо иметь в виду, что в литературе преобразования Лоренца часто записывается для упрощения в системе единиц, где
,
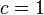что действительно делает их вид более
изящным.Видно, что при преобразованиях Лоренца события, одновременные в одной системе отсчёта, не являются одновременными в другой (относительность одновременности), кроме того, у движущегося тела сокращается продольный размер по сравнению с тем, какой оно имеет в сопутствующей ему системе отсчёта (лоренцево сокращение), а ход движущихся часов замедляется, если наблюдать их из «неподвижной» системы отсчёта (релятивистское замедление времени).