
- •21. Резонанс.
- •22. Уравнение плоской синусоидальной волны
- •Вопрос 23
- •Основные соотношения
- •Вопрос 24
- •Вид уравнения
- •Вопрос 25
- •Вопрос 26
- •Частные случаи
- •Вопрос 27
- •Вопрос 28
- •Разность потенциалов
- •Магнитное поле кругового тока — Создается током текущему по тонкому круглому проводу
- •Закон Ампера — Если провод, по которому течет ток, находится в магнитном поле, то на каждый из носителей тока действует сила Ампера
- •61 Вопрос.
- •62 Вопрос.
- •63 Вопрос
- •Второй закон излучения Вина
- •82. Энергия и импульс фотона.
- •83. Эффект Комптона. Корпускулярно-волновая двойственность свойвств света.
- •84. Корпускулярно-волновой дуализм свойств материи. Гипотеза де Бройля. Дифракция электронов. Соотношения неопределенностей. Набор одновременно измеримых величин.
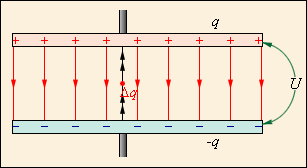
Разность потенциалов
![]()
![]()
Напряжение — разность значений потенциала в начальной и конечной точках траектории.
Напряжение численно равно работе электростатического поля при перемещении единичного положительного заряда вдоль силовых линий этого поля.
Разность потенциалов (напряжение) не зависит от выбора системы координат!
45. Связь напряженности с потенциалом.
Из
доказанного выше:
![]() Þ
Þ
![]()
напряженность равна градиенту потенциала (скорости изменения потенциала вдоль направления d).

Из этого соотношения видно:
1. Вектор напряженности направлен в сторону уменьшения потенциала.
2. Электрическое поле существует, если существует разность потенциалов.
3.
Единица напряженности:
![]() - Напряженность
поля равна
- Напряженность
поля равна
1 В/м, если между двумя точками поля, находящимися на расстоянии 1 м друг от друга существует разность потенциалов 1 В.

![]()
46. Электрическое поле в диэлектриках и проводниках
электрическое поле может существовать не только в вакууме, но и внутри вещества, ибо электрические силы могут действовать и внутри различных тел. При этом, однако, надо иметь в виду существенное различие между проводниками и диэлектриками. В проводнике имеются электрические заряды, свободно перемещающиеся под действием электрических сил. В диэлектрике же движение зарядов под действием электрических сил происходить не может. Поэтому, если в проводнике возникло электрическое поле, то свободные заряды проводника придут в движение под действием этого поля, т. е. через проводник будет идти электрический ток. Равновесие будет достигнуто, когда заряды распределятся по проводнику таким образом, чтобы создаваемое ими внутри проводника электрическое поле как раз компенсировало внешнее поле, вызвавшее перемещение зарядов. Пока такая компенсация не наступила, электрические заряды, благодаря их подвижности в проводнике, будут продолжать движение. Таким образом, при равновесии зарядов напряженность электрического поля в проводнике равна нулю, т. е. электрическое поле в проводнике отсутствует. В диэлектрике наличие электрического поля не препятствует равновесию зарядов. Сила, действующая на заряды в диэлектрике со стороны электрического поля, уравновешивается внутримолекулярными силами, удерживающими заряды в пределах молекулы диэлектрика, так что в диэлектрике возможно равновесие зарядов, несмотря на наличие электрического поля. разделение тел на проводники и диэлектрики условно. При достаточно большой напряженности поля и в диэлектрике возможно заметное перемещение зарядов, ведущее к пробою диэлектрика. Однако при общепринятом разделении тел на проводники и диэлектрики мы можем сказать, что в случае равновесия зарядов электрическое поле внутри проводника (например, металла) отсутствует, а электрическое поле в диэлектрике (например, в стекле) может существовать.
47. Теорема Остроградского-Гаусса. Поток вектора напряженности электрического поля.
Чтобы продвинуться дальше в изучении
электрического поля, необходимо
использовать векторный анализ -
математический аппарат. Мы должны знать,
что такое градиент, ротор, дивиргенция.
Начнем же с понятия " поток вектора
![]() "
.
"
.
П усть
имеем однородное электрическое поле
(напряженность которого одинакова во
всех точках пространства) с напряженностью
,
которое пронизывает некоторую плоскую
поверхность площади S, тогда скаляр-
усть
имеем однородное электрическое поле
(напряженность которого одинакова во
всех точках пространства) с напряженностью
,
которое пронизывает некоторую плоскую
поверхность площади S, тогда скаляр-
ное произведение
![]() будет
называться потоком вектора напряженности
через
поверхность S, (см. рис. 1), т.е.
будет
называться потоком вектора напряженности
через
поверхность S, (см. рис. 1), т.е.
![]() ,
(1)
,
(1)
где
![]() -
есть вектор, равный произведению величины
площади на нормаль к этой поверхности,
Еn -проекция вектора
на
нормаль,
-
есть вектор, равный произведению величины
площади на нормаль к этой поверхности,
Еn -проекция вектора
на
нормаль,
![]() к
площадке.
к
площадке.
В общем случае поле может быть неоднородным,
поверхность неплоской. В этом случае
поверхность можно мысленно разбить на
бесконечно малые элементарные площадки
dS, которые можно считать плоскими, а
поле вблизи них однородным. В таком
случае поток через элементарную площадку
![]() .
(2)
.
(2)
Полный поток вектора напряженности через поверхность S
![]() .
(3)
.
(3)
Н айдем
поток вектора напряженности электрического
поля, создаваемого точечным зарядом q,
через сферическую поверхность радиуса
r.
айдем
поток вектора напряженности электрического
поля, создаваемого точечным зарядом q,
через сферическую поверхность радиуса
r.
Площадь ее поверхности![]() .
Силовые линии электрического поля, (см.
рис. 2), идут по радиусам к поверхности
сферы и поэтому угол между векторами
и
равен
нулю.
.
Силовые линии электрического поля, (см.
рис. 2), идут по радиусам к поверхности
сферы и поэтому угол между векторами
и
равен
нулю.
 .
(4)
.
(4)
Можно показать, что поток через замкнутую поверхность не зависит от формы поверхности и от расположения зарядов в ней.
Рассмотрим поток, создаваемый системой
зарядов, сквозь замкнутую поверхность
произвольной формы, внутри которой они
находятся (рис.3):
![]() .
.
48. Применение теоремы Остроградского-Гаусса для определения напряженности электрического поля.
Применение теоремы Гаусса
Являясь (вкупе с уравнением о нулевой циркуляции электрического поля) основным полевым уравнением электростатики (вместе эти два уравнения в дифференциальной форме эквивалентны уравнению Пуассона — основному и единственному дифференциальному уравнению классической теории для электростатического потенциала.
В электродинамике теорема Гаусса (закон Гаусса) также остается (полностью в том же виде) одним из главных уравнений — одним из четырех уравнений Максвелла.
В некоторых ситуациях теорема Гаусса может быть использована для прямого и легкого вычисления электростатического поля непосредственно. Это ситуации, когда симметрия задачи позволяет наложить на напряженность электрического поля такие дополнительные условия, что вместе с теоремой Гаусса этого хватает для прямого элементарного вычисления (без применения двух обычных общих способов — решения уравнения в частных производных или лобового интегрирования кулоновских полей для элементарных точечных зарядов).
Именно таким способом с использованием теоремы Гаусса может быть выведен и сам закон Кулона (см. выше).
Конкретные примеры такого применения теоремы Гаусса разобраны здесь ниже.
В них используются следующие величины и обозначения:
Объёмная плотность заряда
![]()
где
![]() —
(бесконечно малый) элемент объема,
—
(бесконечно малый) элемент объема,
Поверхностная плотность заряда
![]()
где
![]() —
(бесконечно малый) элемент поверхности.
—
(бесконечно малый) элемент поверхности.
Линейная плотность заряда
![]()
где
![]() —
длина бесконечно малого отрезка. (Первая
используется для зарядов, непрерывно
распределенных по объему, вторая —
для распределенных по поверхности,
третья — для распределенных по
одномерной линии (кривой, прямой).
—
длина бесконечно малого отрезка. (Первая
используется для зарядов, непрерывно
распределенных по объему, вторая —
для распределенных по поверхности,
третья — для распределенных по
одномерной линии (кривой, прямой).
Расчет напряженности поля сферически симметричного распределения заряда
Способ расчета с помощью теоремы Гаусса для любого сферически симметричного распределения заряда в целом сводится к тому, что описано выше для случая точечного заряда (см. параграф о законе Кулона).
Отметим тут только в отношении неточечных источников обладающих сферической симметрией вот что (всё это является очевидными следствиями применения описанного там метода):
Сферически симметричный заряд с концентрической сферической пустотой (или незаряженной областью) в середине, не создает внутри этой пустоты поля (напряженность поля там равна нулю).
Вообще поле на расстоянии r от центра создается только теми зарядами, которые находятся глубже к центру. Это поле можно рассчитать по закону Кулона:
 ,
только под Q
здесь следует понимать суммарный заряд
шаровой области радиусом r
(а это означает, что зависимость от r
в итоге отличается от кулоновской,
поскольку с ростом r
растет Q,
по карйней мере пока r
не больше радиуса всей заряженной
области — если только она в свою
очередь конечна).
,
только под Q
здесь следует понимать суммарный заряд
шаровой области радиусом r
(а это означает, что зависимость от r
в итоге отличается от кулоновской,
поскольку с ростом r
растет Q,
по карйней мере пока r
не больше радиуса всей заряженной
области — если только она в свою
очередь конечна).При r, больших радиуса заряженной области (если он конечен), выполняется самый обычный закон Кулона (как для точечного заряда). Это объясняет, например, почему обычный закон Кулона работает для равномерно заряженных шаров, сфер, планет со структурой близкой к сферически симметричной даже вблизи их поверхности (например, почему вблизи поверхности Земли гравитационное поле достаточно близко к полю точечной массы, сосредоточенной в центре Земли).
В интересном частном случае равномерно заряженного шара, его электрическое (или гравитационное) поле оказывается внутри шара пропорциональным расстоянию до центра.[21]
Расчёт напряжённости поля бесконечной плоскости

![]()
Рассмотрим
поле, создаваемое бесконечной однородно
заряженной плоскостью с везде одинаковой
поверхностной плотностью заряда
![]() .
Представим себе мысленно цилиндр с
образующими, перпендикулярными к
заряженной плоскости, и основаниями
(площадью
.
Представим себе мысленно цилиндр с
образующими, перпендикулярными к
заряженной плоскости, и основаниями
(площадью
![]() каждое),
расположенными относительно плоскости
симметрично (см. рисунок).
каждое),
расположенными относительно плоскости
симметрично (см. рисунок).
В силу симметрии:
Все векторы напряжённости поля (в том числе
 и
и
 ) —
перпендикулярны заряженной плоскости:
действительно, в силу вращательной
симметрии задачи, вектор напряжённости
при любом повороте относительно оси,
перпендикулярной плоскости, должен
переходить в себя, а это возможно для
ненулевого вектора только если он
перпендикулярен плоскости. Из этого
следует (кроме прочего), что поток
напряжённости поля через боковую
поверхность цилиндра равен нулю (так
как поле направлено везде по касательной
к этой поверхности).
) —
перпендикулярны заряженной плоскости:
действительно, в силу вращательной
симметрии задачи, вектор напряжённости
при любом повороте относительно оси,
перпендикулярной плоскости, должен
переходить в себя, а это возможно для
ненулевого вектора только если он
перпендикулярен плоскости. Из этого
следует (кроме прочего), что поток
напряжённости поля через боковую
поверхность цилиндра равен нулю (так
как поле направлено везде по касательной
к этой поверхности). .
.
Поток
вектора напряжённости равен (в силу
(1)) потоку только через основания
цилиндра, а он, в силу того, что
и
перпендикулярны
этим основаниям и в силу (2), равен просто
![]() .
.
Применив
теорему Гаусса, и учитывая
![]() ,
получим (в системе СИ):
,
получим (в системе СИ):
![]()
из чего
![]()
В системе СГСЭ все рассуждения полностью аналогичны (с точностью до постоянных коэффициентов), а ответ записывается как

Расчёт напряжённости поля бесконечной нити

Рассмотрим
поле, создаваемое бесконечной прямолинейной
нитью с линейной плотностью заряда,
равной
.
Пусть требуется определить напряжённость,
создаваемую этим полем на расстоянии
от
нити. Возьмём в качестве гауссовой
поверхности цилиндр с осью, совпадающей
с нитью, радиусом
и
высотой
![]() .
Тогда поток напряжённости через эту
поверхность по теореме Гаусса таков (в
единицах СИ):
.
Тогда поток напряжённости через эту
поверхность по теореме Гаусса таков (в
единицах СИ):
![]()
В силу симметрии
вектор напряженности поля направлен перпендикулярно нити, прямо от нее (или прямо к ней).
модуль этого вектора в любой точке поверхности цилиндра одинаков.
Тогда поток напряжённости через эту поверхность можно рассчитать следующим образом:
![]()
Учитывается
только площадь боковой поверхности
цилиндра, так как поток через основания
цилиндра равен нулю (вследствие
направления E
по касательной к ним). Приравнивая два
полученных выражения для
![]() ,
имеем:
,
имеем:
![]()
![]()
(В
системе СГС
ответ:
![]() ).
).
49. Электрическая емкость уединенного проводника. Конденсаторы. Емкость плоского конденсатора
Электроемкость уединенного проводника.
Электроемкость уединенного проводника - это физическая величина, численно равная заряду, необходимoму для повышения потенциала проводника на 1 В:
![]()
Найдем емкость проводника формой шара радиуса R:

Найдем размер шара емкостью 1Ф:
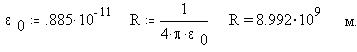
При этом емкость шара размером в земной равна:
![]()
Избыточный заряд величиной 1 Кл поднял бы потенциал такого шара на
![]()
Как видим, емкость проводника определена его "габаритами". Совершенно аналогично, "энергетическая емкость" бочки, т. е. величина, численно равная массе воды, необходимой для повышения ее потенциала в поле тяжести на единицу (в однородном поле тяжести на высоте h потенциал численно равен потенциальной энергии 1 кг: gh), прямопропорциональна площади дна бочки.
Диэлектрик в e раз ослабляет поле и,
следовательно, в
![]() раз
увеличивает емкость.
раз
увеличивает емкость.
Электроемкость плоского конденсатора.
Так как знак потенциала точечного заряда совпадает со знаком самого заряда, то индуцирование в близлежащих телах зарядов противоположного знака приводит к уменьшению потенциала "индуцирующего" заряда, что, соответственно, означает увеличение электроемкости системы близлежащих тел, получившей название конденсатор.
Плоский конденсатор представляет из себя две плоские пластины, расстояние между которыми d мало по сравнению с их линейными размерами. Это предположение позволяет пренебречь малыми областями неоднородности электрического поля у краев пластин и считать, что все поле однородно и сосредоточено между пластинами. Заряд конденсатора Q - это заряд положительно заряженной пластины.
Емкость конденсатора определяется как величина, численно равная заряду, необходимому для изменения разности потенциалов пластин, напряжения U между обкладками, на 1 В:
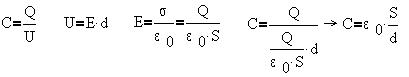
Заполнение пространства между пластинами диэлектриком, очевидно, увеличит емкость в раз.
Конденса́тор (от лат. condensare — «уплотнять», «сгущать») — двухполюсник с определённым значением ёмкости и малой омической проводимостью; устройство для накопления заряда и энергии электрического поля. Конденсатор является пассивным электронным компонентом. Обычно состоит из двух электродов в форме пластин (называемых обкладками), разделённых диэлектриком, толщина которого мала по сравнению с размерами обкладок.
50) Если двум изолированным друг от друга проводникам сообщить заряды q1 и q2, то между ними возникает некоторая разность потенциалов Δφ, зависящая от величин зарядов и геометрии проводников. Разность потенциалов Δφ между двумя точками в электрическом поле часто называют напряжением и обозначают буквой U.
|
|
Таким образом, при параллельном соединении электроемкости складываются.
|
|
При последовательном
соединении (рис. 4.6.4) одинаковыми
оказываются заряды обоих конденсаторов:
q1 = q2 = q, а напряжения на них
равны
![]() и
и
![]() Такую
систему можно рассматривать как единый
конденсатор, заряженный зарядом q при
напряжении между обкладками U = U1 + U2.
Следовательно,
Такую
систему можно рассматривать как единый
конденсатор, заряженный зарядом q при
напряжении между обкладками U = U1 + U2.
Следовательно,
|
|
|
Рисунок 4.7.1. Процесс зарядки конденсатора. |
|
Электрическую энергию We следует рассматривать как потенциальную энергию, запасенную в заряженном конденсаторе. Формулы для We аналогичны формулам для потенциальной энергии Ep деформированной пружины (см. § 2.4)
|
где k – жесткость
пружины, x – деформация, F = kx –
внешняя сила. По современным
представлениям, электрическая энергия
конденсатора локализована в пространстве
между обкладками конденсатора, то есть
в электрическом поле. Поэтому ее называют
энергией электрического поля. Это легко
проиллюстрировать на примере заряженного
плоского конденсатора. Напряженность
однородного поля в плоском конденсаторе
равна E = U/d, а его емкость

|
где V = Sd – объем пространства между обкладками, занятый электрическим полем. Из этого соотношения следует, что физическая величина
|
является электрической (потенциальной) энергией единицы объема пространства, в котором создано электрическое поле. Ее называют объемной плотностью электрической энергии. Энергия поля, созданного любым распределением электрических зарядов в пространстве, может быть найдена путем интегрирования объемной плотности we по всему объему, в котором создано электрическое поле.
51) Если изолированный
проводник поместить в электрическое
поле
![]() то
на свободные заряды q в проводнике будет
действовать сила
то
на свободные заряды q в проводнике будет
действовать сила
![]() В
результате в проводнике возникает
кратковременное перемещение свободных
зарядов. Этот процесс закончится тогда,
когда собственное электрическое поле
зарядов, возникших на поверхности
проводника, не скомпенсирует полностью
внешнее поле. Результирующее
электростатическое поле внутри проводника
равно нулю (см. § 4.5). Однако, в
проводниках может при определенных
условиях возникнуть непрерывное
упорядоченное движение свободных
носителей электрического заряда.
В
результате в проводнике возникает
кратковременное перемещение свободных
зарядов. Этот процесс закончится тогда,
когда собственное электрическое поле
зарядов, возникших на поверхности
проводника, не скомпенсирует полностью
внешнее поле. Результирующее
электростатическое поле внутри проводника
равно нулю (см. § 4.5). Однако, в
проводниках может при определенных
условиях возникнуть непрерывное
упорядоченное движение свободных
носителей электрического заряда.
|
Если сила тока и его направление не изменяются со временем, то такой ток называется постоянным.
Постоянный
электрический ток может быть создан
только в замкнутой цепи, в которой
свободные носители заряда циркулируют
по замкнутым траекториям. Электрическое
поле в разных точках такой цепи неизменно
во времени. Следовательно, электрическое
поле в цепи постоянного тока имеет
характер замороженного электростатического
поля. Но при перемещении электрического
заряда в электростатическом поле по
замкнутой траектории, работа электрических
сил равна нулю. Поэтому для существования
постоянного тока необходимо наличие в
электрической цепи устройства, способного
создавать и поддерживать разности
потенциалов на участках цепи за счет
работы сил неэлектростатического
происхождения. Такие устройства
называются источниками
постоянного тока.
Силы неэлектростатического происхождения,
действующие на свободные носители
заряда со стороны источников тока,
называются сторонними
силами.
Природа сторонних сил может быть
различной. В гальванических элементах
или аккумуляторах они возникают в
результате электрохимических процессов,
в генераторах постоянного тока сторонние
силы возникают при движении проводников
в магнитном поле. Источник тока в
электрической цепи играет ту же роль,
что и насос, который необходим для
перекачки жидкости в замкнутой
гидравлической системе. Под действием
сторонних сил электрические заряды
движутся внутри источника тока против
сил электростатического поля, благодаря
чему в замкнутой цепи может поддерживаться
постоянный электрический ток. При
перемещении электрических зарядов по
цепи постоянного тока сторонние силы,
действующие внутри источников тока,
совершают работу. Физическая
величина, равная отношению работы Aст
сторонних сил при перемещении заряда
q от отрицательного полюса источника
тока к положительному к величине этого
заряда, называется электродвижущей
силой источника (ЭДС):
![]() Таким образом, ЭДС определяется работой,
совершаемой сторонними силами при
перемещении единичного положительного
заряда. Электродвижущая сила, как и
разность потенциалов, измеряется в
вольтах
(В). При перемещении единичного
положительного заряда по замкнутой
цепи постоянного тока работа сторонних
сил равна сумме ЭДС, действующих в этой
цепи, а работа электростатического поля
равна нулю. Цепь постоянного тока можно
разбить на определенные участки. Те
участки, на которых не действуют сторонние
силы (то есть участки, не содержащие
источников тока), называются однородными.
Участки, включающие источники тока,
называются неоднородными.
При перемещении единичного положительного
заряда по некоторому участку цепи работу
совершают как электростатические
(кулоновские), так и сторонние силы.
Работа электростатических сил равна
разности потенциалов Δφ12 = φ1 – φ2
между начальной (1) и конечной (2) точками
неоднородного участка. Работа сторонних
сил равна по определению электродвижущей
силе
Таким образом, ЭДС определяется работой,
совершаемой сторонними силами при
перемещении единичного положительного
заряда. Электродвижущая сила, как и
разность потенциалов, измеряется в
вольтах
(В). При перемещении единичного
положительного заряда по замкнутой
цепи постоянного тока работа сторонних
сил равна сумме ЭДС, действующих в этой
цепи, а работа электростатического поля
равна нулю. Цепь постоянного тока можно
разбить на определенные участки. Те
участки, на которых не действуют сторонние
силы (то есть участки, не содержащие
источников тока), называются однородными.
Участки, включающие источники тока,
называются неоднородными.
При перемещении единичного положительного
заряда по некоторому участку цепи работу
совершают как электростатические
(кулоновские), так и сторонние силы.
Работа электростатических сил равна
разности потенциалов Δφ12 = φ1 – φ2
между начальной (1) и конечной (2) точками
неоднородного участка. Работа сторонних
сил равна по определению электродвижущей
силе
![]() 12,
действующей на данном участке. Поэтому
полная работа равна
12,
действующей на данном участке. Поэтому
полная работа равна
U12 = φ1 – φ2 +
12. |
U12 = φ1 – φ2. |
|
|
Это соотношение принято называть обобщенным законом Ома. По закону Ома,
IR = Δφcd. |
Участок (ab) содержит источник тока с ЭДС, равной . По закону Ома для неоднородного участка,
Ir = Δφab + . |
Сложив оба равенства, получим:
I(R + r) = Δφcd + Δφab + . |
|
Эта формула выражет закон Ома для полной цепи: сила тока в полной цепи равна электродвижущей силе источника, деленной на сумму сопротивлений однородного и неоднородного участков цепи. Сопротивление r неоднородного участка на рис. 4.8.2 можно рассматривать как внутреннее сопротивление источника тока. В этом случае участок (ab) на рис. 4.8.2 является внутренним участком источника. Если точки a и b замкнуть проводником, сопротивление которого мало по сравнению с внутренним сопротивлением источника (R << r), тогда в цепи потечет ток короткого замыкания
|
Сила тока короткого замыкания – максимальная сила тока, которую можно получить от данного источника с электродвижущей силой и внутренним сопротивлением r. У источников с малым внутренним сопротивлением ток короткого замыкания может быть очень велик и вызывать разрушение электрической цепи или источника. Например, у свинцовых аккумуляторов, используемых в автомобилях, сила тока короткого замыкания может составлять несколько сотен ампер. Особенно опасны короткие замыкания в осветительных сетях, питаемых от подстанций (тысячи ампер). Чтобы избежать разрушительного действия таких больших токов, в цепь включаются предохранители или специальные автоматы защиты сетей. В ряде случаев для предотвращения опасных значений силы тока короткого замыкания к источнику подсоединяется некоторое внешнее балластное сопротивление. Тогда сопротивление r равно сумме внутреннего сопротивления источника и внешнего балластного сопротивления. Если внешняя цепь разомкнута, то Δφba = – Δφab = , то есть разность потенциалов на полюсах разомкнутой батареи равна ее ЭДС. Если внешнее нагрузочное сопротивление R включено и через батарею протекает ток I, разность потенциалов на ее полюсах становится равной
Δφba = – Ir. |
На рис. 4.8.3
дано схематическое изображение источника
постоянного тока с ЭДС равной
и
внутренним сопротивлением r в трех
режимах: «холостой ход», работа на
нагрузку и режим короткого замыкания
(к. з.). Указаны напряженность
![]() электрического
поля внутри батареи и силы, действующие
на положительные заряды:
электрического
поля внутри батареи и силы, действующие
на положительные заряды:
![]() –
электрическая сила и
–
электрическая сила и
![]() –
сторонняя сила. В режиме короткого
замыкания электрическое поле внутри
батареи исчезает.
–
сторонняя сила. В режиме короткого
замыкания электрическое поле внутри
батареи исчезает.
Для измерения напряжений и токов в электрических цепях постоянного тока используются специальные приборы – вольтметры и амперметры. Вольтметр предназначен для измерения разности потенциалов, приложенной к его клеммам. Он подключается параллельно участку цепи, на котором производится измерение разности потенциалов. Любой вольтметр обладает некоторым внутренним сопротивлением RB. Для того, чтобы вольтметр не вносил заметного перераспределения токов при подключении к измеряемой цепи, его внутреннее сопротивление должно быть велико по сравнению с сопротивлением того участка цепи, к которому он подключен. Для цепи, изображенной на рис. 4.8.4, это условие записывается в виде:
RB >> R1. |
Это условие означает, что ток IB = Δφcd / RB, протекающий через вольтметр, много меньше тока I = Δφcd / R1, который протекает по узмеряемому участку цепи. Поскольку внутри вольтметра не действуют сторонние силы, разность потенциалов на его клеммах совпадает по определению с напряжением. Поэтому можно говорить, что вольтметр измеряет напряжение. Амперметр предназначен для измерения силы тока в цепи. Амперметр включается последовательно в разрыв электрической цепи, чтобы через него проходил весь измеряемый ток. Амперметр также обладает некоторым внутренним сопротивлением RA. В отличие от вольтметра, внутреннее сопротивление амперметра должно быть достаточно малым по сравнению с полным сопротивлением всей цепи. Для цепи на рис. 4.8.4 сопротивление амперметра должно удовлетворять условию
RA << (r – R1 + R2), |
чтобы при включении амперметра ток в цепи не изменялся. Измерительные приборы – вольтметры и амперметры – бывают двух видов: стрелочные (аналоговые) и цифровые. Цифровые электроизмерительные приборы представляют собой сложные электронные устройства. Обычно цифровые приборы обеспечивают более высокую точность измерений.
53,54) При протекании тока по однородному участку цепи электрическое поле совершает работу. За время Δt по цепи протекает заряд Δq = IΔt. Электрическое поле на выделенном учестке совершает работу
ΔA = (φ1 – φ2)Δq = Δφ12IΔt = UIΔt, |
где U = Δφ12 – напряжение. Эту работу называют работой электрического тока. Если обе части формулы
RI = U, |
выражающей закон Ома для однородного участка цепи с сопротивлением R, умножить на IΔt, то получится соотношение
RI2Δt = UIΔt = ΔA. |
Это соотношение выражает закон сохранения энергии для однородного участка цепи. Работа ΔA электрического тока I, протекающего по неподвижному проводнику с сопротивлением R, преобразуется в тепло ΔQ, выделяющееся на проводнике.
|
Закон преобразования работы тока в тепло был экспериментально установлен независимо друг от друга Дж. Джоулем и Э. Ленцем и носит название закона Джоуля–Ленца. Мощность электрического тока равна отношению работы тока ΔA к интервалу времени Δt, за которое эта работа была совершена:
|
Работа электрического тока в СИ выражается в джоулях (Дж), мощность – в ваттах (Вт). Рассмотрим теперь полную цепь постоянного тока, состоящую из источника с электродвижущей силой и внутренним сопротивлением r и внешнего однородного участка с сопротивлением R. Закон Ома для полной цепи записывается в виде
(R + r)I = . |
Умножив обе части этой формулы на Δq = IΔt, мы получим соотношение, выражающее закон сохранения энергии для полной цепи постоянного тока:
RI2Δt + rI2Δt = IΔt = ΔAст. |
Первый член в левой части ΔQ = RI2Δt – тепло, выделяющееся на внешнем участке цепи за время Δt, второй член ΔQист = rI2Δt – тепло, выделяющееся внутри источника за то же время. Выражение IΔt равно работе сторонних сил ΔAст, действующих внутри источника. При протекании электрического тока по замкнутой цепи работа сторонних сил ΔAст преобразуется в тепло, выделяющееся во внешней цепи (ΔQ) и внутри источника (ΔQист).
. |
Следует обратить внимание, что в это соотношение не входит работа электрического поля. При протекании тока по замкнутой цепи электрическое поле работы не совершает; поэтому тепло производится одними только сторонними силами, действующими внутри источника. Роль электрического поля сводится к перераспределению тепла между различными участками цепи. Внешняя цепь может представлять собой не только проводник с сопротивлением R, но и какое-либо устройство, потребляющее мощность, например, электродвигатель постоянного тока. В этом случае под R нужно понимать эквивалентное сопротивление нагрузки. Энергия, выделяемая во внешней цепи, может частично или полностью преобразовываться не только в тепло, на и в другие виды энергии, например, в механическую работу, совершаемую электродвигателем. Поэтому вопрос об использовании энергии источника тока имеет большое практическое значение. Полная мощность источника, то есть работа, совершаемая сторонними силами за единицу времени, равна
|
Во внешней цепи выделяется мощность
|
|
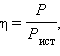 равное
равноеназывается коэффициентом полезного действия источника.
55) Для упрощения расчетов сложных электрических цепей, содержащих неоднородные участки, используются правила Кирхгофа, которые являются обобщением закона Ома на случай разветвленных цепей. В разветвленных цепях можно выделить узловые точки (узлы), в которых сходятся не менее трех проводников (рис. 4.10.1). Токи, втекающие в узел, принято считать положительными; токи, вытекающие из узла – отрицательными.
|
Рисунок 4.10.1. Узел электрической цепи. I1, I2 > 0; I3, I4 < 0 |
В узлах цепи постоянного тока не может происходить накопление зарядов. Отсюда следует первое правило Кирхгофа: Алгебраическая сумма сил токов для каждого узла в разветвленной цепи равна нулю:
|
Первое правило Кирхгофа является следствием закона сохранения электрического заряда. В разветвленной цепи всегда можно выделить некоторое количество замкнутых путей, состоящих из однородных и неоднородных участков. Такие замкнутые пути называются контурами. На разных участках выделенного контура могут протекать различные токи. На рис. 4.10.2 представлен простой пример разветвленной цепи. Цепь содержит два узла a и d, в которых сходятся одинаковые токи; поэтому только один из узлов является независимым (a или d).
|
Рисунок 4.10.2. Пример разветвленной электрической цепи. Цепь содержит один независимый узел (a или d) и два независимых контура (например, abcd и adef). |
В цепи можно выделить три контура abcd, adef и abcdef. Из них только два являются независимыми (например, abcd и adef), так как третий не содержит никаких новых участков. Второе правило Кирхгофа является следствием обобщенного закона Ома. Запишем обобщенный закон Ома для участков, составляющих один из контуров цепи, изображенной на рис. 4.10.2, например, abcd. Для этого на каждом участке нужно задать положительное направление тока и положительное направление обхода контура. При записи обобщенного закона Ома для каждого из участков необходимо соблюдать определенные «правила знаков», которые поясняются на рис. 4.10.3.
|
Рисунок 4.10.3. «Правила знаков». |
Для участков контура abcd обобщенный закон Ома записывается в виде: Для участка bc: I1R1 = Δφbc – 1. Для участка da: I2R2 = Δφda – 2. Складывая левые и правые части этих равенств и принимая во внимание, что Δφbc = – Δφda , получим:
I1R1 + I2R2 = Δφbc + Δφda – 1 + 2 = – 1 – 2. |
Аналогично, для контура adef можно записать:
– I2R2 + I3R3 = 2 + 3. |
Второе правило Кирхгофа можно сформулировать так: алгебраическая сумма произведений сопротивления каждого из участков любого замкнутого контура разветвленной цепи постоянного тока на силу тока на этом участке равна алгебраической сумме ЭДС вдоль этого контура. Первое и второе правила Кирхгофа, записанные для всех независимых узлов и контуров разветвленной цепи, дают в совокупности необходимое и достаточное число алгебраических уравнений для расчета электрической цепи. Для цепи, изображенной на рис. 4.10.2, система уравнений для определения трех неизвестных токов I1, I2 и I3 имеет вид:
I1R1 + I2R2 = – 1 – 2, |
– I2R2 + I3R3 = 2 + 3, |
– I1 + I2 + I3 = 0. |
56) Магнитное поле представляет собой особую форму материи и проявляется в пространстве в виде определенного рода сил, которые легко обнаруживаются по своему действию на намагниченные тела. Действие этих сил на намагниченные тела объясняется наличием в телах быстро движущихся внутримолекулярных электрических зарядов.
Согласно определению, магнитная индукция и магнитный поток связаны соотношением
![]()
Для характеристики намагниченности вещества в магнитном поле используется магнитный момент рm, который численно равен механическому моменту, испытываемому веществом в магнитном поле с индукцией в 1 Тл
Магнитный момент можно определить из уравнения
![]() где
М - механический момент, испытываемый
веществом; α - угол между вектором
индукции и вектором магнитного момента.
Магнитный момент единицы объема
вещества определяет интенсивность его
намагничивания или намагниченность I
где
М - механический момент, испытываемый
веществом; α - угол между вектором
индукции и вектором магнитного момента.
Магнитный момент единицы объема
вещества определяет интенсивность его
намагничивания или намагниченность I
![]() где
V - объем вещества.
где
V - объем вещества.
Магнитное поле характеризуется напряженностью H. Напряженностью магнитного поля в данной точке называется сила, с которой поле действует на единицу положительной магнитной массы, помещенную в эту точку поля.
![]()
Магнитная индукция В связана с напряженностью магнитного поля соотношением
![]()
где μ - относительная магнитная проницаемость среды; μ0 - магнитная постоянная.
Неоднородность магнитного поля в данной его точке характеризуется градиентом его напряженности grad H:
![]()
Для однородных полей dH/dx=0, для неоднородных dH/dx>0. Силой магнитного поля Fп(А2/м3) в данной его точке называют произведение градиента его напряженности на напряженность поля в данной точке
![]()
Магнитные свойства вещества характеризуются магнитной восприимчивостью х и удельной магнитной восприимчивостью
![]() где
δ - плотность вещества.
где
δ - плотность вещества.
Магнитная сила
![]() м,
действующая на минеральное зерно с
массой т, помещенное в магнитное поле,
оценивается зависимостью
м,
действующая на минеральное зерно с
массой т, помещенное в магнитное поле,
оценивается зависимостью
![]() где
удельная магнитная сила
где
удельная магнитная сила
![]() Одно
из важнейших свойств магнитного поля
- явление электромагнитной индукции.
Его суть состоит в том, что при всяком
изменении магнитного потока, пронизывающего
какой-либо контур, в нем наводится
электродвижущая сила. Другим свойством
магнитного поля является механическое
взаимодействие его с электрическим
током. Минеральные частицы, попадая в
магнитное поле, влияют на расположение
его силовых линий. Магнитные частицы
оказывают небольшое сопротивление
магнитным силовым линиям, поэтому
последние в них концентрируются.
Устремляясь по кратчайшему пути, силовые
линии втягивают магнитные частицы в
пространство между полюсами. Немагнитные
частицы ухудшают проводимость, поэтому
силовые линии обходят их и выталкивают
из поля. Магнитная
индукция – векторная физическая
величина, численно равная силе, с которой
магнитное поле действует на единицу
длины прямолинейного проводника с
током, равным единице силы тока,
расположенном перпендикулярно направлению
поля.
Одно
из важнейших свойств магнитного поля
- явление электромагнитной индукции.
Его суть состоит в том, что при всяком
изменении магнитного потока, пронизывающего
какой-либо контур, в нем наводится
электродвижущая сила. Другим свойством
магнитного поля является механическое
взаимодействие его с электрическим
током. Минеральные частицы, попадая в
магнитное поле, влияют на расположение
его силовых линий. Магнитные частицы
оказывают небольшое сопротивление
магнитным силовым линиям, поэтому
последние в них концентрируются.
Устремляясь по кратчайшему пути, силовые
линии втягивают магнитные частицы в
пространство между полюсами. Немагнитные
частицы ухудшают проводимость, поэтому
силовые линии обходят их и выталкивают
из поля. Магнитная
индукция – векторная физическая
величина, численно равная силе, с которой
магнитное поле действует на единицу
длины прямолинейного проводника с
током, равным единице силы тока,
расположенном перпендикулярно направлению
поля.
За единицу магнитной индукции в системе СИ принята тесла (Т), равная индукции однородного магнитного поля, действующего с силой 1 Н на каждый метр длины прямолинейного проводника с током 1 А, если проводник расположен перпендикулярно направлению поля. Размерность единицы магнитной индукции
[Т] = [Н]/[А]·[м] = кг · с-2 · А-1.
Вектор В направлен в каждой точке линии магнитной индукции по касательной к ней. Индукция В характеризует силовое действие магнитного поля на ток. Аналогичную роль играет напряженность Е электростатического поля, характеризующая его силовое действие на заряд.
56.
Магнитное поле и его характеристики. При прохождении электрического тока по проводнику вокруг него образуется магнитное поле. Магнитное поле представляет собой один из видов материи. Оно обладает энергией, которая проявляет себя в виде электромагнитных сил, действующих на отдельные движущиеся электрические заряды (электроны и ионы) и на их потоки, т. е. электрический ток. Под влиянием электромагнитных сил движущиеся заряженные частицы отклоняются от своего первоначального пути в направлении, перпендикулярном полю (рис. 34). Магнитное поле образуется только вокруг движущихся электрических зарядов, и его действие распространяется тоже лишь на движущиеся заряды. Магнитное и электрические поля неразрывны и образуют совместно единое электромагнитное поле. Всякое изменение электрического поля приводит к появлению магнитного поля и, наоборот, всякое изменение магнитного поля сопровождается возникновением электрического поля.
Магнитная
индукция
![]() —
векторная
величина, являющаяся силовой характеристикой
магнитного
поля (его действия на заряженные
частицы) в данной точке пространства.
Определяет, с какой силой
—
векторная
величина, являющаяся силовой характеристикой
магнитного
поля (его действия на заряженные
частицы) в данной точке пространства.
Определяет, с какой силой
![]() магнитное
поле действует на заряд
магнитное
поле действует на заряд
![]() ,
движущийся со скоростью
,
движущийся со скоростью
![]() .
.
Более
конкретно,
—
это такой вектор, что сила
Лоренца
,
действующая со стороны магнитного поля
на заряд
,
движущийся со скоростью
![]() ,
равна
,
равна
![]()
![]()
Также магнитная индукция может быть определена как отношение максимального механического момента сил, действующих на рамку с током, помещенную в однородное поле, к произведению силы тока в рамке на её площадь.
Является основной фундаментальной характеристикой магнитного поля, аналогичной вектору напряжённости электрического поля.
в системе СИ — в теслах (Тл)
57.
Закон Био́—Савара—Лапла́са — физический закон для определения модуля вектора магнитной индукции в любой точке магнитного поля, порождаемого постоянным электрическим током на некотором рассматриваемом участке. Был установлен экспериментально в 1820 году Био и Саваром. Лаплас проанализировал данное выражение и показал, что с его помощью путём интегрирования, в частности, можно вычислить магнитное поле движущегося точечного заряда, если считать движение одной заряженной частицы током.
Формулировка
Пусть
постоянный ток
![]() течёт по контуру γ, находящемуся в
вакууме,
течёт по контуру γ, находящемуся в
вакууме,
![]() —
точка, в которой ищется поле, тогда
индукция магнитного поля в этой точке
выражается интегралом
—
точка, в которой ищется поле, тогда
индукция магнитного поля в этой точке
выражается интегралом
![]()
Направление
![]() перпендикулярно
перпендикулярно
![]() и
и
![]() ,
то есть перпендикулярно плоскости, в
которой они лежат, и совпадает с
касательной к линии магнитной индукции.
Это направление может быть найдено по
правилу нахождения линий магнитной
индукции (правилу правого винта):
направление вращения головки винта
дает направление
,
если поступательное движение буравчика
соответствует направлению тока в
элементе. Модуль вектора
определяется
выражением
,
то есть перпендикулярно плоскости, в
которой они лежат, и совпадает с
касательной к линии магнитной индукции.
Это направление может быть найдено по
правилу нахождения линий магнитной
индукции (правилу правого винта):
направление вращения головки винта
дает направление
,
если поступательное движение буравчика
соответствует направлению тока в
элементе. Модуль вектора
определяется
выражением
![]()


 1
1
 1
1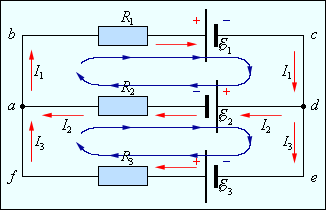 2
2 3
3