4. Описание применяемых методов.

1. Вычисление координат точек при аксонометрическом проецировании.

Инициализация.

• Задаем координаты точки T.

• Задаем координаты камеры, то есть точки C.

• Получаем смещение Cx, Cy центра окна отображения.

• Поворот системы координат на угол ψ вокруг оси X:

Для этого нужно:

1. Рассчитать угол поворота φ вокруг оси X:

Если (a = 0 и b = 0), то cosφ = 1 и sinφ = 0, иначе и .

Результирующая матрица поворота вокруг оси Х:

2. Рассчитать угол поворота ψ вокруг оси:

• Если (a = 0 и b = 0 и c = 0), то cosψ = 1 и sinψ = 0, иначе

и .

Результирующая матрица поворота вокруг оси Х:

3. Проецирование на плоскость xOy:

Результирующая матрица проецирования на плоскость xOy:

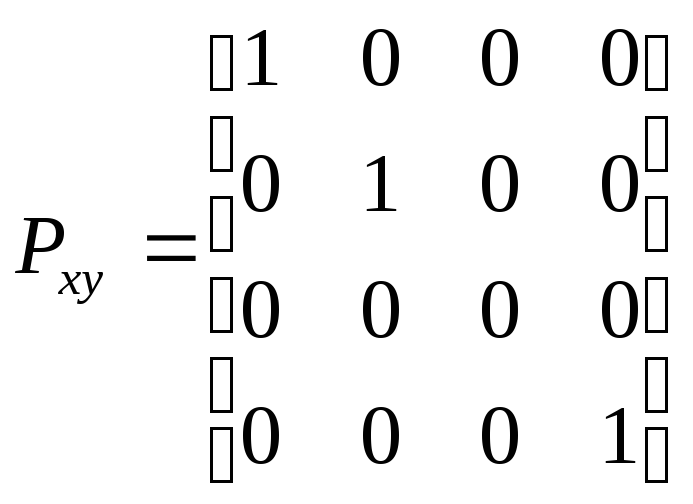
Осуществить операцию умножения координат точки Т и ее проекций на транспонированные матрицы полученные на этапах 1), 2), 3) проецирования.

Приведение координаты точки Т и ее проекций к экранным.

Рассмотрим данную операцию для точки Т (для проекций будет аналогично).

X’ = X + Сx;

Y’ = Y + Сy.

/*Имеются трехмерные координаты точек T, Т1, Т2, Т3, Tx, Ty, Tz, C, xu, xd, yu, yd, zu, zd, где Т1, Т2, Т3, Tx, Ty, Tz – проекции точки Т, С – камера, а остальные точки используются при рисовании осей. Все эти точки мы поместим в массив: Точки типа Точка, который в свою содержит поля для хранения координат.*/

// А – матрица проецирования

//ТочкиВид – этот массив будет содержать результирующие видовые координаты точек.

нач

Матрица.Новая() //«загоняем» в А единичную матрицу

Матрица.Повернуть(Точка C) //Функция состоящая из 2-x последовательных аффинных преобразований, необходимых для поворота к камере

//Преобразуем в новые точки

нц от i:=0 до Точки.Длина

ТочкиВид[i] := Точки[i] * Матрица

кц

кон

На данном этапе мы получаем видовые координаты необходимые для изображения при аксонометрическом преобразовании.

2. Вычисление координат точек при перспективном проецировании.

Чтобы вычислить координаты точек при перспективном преобразовании, нужно взять точки, полученные после преобразования (умножение на матрицу поворота) и провести следующие манипуляции:

1. Высчитываем значение переменной:

2. Далее для каждой точки:

; .

/*Имеются трехмерные координаты точек T, Т1, Т2, Т3, Tx, Ty, Tz, C, xu, xd, yu, yd, zu, zd, где Т1, Т2, Т3, Tx, Ty, Tz – проекции точки Т, С – камера, а остальные точки используются при рисовании осей. Все эти точки мы поместим в массив: Точки типа Точка, который в свою содержит поля для хранения координат.*/

// А – матрица проецирования

//ТочкиВид – этот массив будет содержать результирующие видовые координаты точек.

нач

Матрица.Новая() //«загоняем» в А единичную матрицу

Матрица.Повернуть(Точка C) //Функция состоящая из 2-x последовательных аффинных преобразований, необходимых для поворота к камере

//Преобразуем в новые точки

нц от i:=0 до Точки.Длина

ТочкиВид[i] := Точки[i] * Матрица

кц

d = кореньиз(C.X*С.Х+C.Y*C.Y+C.Z*C.Z)

//Преобразуем в новые точки(перспективные)

нц от i:=0 до ТочкиВид.Длина

если (d-ТочкиВид[i].Z) > 1

нач

ТочкиВид[i].X:=ТочкиВид[i].X*(d/(d-ТочкиВид[i].Z))

ТочкиВид[i].Y:=ТочкиВид[i].Y*(d/(d-ТочкиВид[i].Z))

кон

иначе

нач

ТочкиВид[i].X:=ТочкиВид[i].X*d

ТочкиВид[i].Y:=ТочкиВид[i].Y*d

кон

кц

кон

И вот тут-то мы можем использовать полученные точки для прорисовки. Прорисовка уже освещалась в первой лабораторной работе, стоит добавить лишь проверку на выход элементов чертежа за границу и расположение камеры внутри объекта, выводя соответствующие сообщения:

если (P.x>C.x и P.y>C.y и P.z>C.z)

состояние=камера внутри

если (X<0 или Х>ширина_области или Y<0 или Y>высота_области)

состояние=выход за границы