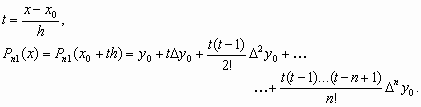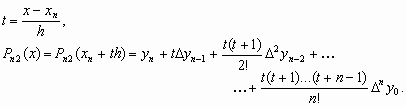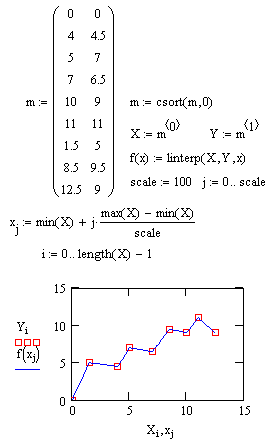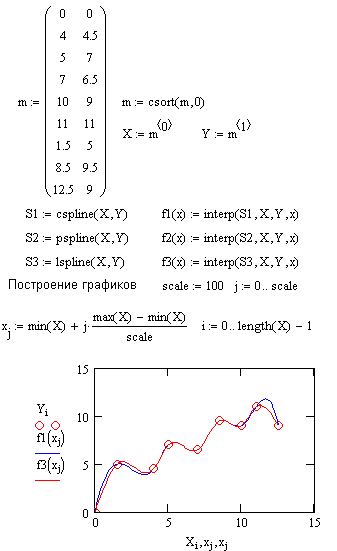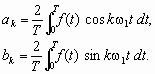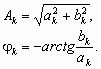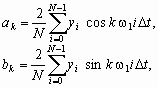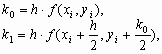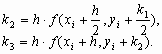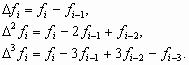Решение систем линейных алгебраических уравнений различными методами.

MathCAD дает возможность решать также и системы уравнений. Максимальное число уравнений и переменных равно 50. Результатом решения системы будет численное значение искомого корня.

Для решения системы уравнений необходимо выполнить следующее:

• Задать начальное приближение для всех неизвестных, входящих в систему уравнений. Mathcad решает систему с помощью итерационных методов.

• Напечатать ключевое слово Given. Оно указывает Mathcad, что далее следует система уравнений.

• Введите уравнения и неравенства в любом порядке. Используйте [Ctrl]= для печати символа =. Между левыми и правыми частями неравенств может стоять любой из символов <, >, 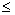  и   .

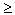• Введите любое выражение, которое включает функцию Find, например: а:= Find(х, у).

Find(z1, z2, . . .)

Возвращает точное решение системы уравнений. Число аргументов должно быть равно числу неизвестных.

Ключевое слово Given, уравнения и неравенства, которые следуют за ним, и какое-либо выражение, содержащее функцию Find, называют блоком решения уравнений.

Следующие выражения недопустимы внутри блока решения:

• Ограничения со знаком   .

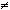• Дискретный аргумент или выражения, содержащие дискретный аргумент в любой форме.

• Неравенства вида a < b < c.

Блоки решения уравнений не могут быть вложены друг в друга, каждый блок может иметь только одно ключевое слово Given и имя функции Find.

Функция, которая завершает блок решения уравнений, может быть использована аналогично любой другой функции. Можно произвести с ней следующие три действия:

• Можно вывести найденное решение, напечатав выражение вида:

Find(var1, var2,…) =.

• Определить переменную с помощью функции Find:

a := Find(x) - скаляр,

var := Find(var1, var2,…) - вектор.

Это удобно сделать, если требуется использовать решение системы уравнений в другом месте рабочего документа.

• Определить другую функцию с помощью Find

f(a, b, c, …) := Find(x, y, z, …).

Эта конструкция удобна для многократного решения системы уравнений для различных значений некоторых параметров a, b, c,…,непосредственно входящих в систему уравнений.

Сообщение об ошибке   (Решение не найдено) при решении уравнений появляется, когда:

• Поставленная задача может не иметь решения.

• Для уравнения, которое не имеет вещественных решений, в качестве начального приближения взято вещественное число и наоборот.

• В процессе поиска решения последовательность приближений попала в точку локального минимума невязки. Для поиска искомого решения нужно задать различные начальные приближения.

• Возможно, поставленная задача не может быть решена с заданной точностью. Попробуйте увеличить значение TOL.

Пример 1 Рисунка 12 иллюстрирует решение системы уравнений в Mathcad.

 

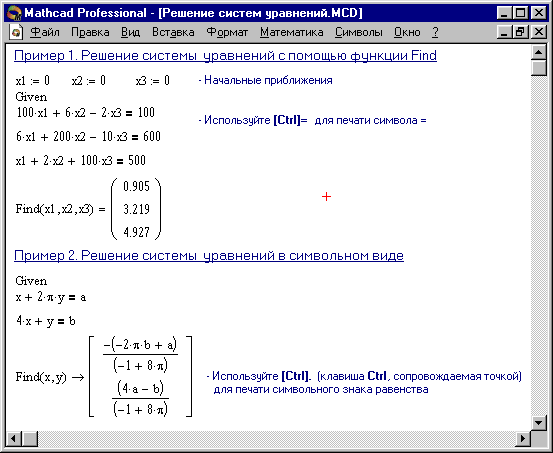
Рисунок 12.

Для решения линейных систем уравнений используется функция lsolve.

Особенности расчета цепей постоянного тока.

Цепь состоит из нескольких ветвей, в каждой из которых находится источник ЭДС и резистор (рис.1). Необходимо рассчитать цепь, то есть определить токи во всех ее ветвях.

Из законов Кирхгофа получаем систему уравнений:

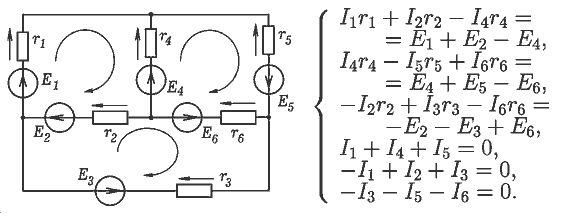
Для решения этой системы уравнений запишем матрицу:

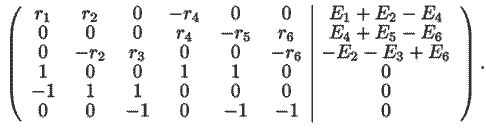
Левую часть матрицы, содержащую коэффициенты при токах I_i, обозначим через A, а правую --- через B. Чтобы получить матрицу токов в MathCAD используется оператор TOK:=A^-1 · B. Решение задачи представлено в документе 03.mcd.

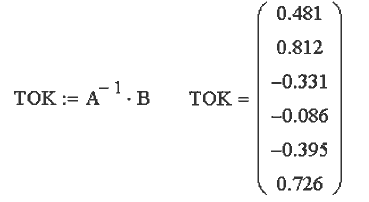
Режимы работы в системе MathCad.

Все примеры неявно предполагают, что включен автоматический режим вычислений. Он включается по умолчанию при создании пустого документа, поэтому если вводятся выражения, содержащие операторы вывода, они вычисляются немедленно. Вообще говоря, имеется два режима вычислений:

автоматический режим (automatic mode) — все вычисления проводятся автоматически по мере ввода формул;

ручной режим (manual mode) — начало вычислений каждой формулы или всего документа производится пользователем.

Режим вычислений можно выбрать с помощью команды Tools / Calculate / Automatic Calculation (Сервис / Пересчитать / Считать автоматически), как показано на рис. 3.14. Если в этой строке меню установлен флажок проверки, значит, включен автоматический режим, если флажка нет, то редактируется документ в ручном режиме вычислений. Чтобы сменить режим, просто выберите этот пункт меню (например, нажав кнопку мыши в ситуации, показанной на рис 3.14, включите ручной режим).

Режим вычислений устанавливается независимо для каждого документа Одновременно могут быть открыты несколько документов, вычисляемых в различных режимах

Преимущества и недостатки каждого режима очевидны. С одной стороны, автоматические вычисления упрощают работу с документом, поскольку результаты расчетов появляются в реальном времени, и пользователь имеет возможность анализировать их сразу. С другой стороны, если вычисления сложные, то они могут отнимать много времени (что особенно заметно на компьютерах с не слишком мощным процессором и небольшим объемом оперативной памяти). Поэтому зачастую, чтобы продолжить редактирование документа, требуется довольно длительное ожидание завершения расчетов В частности, если поменять какое-либо выражение в начале большого документа, которое влияет на последующие вычисления, то все они пересчитываются заново. В таких случаях часто удобнее редактировать текст в ручном режиме, а вычисления включать по мере необходимости.

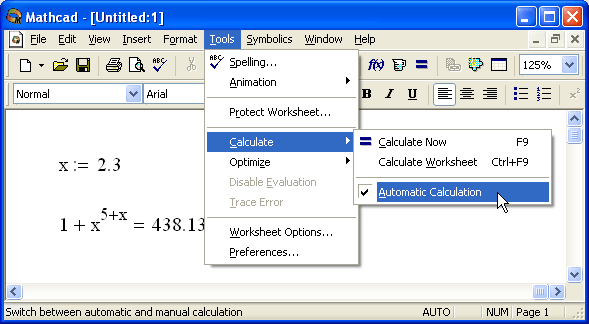
Рис. 3.14. Выбор режима вычислений

Интеграция работы с различными приложениями (Exel, Word). Примеры работы с файлами данных.

Экспортировать данные из таблицы Excel в матрицу MathCAD можно просто скопировав их и вставив затем в пустую таблицу ввода. Однако провести обратную операцию (т.е. данные из матрицы MathCAD экспортировать в Excel) используя таблицу ввода (Input Table) не получится. Для выполнения этой задачи следует задействовать таблицу Excel как компонент MathCAD. Компонентами в MathCAD называются приложения или объекты из других приложений, которые могут принимать непосредственное участие в работе создаваемого вычислительного алгоритма. Учитывая глобальность распространенности таких систем, как Excel или MatLab, возможность MathCAD осуществлять с ними согласованную работу просто неоценима, т.к. это значительно расширяет потенциал всех этих программ. Именно по этой причине создатели MathCAD посвятили целый раздел Центра Ресурсов (Extending MathCAD — подробно здесь мы его обсуждать не будем) примерам по использованию компонентов.

Особенности работы с анимацией в системе MathCAD.

  Mathcad имеет встроенную переменную FRAME, чье единственное назначение - управление анимациями:

• Создайте объект, чей вид зависит от FRAME.

• Выберите Windows->Animation->Create для вызова диалогового окна.

• Заключите в выделяющий пунктирный прямоугольник часть рабочего документа, которую нужно анимировать.

• Установите нижние и верхние границы FRAME.

• В поле At (Темп) введите значение скорости воспроизведения (кадр/сек).

• Выберите Animate. Сейчас анимация только создается.

• Сохраните анимацию как AVI файл (Save as).

• Воспроизведите сохраненную анимацию Windows->Animation-> Playback.

Во многих случаях самый зрелищный способ представления результатов математических расчетов — это анимация. Mathcad позволяет создавать анимационные ролики и сохранять их в видеофайлах.

Основной принцип анимации в Mathcad — покадровая анимация. Ролик анимации — это просто последовательность кадров, представляющих собой некоторый участок документа, который выделяется пользователем. Расчеты производятся обособленно для каждого кадра, причем формулы и графики, которые в нем содержатся, должны быть функцией от номера кадра. Номер кадра задается системной переменной FRAME, которая может принимать лишь натуральные значения. По умолчанию, если не включен режим подготовки анимации, FRAME=0.

Рассмотрим последовательность действий для создания ролика анимации, например демонстрирующего перемещение гармонической бегущей волны. При этом каждый момент времени будет задаваться переменной FRAME.

Введите в документ необходимые выражения и графики, в которых участвует переменная номера кадра FRAME. Подготовьте часть документа, которую Вы желаете сделать анимацией, таким образом, чтобы она находилась в поле Вашего зрения на экране. В нашем примере подготовка сводится к определению функции f (x, t) :=sin(x-t) и создании ее Декартова графика у (x, FRAME) .

Выполните команду Tools / Animation / Record (Сервис / Анимация / Запись).

В диалоговом окне Animate (Анимация) задайте номер первого кадра в поле From (От), номер последнего кадра в поле То (До) и скорость анимации в поле At (Скорость) в кадрах в секунду (рис. 16.58).

Выделите протаскиванием указателя мыши при нажатой левой кнопке мыши область в документе, которая станет роликом анимации.

В диалоговом окне Animate (Анимация) нажмите кнопку Animate (Анимация). После этого в окошке диалогового окна Animate (Анимация) будут появляться результаты расчетов выделенной области, сопровождающиеся выводом текущего значения переменной FRAME. По окончании этого процесса на экране появится окно проигрывателя анимации (рис. 16.59).

Запустите просмотр анимации в проигрывателе нажатием кнопки воспроизведения в левом нижнем углу окна проигрывателя.

В случае если вид анимации Вас устраивает, сохраните ее в виде видеофайла, нажав кнопку Save As (Сохранить как) в диалоговом окне Animate (Анимация). В появившемся диалоговом окне Save Animation (Сохранить анимацию) обычным для Windows способом укажите имя файла и его расположение на диске.

• 

Рис. 16.58. Начало создания анимации

Закройте диалог Animate (Анимация) нажатием кнопки Cancel (Отмена) или кнопки управления его окном.Сохраненный видеофайл можно использовать за пределами Mathcad. Скорее всего, если в проводнике Windows дважды щелкнуть на имени этого файла, он будет загружен в проигрыватель видеофайлов Windows, и Вы увидите его на экране компьютера. Таким образом, запуская видеофайлы обычным образом, можно устроить красочную презентацию результатов работы как на своем, так и на другом компьютере.

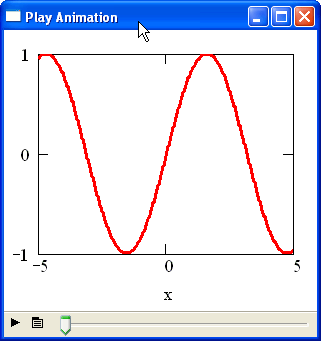
Рис. 16.59. Просмотр созданного ролика анимации

При создании файлов анимации допускается выбирать программу видеосжатия (кодек) и качество компрессии. Делается это с помощью кнопки Options (Опции) в диалоговом окне Animate (Анимация).

Работа с комплексными числами в системе MathCAD.

Большинство операций в среде Mathcad по умолчанию осуществляются над комплексными числами. Комплексное число является суммой действительного и мнимого числа, получающегося путем умножения любого действительного числа на мнимую единицу (imaginary unit) i. По определению, i2=-1.

Чтобы ввести мнимое число, например 3i:

Введите действительный сомножитель (3).

Введите символ "i" или "j" непосредственно после него.

Для ввода мнимой единицы надо нажать клавиши <1>, <i.>. Если просто ввести символ "i", то Mathcad интерпретирует его как переменную i. Кроме того, мнимая единица имеет вид 1i, только когда соответствующая формула выделена. В противном случае мнимая единица отображается просто как i (рис. 4.1).

Комплексное число можно ввести в виде обычной суммы действительной и мнимой частей или в виде любого выражения, содержащего мнимое число. Примеры ввода и вывода комплексных чисел иллюстрируются листингом 4.3.

Для работы с комплексными числами имеются несколько простых функций и операторов (см. разд. "Функции работы с комплексными числами" гл. 10), действие которых показано в листинге 4.4.

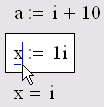
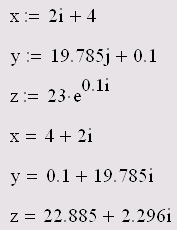
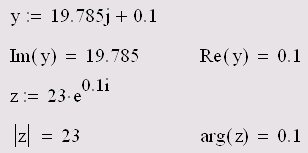
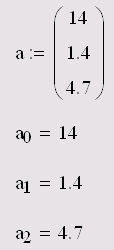
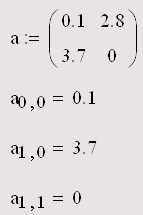
Можно выводить мнимую единицу в результатах вычислений не как i, а как j. Для смены представления выберите нужное в списке Imaginary Value (Мнимое значение) диалогового окна Result Format (Формат результата), доступного по команде Format / Result / Display Options (Формат / Результат / Опции отображения).

Работа с векторами и матрицами в системе MathCad.

4.3. Массивы

Массивами (arrays) называют упорядоченные последовательности чисел или элементов массива. Доступ к любому элементу массива возможен по его индексу, т. е. номеру в последовательности чисел (в листинге 4.10 а — это массив, ах — его элемент). Применение массивов чрезвычайно эффективно в математических расчетах.

В Mathcad условно выделяются два типа массивов:

векторы (одноиндексные массивы, листинг 4.10), матрицы (двухиндекс-ные, листинг 4.11) и тензоры (многоиндексные);

ранжированные переменные (range variables) — векторы, элементы которых определенным образом зависят от их индекса.

Листинг 4.11. Двумерный массив (матрица)

Работа с диапазонными переменными в системе MathCad.

Переменные диапазона или дискретные переменные можно задать двумя способами:

1) <идентификатор> := <Nнач> .. <Nкон>;

2) <идентификатор> := <Nнач>, <Nслед> .. <Nкон>.

Здесь <идентификатор> – имя переменной диапазона, <Nнач> и <Nкон> – соответственно начальное и конечное значения переменной, <Nслед> – следующее за <Nнач> значение переменной.

Знак . . – единый символ, для его ввода удобно использовать кнопку на панели Calculate или Matrix (рисунок 3.1).

Первый способ используется для определения переменных диапазона с целым шагом (+1): если <Nкон> больше <Nнач>, то шаг равен +1 и, наоборот, при <Nкон> меньше <Nнач> шаг равен 1.

Второй способ задает переменную диапазона с шагом, не равным 1.

П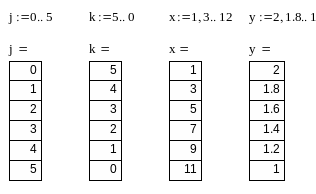 ример 1.

Таким образом, переменная диапазона в системе MathCAD представляет собой аналог арифметической прогрессии в математике.

Использование переменных диапазона

Переменные диапазона обычно используются при решении трех типов задач:

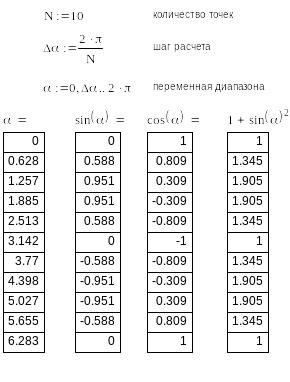
1. расчет табличных значений выражений, например:

2. переменную диапазона с целым шагом удобно использовать в качестве индексов векторов и матриц (см. п. 3.2);

3. п еременные диапазона позволяют организовать в программе итерации и рекурсии

Решение систем нелинейных алгебраических уравнений.

Вычисление корней численными методами включает два основных этапа:

      отделение корней;

      уточнение корней до заданной точности.

Решение систем уравнений

В зависимости от того, какие функции входят в систему уравнений, можно выделить два класса систем:

      алгебраические системы уравнений;

      трансцендентные системы уравнений.

Среди алгебраических систем уравнений особое место занимают системы линейных алгебраических уравнений (СЛАУ).

Системы линейных алгебраических уравнений

Системой линейных алгебраических уравнений (СЛАУ) называется система вида:

В матричном виде систему можно записать как

,

где   – матрица размерности  ,   – вектор с   проекциями.

Для вычисления решения СЛАУ следует использовать функцию lsolve, обращение к которой имеет вид: lsolve(А,b), где А – матрица системы,   – вектор правой части.

Решение систем нелинейных уравнений

MathCAD дает возможность находить решение системы уравнений численными методами, при этом максимальное число уравнений в MathCAD2001iдоведено до 200.

Для решения системы уравнений необходимо выполнить следующие этапы.

Задание начального приближения для всех неизвестных, входящих в систему уравнений. При небольшом числе неизвестных этот этап можно выполнить графически, как показано в примере.

Пример. Дана система уравнений:

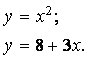
Определить начальные приближения для решений этой системы.

 

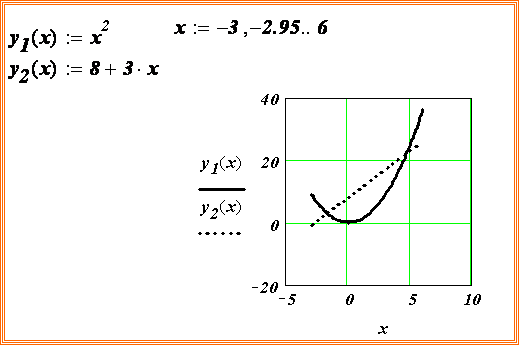
 Видно, что система имеет два решения: для первого решения в качестве начального приближения может быть принята точка (-2, 2), а для второго решения – точка (5, 20). 

Вычисление решения системы уравнений с заданной точностью. Для этого используется уже известный вычислительный блок Given.

Функция Find вычисляет решение системы уравнений с заданной точностью, и вызов этой функции имеет вид Find(x), где x – список переменных, по которым ищется решение. Начальные значения этим переменным задаются в блоке < Начальные условия >. Число аргументов функции должно быть равно числу неизвестных.

Следующие выражения недопустимы внутри блока решения:

      ограничения со знаком ;

      дискретная переменная или выражения, содержащие дискретную переменную в любой форме;

      блоки решения уравнений не могут быть вложены друг в друга, каждый блок может иметь только одно ключевое слово Given и имя функции Find (илиMinerr).

Пример. Используя блок Given, вычислить все решения системы предыдущего примера. Выполнить проверку найденных решений.

 

Пример. Используя функцию  , вычислите решение системы уравнений

 

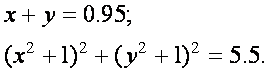
Решение уравнений функции одной и нескольких переменных.

Графическое решение систем уравнений.

Решение уравнений в общем виде.

Для решения одного уравнения с одним неизвестным используется функция root. Аргументами этой функции являются выражение и переменная, входящая в выражение. Ищется значение переменной, при котором выражение обращается в ноль. Функция возвращает значение переменной, которое обращает выражение в ноль.

root( f(z), z)

Возвращает значение z, при котором выражение или функция f(z) обращается в 0. Оба аргумента этой функции должны быть скалярами. Функция возвращает  скаляр.

Первый аргумент есть либо функция, определенная где-либо в рабочем документе, или выражение. Выражение должно возвращать скалярные значения.

Второй аргумент — имя переменной, которое используется в выражении. Это та переменная, варьируя которую Mathcad будет пытаться обратить выражение в ноль. Этой переменной перед использованием функции root необходимо присвоить числовое значение. Mathcad использует его как начальное приближение при поиске корня.

Рассмотрим пример, как найти a — решение уравнения e^x = x³. Для этого выполните следующие шаги:

• Определите начальное значение переменной x. Введите x:3. Выбор начального приближения влияет на корень, возвращаемый Mathcad (если выражение имеет несколько корней).

• Определите выражение, которое должно быть обращено в ноль. Для этого перепишите уравнение e^x = x³ в виде x³ - e^x = 0. Левая часть этого выражения и является вторым аргументом функцииroot

• Определите переменную a как корень уравнения. Для этого введите a:root(x^3[Space]-e^x[Space],x).

• Напечатайте a=, чтобы увидеть значение корня.

При использовании функции root имейте в виду следующее:

• Удостоверьтесь, что переменной присвоено начальное значение до начала использования функцииroot.

• Для выражения с несколькими корнями, например x² - 1 = 0, начальное значение определяет корень, который будет найден Mathcad. На Рисунке 1 приведен пример, в котором функция rootвозвращает различные значения, каждое из которых зависит от начального приближения.

• Mathcad позволяет находить как комплексные, так и вещественные корни. Для поиска комплексного корня следует взять в качестве начального приближения комплексное число.

• Задача решения уравнения вида f(x) = g(x) эквивалентна задаче поиска корня выражения f(x) - g(x) =0. Для этого функция root может быть использована следующим образом:

root(f(x) - g(x), x)

Функция root предназначена для решения одного уравнения с одним неизвестным. Для решения систем уравнений используйте методику, описанную в следующем разделе “Системы уравнений”. Для символьного решения уравнений или нахождения точного численного решения уравнения в терминах элементарных функций выберите Решить относительно переменной из меню Символика. См. Главу “Символьные вычисления”.

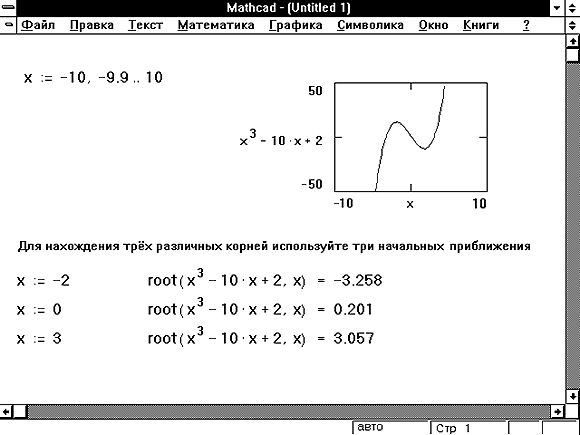
Рисунок 1: Использование графика и функции root для поиска корней уравнения.

Что делать, когда функция root не сходится

Mathcad в функции root использует для поиска корня метод секущей. Начальное значение, присвоенное переменной x, становится первым приближением к искомому корню. Когда значение выражения f(x) при очередном приближении становится меньше значения встроенной переменной TOL, корень считается найденным, и функция root возвращает результат.

Если после многих итераций Mathcad не может найти подходящего приближения, то появляется сообщение об ошибке “отсутствует сходимость”. Эта ошибка может быть вызвана следующими причинами:

• Уравнение не имеет корней.

• Корни уравнения расположены далеко от начального приближения.

• Выражение имеет локальные максимумы или минимумы между начальным приближением и корнями.

• Выражение имеет разрывы между начальным приближением и корнями.

• Выражение имеет комплексный корень, но начальное приближение было вещественным (или наоборот).

Чтобы установить причину ошибки, исследуйте график f(x). Он поможет выяснить наличие корней уравнения f(x)=0 и, если они есть, то определить приблизительно их значения. Чем точнее выбрано начальное приближение корня, тем быстрее функция root будет сходиться к точному значению. roots;using plots to find

Некоторые советы по использованию функции root

В этом разделе приведены несколько советов по использованию функции root:

• Для изменения точности, с которой функция root ищет корень, можно изменить значение встроенной переменной TOL. Если значение TOL увеличивается, функция root будет сходиться быстрее, но ответ будет менее точен. Если значение TOL уменьшается, функция root будет сходиться медленнее, но ответ будет более точен. Чтобы изменить значение TOL в определенной точке рабочего документа, используйте определение вида TOL := 0.01. Чтобы изменить значение TOL для всего рабочего документа, выберите из меню Математика команду Встроенные переменные и введите подходящее значение в поле TOL. Нажав “OK”,  выберите из меню Математика командуПересчитать всё, чтобы обновить все вычисления в рабочем документе с использованием нового значения переменной TOL.

• Если уравнение имеет несколько корней, пробуйте использовать различные начальные приближения, чтобы найти их. Использование графика функции полезно для нахождения числа корней выражения, их расположения и определения подходящих начальных приближений. Рисунок 1 показывает пример. Если два корня расположены близко друг от друга, можно уменьшить TOL, чтобы различить их.

• Если f(x) имеет малый наклон около искомого корня, функция может сходиться к значению r, отстоящему от корня достаточно далеко . В таких случаях для нахождения более точного значения корня необходимо уменьшить значение TOL. Другой вариант заключается в замене уравненияf(x)=0 на g(x)=0, где

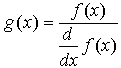
• Для выражения f(x) с известным корнем a нахождение дополнительных корней f(x) эквивалентно поиску корней уравнения h(x)=0, где h(x)=f(x)/(x-a). Подобный приём полезен для нахождения корней, расположенных близко друг к другу. Часто бывает проще искать корень выражения h(x), определенного выше, чем пробовать искать другой корень уравнения f(x)=0, выбирая различные начальные приближения.

Решение уравнений с параметром

Предположим, что нужно решать уравнение многократно при изменении одного из параметров этого уравнения. Например, пусть требуется решить уравнение для нескольких различных значений параметраa. Самый простой способ состоит в определении функции

f( a, x) := root(e^x - a x², x)

Чтобы решить уравнение для конкретного значения параметра a, присвойте значение параметру a и начальное значение переменной x как аргументам этой функции. Затем найдите искомое значение корня, вводя выражение f(a,x)=.

Рисунок 2 показывает пример того, как такая функция может использоваться для нахождения корней исследуемого уравнения при различных значениях параметра. Обратите внимание, что, хотя начальное значение x непосредственно входит в определение функции, нет необходимости определять его в другом месте рабочего документа.

Рисунок 2: Определение функции пользователя с функцией root.

Нахождение корней полинома

Для нахождения корней выражения, имеющего вид

v_nxⁿ +...+ v₂x² + v₁x + v₀,

лучше использовать функцию polyroots, нежели root. В отличие от функции root, функция polyroots не требует начального приближения. Кроме того, функция polyroots возвращает сразу все корни, как вещественные, так и комплексные. На Рисунках 3 и 4 приведены примеры использования функцииpolyroots.

polyroots(v)

Возвращает корни полинома степени . Коэффициенты полинома находятся в векторе v длины n+1. Возвращает вектор длины n, состоящий из корней полинома.

Функция polyroots всегда возвращает значения корней полинома, найденные численно. Чтобы находить корни символьно, используйте команду Решить относительно переменной из меню Символика. См. Главу  “Символьные вычисления”.

Рисунок 3: Использование функции polyroots для решения задачи, изображенной на Рисунке 1.

Рисунок 4: Использование функции polyroots для поиска корней полинома.

Приближенное решение уравнений.

Функция Minner очень похожа на функцию Find (использует тот же алгоритм). Если в результате поиска не может быть получено дальнейшее уточнение текущего приближения к решению, Minner возвращает это приближение. Функция Find в этом случае возвращает сообщение об ошибке. Правила использования функции Minner такие же, как и функции Find.

Minerr(z1, z2, . . .)

Возвращает приближенное решение системы уравнений. Число аргументов должно быть равно числу неизвестных.

Если Minner используется в блоке решения уравнений, необходимо всегда включать дополнительную проверку достоверности результатов.

Иногда приходится заменять задачу определения корней системы уравнений задачей поиска экстремума функции многих переменных. Например, когда невозможно найти решение с помощью функции Find, можно попытаться потребовать вместо точного выполнения уравнений условий минимизировать их невязку. Для этого следует в вычислительном блоке вместо функции Find использовать функцию Minerr, имеющую тот же самый набор параметров. Она также должна находиться в пределах вычислительного блока:

x1:=C1 ... хм: =Cм — начальные значения для неизвестных.

Given — ключевое слово.

Система алгебраических уравнений и неравенств, записанная логическими операторами.

Minerr (x1,... ,хм) — приближенное решение системы относительно переменных х1;... ,хм, минимизирующее невязку системы уравнений.

В функции Minerr реализованы те же самые алгоритмы, что и в функции Find, иным является только условие завершения работы численного метода. Поэтому пользователь может тем же самым образом, с помощью контекстного меню (см. разд. 8.4), выбирать численный алгоритм приближенного решения для функции Minerr.

Пример использования функции Minerr показан в листинге 8.9. Как видно, достаточно заменить в вычислительном блоке имя функции на Minerr, чтобы вместо точного (с точностью до TOL) получить приближенное решение уравнения, заданного после ключевого слова Given.

истинг 8.9 демонстрирует приближенное решение уравнения kx2+y2:=0, которое при любом значении коэффициента k имеет единственный точный корень (х=0,у=0). Тем не менее, при попытке решить его функцией Find для больших k, порядка принятых в листинге, происходит генерация ошибки "No solution was found" (Решение не найдено). Это связано с иным поведением функции f (x,y)=kx2+y2 вблизи ее корня, по сравнению с функциями, приводимыми в качестве примеров выше в этой главе (см. рис. 8.1, 8.2). В отличие от них, f (х,у) не пересекает плоскость f (х,у)=о, а лишь касается ее (рис. 8.7) в точке (х=0,у=0). Поэтому и найти корень изложенными в предыдущем разделе градиентными методами сложнее, поскольку вблизи корня производные f (х,у) близки к нулю, и итерации могут уводить предполагаемое решение далеко от корня.

Ситуация еще более ухудшается, если наряду с корнем типа касания (см. рис. 8.7) имеются (возможно, весьма удаленные) корни типа пересечения. Тогда попытка решить уравнение или систему уравнений с помощью функции Find может приводить к нахождению корня второго типа, даже если начальное приближение было взято очень близко к первому. Поэтому если Вы предполагаете, что система уравнений имеет корень типа касания, намного предпочтительнее использовать функцию Minerr, тем более, что всегда есть возможность проверить правильность решения уравнений простой подстановкой в них полученного решения (см. листинг 8.6).

В листинге 8.9 мы рассмотрели пример нахождения существующего решения уравнения. Приведем в заключение пример нахождения функцией Minerr приближенного решения несовместной системы уравнений и неравенств (листинг 8.10). Решение, выдаваемое функцией Minerr, минимизирует невязку данной системы.

Согласно своему математическому смыслу, функция Minerr может применяться для построения регрессии серии данных по закону, заданному пользователем (см. разд. 15.2).

Как видно из листинга, в качестве результата выдаются значения переменных, наилучшим образом удовлетворяющие уравнению и неравенствам внутри вычислительного блока. Внимательный читатель может обнаружить, что решение, выдаваемое функцией Minerr в рассматриваемом примере, не является единственным, поскольку множество пар значений (х,у) в равной степени минимизирует невязку данной системы уравнений и неравенств. Поэтому для различных начальных значений будут получаться разные решения, подобно тому как разные решения выдаются функцией Find в случае бесконечного множества корней (см. обсуждение листинга 8.6 в разд. 8.3). Еще более опасен случай, когда имеются всего несколько локальных минимумов функции невязки. Тогда неудачно выбранное начальное приближение приведет к выдаче именно этого локального минимума, несмотря на то, что другой (глобальный) минимум невязки может удовлетворять системе гораздо лучше.

Особенности расчета цепей переменного тока.

ОДНОФАЗНЫЕ ЦЕПИ ПЕРЕМЕННОГО ТОКА Задача 7. Цепь состоит из источника переменной ЭДС и трех ветвей, в каждой из которых резистор, конденсатор и катушка индуктивности. Вторая и третья ветви соединены параллельно между собой, последовательно с ними включена первая ветвь. Рассчитайте все токи и напряжения, полную, активную и реактивную мощности. Постройте векторную диаграмму. Определите действующие значения всех токов и напряжений. Импеданс k--ой ветви, содержащей последовательно соединенные резистор rk, конденсатор Ck и катушку индуктивности Lk, равен: Если ветви 2 и 3 соединены параллельно, а ветвь 1 --- последовательно с ними, то импеданс цепи: Неизвестные токи и напряжения найдем из закона Ома: Это позволяет построить векторную диаграмму цепи, рассчитать комплекс полной мощности. Решение задачи представлено в файле 04.mcd. Задача 8. Добавьте к предыдущей цепи четвертую ветвь параллельно источнику. Величины сопротивления, емкости и индуктивности подберите сами. Рассчитайте цепь, постройте векторную диаграмму. Задача 9. Решите задачу 7 для случая, когда первая и третья ветви состоят их резистора, конденсатора и катушки индуктивности, соединенных параллельно. Постройте векторную диаграмму. ВВЕРХ

. 4. ТРЕХФАЗНЫЕ ЦЕПИ Задача 10. Имеется четырехпроводная трехфазная цепь с несимметричной нагрузкой. Определите комплексы токов во всех линейных и нейтральном проводах, их модули, вычислите мощность, постройте векторные диаграммы. Из законов Кирхгофа получаем систему: Для ее решения создают две матрицы A и B, затем получают третью матрицу TOK:=A-1· B, элементами которой являются комплексы токов (документ 05.mcd). Их модули равны действующим значениям токов.

Работа с символьным процессором.

Системы компьютерной алгебры снабжаются специальным процессором для выполнения аналитических (символьных) вычислений. Его основой является ядро, хранящее всю совокупность формул и формульных преобразований, с помощью которых производятся аналитические вычисления. Чем больше этих формул в ядре, тем надежней работа символьного процессора и тем вероятнее, что поставленная задача будет решена, если такое решение существует в принципе (что бывает далеко не всегда).

Ядро символьного процессора системы MathCAD - несколько упрощенный вариант ядра известной системы символьной математики Maple V фирмы Waterloo Maple Software, у которой фирма MathSoft (разработчик MathCAD) приобрела лицензию на его применение, благодаря чему MathCAD стала (начиная с версии 3. 0) системой символьной математики. Символьные вычисления выполняются столь же просто (для пользователя), как вычисление квадрата х.

Символьные операции можно выполнять двумя способами:

• Непосредственно в командном режиме (используя операции меню Символы);

• С помощью операторов символьного преобразования (используя палитру инструментов Символы  ).

Рассмотрим первый способ.

Выделение выражений для символьных вычислений

Чтобы символьные операции выполнялись, процессору необходимо указать, над каким выражением эти операции должны производиться, т. е. надо выделить выражение. Для ряда операций следует не только указать выражение, к которому они относятся, но и наметить переменную, относительно которой выполняется та или иная символьная операция. Само выражение в таком случае не выделяется.

Таким образом, для выполнения операций с символьным процессором нужно выделить объект (целое выражение или его часть) синими сплошными линиями.

Символьные операции разбиты на пять характерных разделов. Первыми идут наиболее часто используемые операции. Они могут выполняться с выражениями, содержащими комплексные числа или имеющими решения в комплексном виде.

Символьные операции

 Операции с выделенными выражениями

Если в документе есть выделенное выражение, то с ним можно выполнять различные операции, представленные ниже:

Расчеты - преобразовать выражение с выбором вида преобразований из подменю;

Символические [Shift] F9 - выполнить символьное преобразование выделенного выражения;

С плавающей запятой… - вычислить выделенное выражение в вещественных числах;

Комплексные - выполнить вычисления в комплексном виде;

Упростить - упростить выделенное выражение с выполнением таких операций, как сокращение подобных слагаемых, приведение к общему знаменателю, использование основных тригонометрических тождеств и т д.;

Расширить - раскрыть выражение [например, для (Х + Y) (Х - Y) получаем X ²- Y ²];

Фактор - разложить число или выражение на множители [например, X ²- Y ² даст (Х + Y) (Х - Y)];

Подобные - собрать слагаемые, подобные выделенному выражению, которое может быть отдельной переменной или функцией со своим аргументом (результатом будет выражение, полиномиальное относительно выбранного выражения);

Коэффициенты Полинома - по заданной переменной найти коэффициенты полинома, аппроксимирующего выражение, в котором эта переменная использована.

Операции с выделенными переменными

Для ряда операций надо знать, относительно какой переменной они выполняются. В этом случае необходимо выделить переменную, установив на ней маркер ввода. После этого становятся доступными следующие операции подменю Переменные:

Вычислить - найти значения выделенной переменной, при которых содержащее ее выражение становится равным нулю;

Замена - заменить указанную переменную содержимым буфера обмена;

Дифференциалы - дифференцировать выражение, содержащее выделенную переменную, по этой переменной (остальные переменные рассматриваются как константы);

Интеграция - интегрировать все выражение, содержащее переменную, по этой переменной;

Разложить на составляющие... - найти несколько членов разложения выражения в ряд Тейлора относительно выделенной переменной;

Преобразование в Частичные Доли - разложить на элементарные дроби выражение, которое рассматривается как рациональная дробь относительно выделенной переменной.

Операции с выделенными матрицами

Операции с выделенными матрицами представлены позицией подменю Матрицы, которая имеет свое подменю со следующими операциями:

Транспонирование - получить транспонированную матрицу;

Инвертирование - создать обратную матрицу;

Определитель - вычислить детерминант (определитель) матрицы.

Результаты символьных операций с матрицами часто оказываются чрезмерно громоздкими и поэтому плохо обозримы.

Операции преобразования

В позиции Преобразование содержится раздел операций преобразования, создающий подменю со следующими возможностями:

Фурье - выполнить прямое преобразование Фурье относительно выделенной переменной;

Фурье Обратное - выполнить обратное преобразование Фурье относительно выделенной переменной;

Лапласа - выполнить прямое преобразование Лапласа относительно выделенной переменной (результат - функция переменной s);

Лапласа Обратное - выполнить обратное преобразование Лапласа относительно выделенной переменной (результат - функция

переменной t);

Z - выполнить прямое Z-преобразование выражения относительно выделенной переменной (результат - функция переменной z);

Обратное Z - выполнить обратное Z-преобразование относительно выделенной переменной (результат - функция переменной n) .

Стиль представления результатов вычислений

 На наглядность вычислений влияет стиль представления их результатов. Следующая команда позволяет задать тот или иной стиль:

Стиль Вычислений... - задать вывод результата символьной операции под основным выражением, рядом с ним или вместо него (Рисунок 9).

 

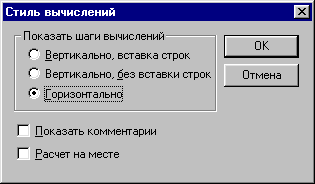
Рисунок 9.

 

Примеры символьных операций в командном режиме

Большинство символьных операций легко выполняются, так что ниже мы остановимся лишь на некоторых примерах. Символьная операция Расчеты обеспечивает работу с математическими выражениями, содержащими встроенные в систему функции и представленными в различном виде: полиномиальном, дробно-рациональном, в виде сумм и произведений, производных и интегралов и т. д. (Рисунок 10).

 

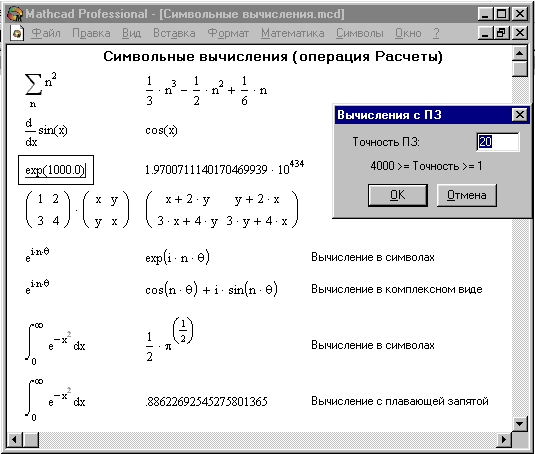
Рисунок 10.

Операция стремится произвести все возможные численные вычисления и представить выражение в наиболее простом виде. Она возможна над матрицами с символьными элементами. Производные и определенные интегралы, символьные значения которых вычисляются, должны быть представлены в своей естественной форме.

Особо следует отметить возможность выполнения численных вычислений с повышенной точностью - 20 знаков после запятой. Для перехода в такой режим вычислений нужно числовые константы в вычисляемых объектах задавать с обязательным указанием десятичной точки, например 10.0 или 3.0, а не 10 или 3. Этот признак является указанием на проведение вычислений такого типа.

На Рисунке 10 показаны типовые примеры действия операции Расчеты.

Здесь слева показаны исходные выражения, подвергаемые символьным преобразованиям, а справа - результат этих преобразований.

Операция Расчеты одна из самых мощных. Как видно из Рисунка 6, она позволяет в символьном виде вычислять суммы (и произведения) рядов, производные и неопределенные интегралы, выполнять символьные и численные операции с матрицами.

Эта операция содержит подменю. Команда Символические тут наиболее важная. Назначение других команд очевидно: они нужны, если результат требуется получить в форме комплексного или действительного числа. К примеру, если вы хотите вместо числа получить 3.141..., используйте команду С плавающей запятой…. В режиме символьных вычислений результат может превосходить машинную бесконечность системы - см. пример на вычисление ехр(1000.0) на Рисунке 10. При этом число точных значащих цифр результата практически не ограничено (или, точнее говоря, зависит от емкости ОЗУ).

Операция Разложить на составляющие... возвращает разложение в ряд Тейлора выражения относительно выделенной переменной с заданным по запросу числом членов ряда n (число определяется по степеням ряда). По умолчанию задано п = 6. В разложении указывается остаточная погрешность разложения. На Рисунке 11 представлено применение этой операции для разложения функции  . Минимальная погрешность получается при малых х (см. графическое представление функции и ее ряда).

 

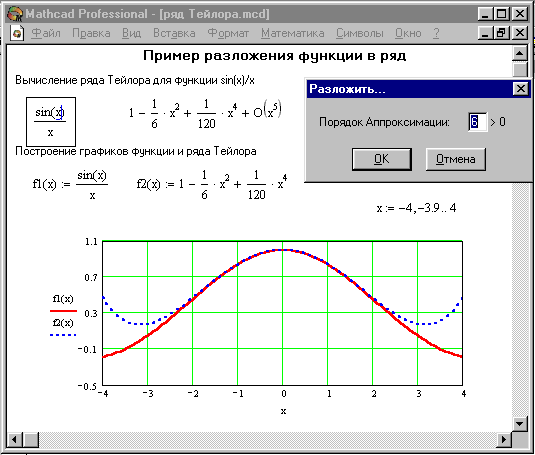
Рисунок 11.

Операторы вычисления пределов функций

Для вычисления пределов функций в систему введен символьный оператор limit. Помимо ввода с наборной панели Матанализ, его в трех формах можно ввести нажатием следующих комбинаций клавиш:

[Ctrl] L - ввод шаблона оператора вычисления предела функции при х, стремящемся к заданному значению,

[Ctrl] A - ввод шаблона вычисления предела функции слева от заданной точки,

[Ctrl] B - ввод шаблона вычисления предела функции справа от заданной точки.

На Рисунке 12 показаны примеры вычисления пределов. При вычислении пределов нужно заполнить шаблоны, входящие в главный шаблон для вычисления пределов, а затем ввести функцию, имя переменной, по которой ищется предел, и значение переменной - аргумента функции.

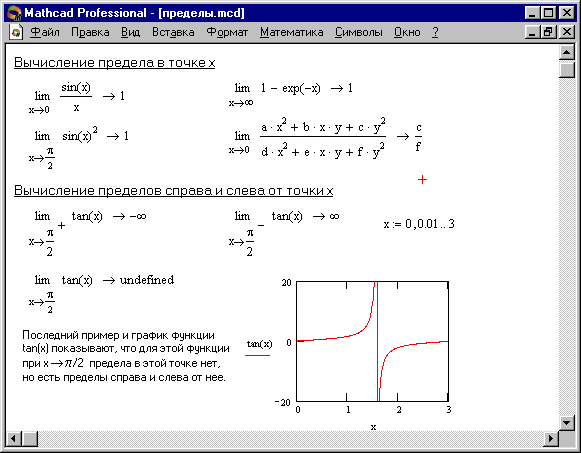
Рисунок 12.

 

Для получения результата установите после блока вычисления предела стрелку с острием, направленным вправо. Предел (если он существует) будет вычислен и появится в шаблоне у острия стрелки. Если функция не имеет предела, вместо результата появится надпись Undefine.

Задание операторов пользователя. Операторы символьного преобразования.

Еще одна экзотическая возможность, присущая новым версиям системы MathCAD, - задание новых операторов пользователя. Такой оператор задается практически так же, как функция пользователя, но вместо имени выбирается какой-либо подходящий знак. Например, можно задать оператор деления в виде:

 - задание нового оператора деления;

 - применение функции деления;

 - применение нового оператора деления.

При кажущейся простоте такого задания здесь есть проблемы. Встроенные в систему операторы нельзя переопределить. Поэтому набор доступных знаков для обозначения новых операторов ограничен. Нельзя задать новый оператор деления знаком / (он уже использован), но можно взять знак   поскольку этот символ системой не используется.

Вторая проблема связана с вводом символа нового оператора. Скорее всего, его напрямую ввести нельзя. Придется воспользоваться типовыми приемами ввода новых символов в документы Windows. Один из этих приемов - использование приложения, выдающего таблицу символов, с возможностью его экспорта из этой таблицы в документ другого приложения (в нашем случае - в документ MathCAD).

Можно также воспользоваться подходящим знаком из набора MATH SYMBOL, имеющегося в составе Шпаргалок, доступ к которым дает Ресурс Центр ( Ресурс Центр  Справочный стол и краткое руководство  Дополнительные математические символы). На Рисунке 8 показан такой вариант задания нового оператора пользователя. Для перетаскивания знака можно скопировать его в буфер обмена с помощью операции Копировать, а затем ввести в документ, используя операцию Вставка.

После того как оператор задан, его можно использовать, как функцию и как оператор. Примеры показаны на Рисунке 13.

 

Рисунок 13.

 Для применения нового оператора надо вывести его шаблон с помощью панели математических знаков (она также показана Рисунке 13). В нашем случае следует нажать кнопку   этой панели - она выводит особый шаблон вида      . Введите операнды, например 6 и 3 в крайние прямоугольники, а символ оператора - в средний. Поставив после этой конструкции знак равенства, увидите результат - число 2.

Можно задать и другие операторы, например, для работы с одним операндом. Так, вы можете задать оператор для пересчета значения температуры по шкале Цельсия, с тем чтобы определить соответствующее ему значение по шкале Фаренгейта, следующим образом

Затем, используя кнопку   наборной панели символов отношения, можно выполнять операцию пересчета в виде.

Есть области математики и физики, где задание новых операторов необходимо, поскольку является частью специфического языка их описания.

Линейная интерполяция. Операторы и функции.

Простейшим случаем локальной интерполяции является линейная интерполяция, когда в качестве интерполяционной функции выбирается полином первой степени, то есть узловые точки соединяются прямой линией.

Линейная интерполяция на Mathcad’е осуществляется с помощью встроенной функции linterp.

Пусть требуется провести линейную интерполяцию функции sin(x) на интервале [0..6], используя пять узлов интерполяции, и вычислить значения функции в четырех точках Xk

Задаем интервал изменения x и число узловых точек

   

Определяем шаг изменения x: 

Вычисляем координаты узлов и значения функции в них:

 

Проводим линейную интерполяцию: 

Вычислим значение интерполяционной функции в заданных точках и сравним их с точными значениями

Как видно, результаты интерполяции отличаются от точных значений функции незначительно.

Интерполяция сплайнами. Операторы и функции.

В настоящее время среди методов локальной интерполяции наибольшее распространение получила интерполяция сплайнами (от английского слова spline – гибкая линейка). При этом строится интерполяционный полином третьей степени, проходящий через все заданные узлы и имеющий непрерывные первую и вторую производные. На каждом интервале   интерполирующая функция является полиномом третьей степени

и удовлетворяет условиям

 (3.1).

Если всего n узлов, то интервалов –  . Значит, требуется определить   неизвестных коэффициентов полиномов. Условие дает нам n уравнений. Условие непрерывности функции и ее первых двух производных во внутренних узлах интервала дает дополнительно  уравнений

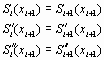
Всего имеем   различных уравнений. Два недостающих уравнения можно получить, задавая условия на краях интервала. В частности, можно потребовать нулевой кривизны функции на краях интервала, то есть  .

Задавая различные условия на концах интервала, можно получить разные сплайны.

Решим задачу об интерполяции синуса с помощью сплайнов. Для этого воспользуемся встроенной функцией interp(VS,x,y,z). Переменные x и y задают координаты узловых точек, z является аргументом функции, VS определяет тип граничных условий на концах интервала.

Определим интерполяционные функции для трех типов кубического сплайна

 

 

 

Вычисляем значения интерполяционных функций в заданных точках и сравниваем результаты с точными значениями

       

Обратите внимание, что результаты интерполяции различными типами кубических сплайнов практически не отличаются во внутренних точках интервала и совпадают с точными значениями функции. Вблизи краев интервала отличие становится более заметным, а при экстраполяции за пределы заданного интервала различные типы сплайнов дают существенно разные результаты. Для большей наглядности представим результаты на графиках

Убедимся в том, что первые и вторые производные сплайна непрерывны

Но производные более высоких порядков уже не являются непрерывными

Интерполяция

Простейшая задача интерполяции заключается в следующем. Для заданных n + 1 точек x_i = х₀, х₁, . . ., х_n, которые называютсяузлами интерполяции, и значений в этих точках некоторой функции f(x_i) = y₀, y₁, . . ., y_n построить полином  (х) (интерполяционный полином) степени n вида

(

принимающий в узлах интерполяции х_i те же значения y_i, что и функция f(x_i):

i = 0, 1, ..., n.

Глобальная интерполяция

Простейшим видом глобальной интерполяции является параболическая интерполяция, когда, используя описанные выше условия (2), для отыскания неизвестных n + 1 коэффициентов а₀, а₁, . . ., а_n выражения (1) получают систему из n + 1 уравнений:

.

(3)

Интерполяционная формула Лагранжа:

(4)

Для построения интерполяционной формулы Лагранжа в Mathcad удобно использовать функцию if

if(cond, tval, fval)

Возвращает значение tval, если cond отличен от 0 (истина). Возвращает значение fval, если cond равен 0 (ложь).

Часто интерполирование ведется для функций, заданных таблично с равноотстоящими значениями аргумента (h_i = x_i+1 - x_i = const). Введем предварительно понятие конечных разностей:

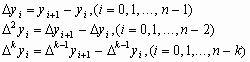
С учетом введенных обозначений первая интерполяционная формула Ньютона имеет вид:

(5)

Вторая интерполяционная формула имеет вид:

(6)

Однако, интерполяция при большом числе узлов приводит к необходимости работать с многочленами высокой степени (например, 50-й или даже 100-й), что неприемлемо как с точки зрения вычислений, так и из-за склонности таких многочленов к осцилляции (колебаниям) между узлами сетки. Поэтому на практике часто используют интерполяцию кусочными многочленами (или локальную интерполяцию).

Локальная интерполяция

При локальной интерполяции между различными узлами выбираются различные многочлены невысокой степени. В среде Mathcad есть для этого инструментарий: средства линейной интерполяции (функция linterp) и интерполяции сплайном (функция interp) - линейным (lspline), параболическим (pspline) и кубическим (cspline). Рисунок 4 показывает некоторые примеры локальной интерполяции.

 

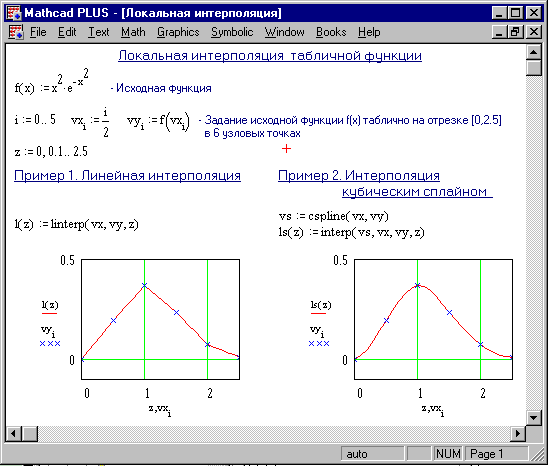
Рисунок 4. Локальная интерполяция

 

linterp(vx, vy, x)	Использует векторы данных vx и vy, чтобы возвратить линейно интерполируемое значение у, соответствующее третьему аргументу x.
lspline(vx, vy)pspline(vx, vy)cspline(vx, vy)	Все эти функции возвращают вектор коэффициентов вторых производных, который мы будем называть vs. Вектор vs, используется в функции interp:
interp(vs, vx, vy, x)	Возвращает интерполируемое значение у, соответствующее аргументу х.

Аппроксимация функций. Встроенные функции для аппроксимации.

Аппроксимацией (приближением) функции  называется нахождение такой функции  (аппроксимирующей функции), которая была бы близка заданной. Критерии близости функций  и  могут быть различные.

В том случае, когда приближение строится на дискретном наборе точек, аппроксимацию называют точечной или дискретной.

В том случае, когда аппроксимация проводится на непрерывном множестве точек (отрезке), аппроксимация называется непрерывнойили интегральной. Примером такой аппроксимации может служить разложение функции в ряд Тейлора, то есть замена некоторой функции степенным многочленом.

Наиболее часто встречающим видом точечной аппроксимации является интерполяция (в широком смысле).

Пусть задан дискретный набор точек  , называемых узлами интерполяции, причем среди этих точек нет совпадающих, а также значения функции  в этих точках. Требуется построить функцию  , проходящую через все заданные узлы. Таким образом, критерием близости функции является  .

В качестве функции  обычно выбирается полином, который называют интерполяционным полиномом.

В том случае, когда полином един для всей области интерполяции, говорят, что интерполяция глобальная.

В тех случаях, когда между различными узлами полиномы различны, говорят о кусочной или локальной интерполяции.

Найдя интерполяционный полином, мы можем вычислить значения функции  между узлами (провести интерполяцию в узком смысле слова), а также определить значение функции  даже за пределами заданного интервала (провести экстраполяцию).

Следует иметь в виду, что точность экстраполяции обычно очень невелика.

Одномерная линейная аппроксимация.

При проведении научно-технических расчетов часто используются зависимости вида у (х), причем число точек этих зависимостей ограничено. Неизбежно возникает задача получения приемлемой представительности функций в промежутках между узловыми точками (интерполяция) и за их пределами (экстраполяция). Эта задача решается аппроксимацией исходной зависимости, т. е. ее подменой какой-либо достаточно простой функцией. Система MathCAD предоставляет возможность аппроксимации двух типов: кусочно-линейной и сплайновой.

При кусочно-линейной интерполяции, или аппроксимации, вычисления дополнительных точек выполняются по линейной зависимости. Графически это означает просто соединение узловых точек отрезками прямых, для чего используется следующая функция: linterp(VX, VY, х) Для заданных векторов VX и VY узловых точек и заданного аргумента х эта функция возвращает значение функции при ее линейной аппроксимации. При экстраполяции используются отрезки прямых с наклоном, соответствующим наклону крайних отрезков при линейной интерполяции.

Одномерная сплайн-интерполяция и сплайн-аппроксимация.

При небольшом числе узловых точек (менее 10) линейная интерполяция оказывается довольно грубой. Для целей экстраполяции функция linterp не предназначена и за пределами области определения может вести себя непредсказуемо.

Гораздо лучшие результаты дает сплайн-аппроксимация. При ней исходная функция заменяется отрезками кубических полиномов, проходящих через три смежные узловые точки. Коэффициенты полиномов рассчитываются так, чтобы непрерывными были первая и вторая производные.

Для осуществления сплайновой аппроксимации система MathCAD предлагает четыре встроенные функции. Три из них служат для получения векторов вторых производных сплайн-функций при различном виде интерполяции: cspline(VX, VY) — возвращает вектор VS вторых производных при приближении в опорных точках к кубическому полиному; pspline(VX, VY) — возвращает вектор VS вторых производных при приближении к опорным точкам параболической кривой; lspline(VX, VY) — возвращает вектор VS вторых производных при приближении к опорным точкам прямой. Наконец, четвертая функция interp(VS, VX, VY, x)-возвращает значение у (х) для заданных векторов VS, VX, VY и заданного значения x.

Таким образом, сплайн-аппроксимация проводится в два этапа. На первом с помощью функций cspline, pspline или Ispline отыскивается вектор вторых производных функции у (х), заданной векторами VX и VY ее значений (абсцисс и ординат). Затем, на втором этапе для каждой искомой точки вычисляется значение у (х) спомощью функции interp.

Двумерная линейная сплайн-интерполяция и сплайн-аппроксимация.

Для повышения качества построения ЗD-графиков имеется возможность осуществления двумерной сплайн-интерполяции. Это позволяет существенно повысить представительность сложных графиков SD-функций, в том числе контурных.

Интерполяция функции 2-х переменных проводится также в два этапа: 1. Вычисляется вектор VS вторых производных в опорных точках с помощью функций cspline(Mxy,Mz), pspline(Mxy,Mz), lspline(Mxy,Mz) . Здесь Mxy - матрица размера n*2, сторки которой определяют по диагонали (x,y)координаты прямоугольной сетки, Mz - матрица размера n*n значений функции в узлах вышеопределенной сетки. 2. Вычисление с помощью функции interp(VS,Mxy,Mz,V). Здесь V - вектор координат (x,y).

На рисунке справа показан график функции 2-х переменных после проведения двумерной сплайн-интерполяции, а слева - без нее.

Предсказание функций.

Если необходимо оценить значения функции в точках не принадлежащих отрезку [x₀, x_n], используйте функцию predict (Рисунок 5).

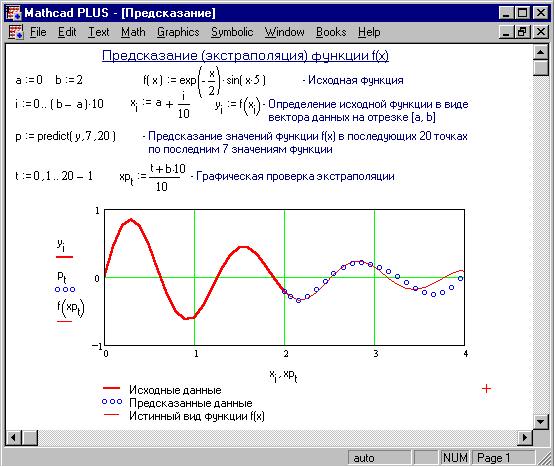
Рисунок 5. Экстраполяция функций

predict(v, m, n)

Возвращает n предсказанных значений, основанных на m последовательных значениях вектора данных v.

Чтение, запись и редактирование текстовых файлов.

Важный компонент ввода-вывода — это ввод-вывод во внешние файлы. Ввод внешних данных в документы Mathcad применяется чаще вывода, поскольку Mathcad имеет гораздо лучшие возможности представления результатов расчетов, чем многие пользовательские программы. Для общения с внешними файлами данных в Mathcad имеется несколько разных способов. Самый простой из них — использовать имеющееся семейство встроенных функций.

16.6.1. Текстовые файлы

Перечислим встроенные функции для работы с текстовыми файлами:

READPRN( " file") — чтение данных в матрицу из текстового файла;

WRITEPRN( "file") — запись данных в текстовый файл;

APPENDPRN("file") — дозапись данных в существующий текстовый файл;

file — путь к файлу.

Можно задавать как полный путь к файлу, например, С:\Мои документы, так и относительный, имея в виду, что он будет отсчитываться от папки, в которой находится файл с документом Mathcad.

Примеры использования встроенных функций иллюстрируются листингами 16.5—16.7. Результат действия листингов 16.5 и 16.7 можно понять, просмотрев получающиеся текстовые файлы, например с помощью Блокнота Windows (рис. 16.60 и 16.61, соответственно).

Листинг 16.5. Запись матрицы I в текстовый файл

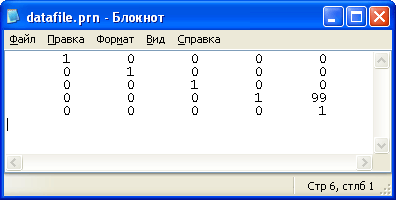
Рис. 16.60. Файл, созданный листингом 16.5

Листинг 16.6. Чтение данных из текстового файла в матрицу С

Листинг 16.7. Дозапись вектора k в соответствующий текстовый файл

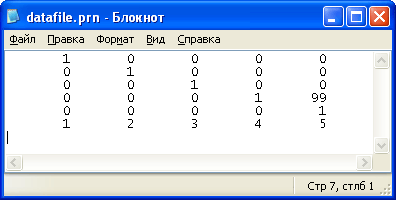
Рис. 16.61. Файл, созданный листингами 16.5 и 16.7

Обратите внимание, что если Вы выводите данные в файл, пользуясь встроенной функцией WRITEPRN, то в любом случае создается новый текстовый файл. Если даже до записи данных файл с таким именем существовал, то его содержимое будет уничтожено, заменившись новыми данными. Если Вы хотите сохранить прежнее содержимое текстового файла с данными, пользуйтесь функцией APPENDPRN. Эта встроенная функция может применяться и для создания нового файла. Иными словами, если файла с заданным именем не существовало, то он, после применения, будет создан и наполнен теми данными, которые Вами определены в документе.

Чтение и запись структурированных файлов.

В этом разделе обсуждается использование функций READPRN, WRITEPRN и APPENDPRN для работы со структурированными файлами. Структурированный файл данных — файл с фиксированным числом значений на строке. Например, если экспортировать прямоугольную область из электронной таблицы в текстовый файл, возникающие в результате строки и столбцы чисел сформируют структурированный файл.

Считывание матрицы с помощью функции READPRN

Предположим, что имеется ASCII-файл, содержащий данные, показанные ниже. Эти данные могут быть взяты из электронной таблицы или из любого другого источника.

Рисунок 4 показывает документ Mathcad, который считывает эти данные в матрицу.

Функция READPRN читает весь файл данных, определяет число строк и столбцов, и создает матрицу из этих данных.

Когда Mathcad читает данные с помощью функции READPRN:

• Каждый раз READPRN читает файл данных целиком.

• Все строки в файле данных должны содержать одинаковое количество значений. (Строки, не содержащие значений, игнорируются). Если строки в файле имеют различное число значений, Mathcad, отмечает функцию READPRN сообщением “ошибка файла”.

• Функция READPRN игнорирует текст в файле данных.

• Результатом чтения файла данных является m-на-n матрица, где m есть число строк, содержащих данные в файле, и n есть число значений в строке. Чтобы создать матрицу из значений в файле данных, используйте равенство, подобное M: = READPRN(file). Не используйте нижние индексы дляM. Функция READPRN возвращает матрицу, поэтому нижние индексы излишни.

• Чтобы читать из файла с именем, которое не совпадает с именем файловой переменной, либо из файла, находящегося не в каталоге по умолчанию, выберите Присоединить к файлу из менюФайл. Подробнее см. раздел “Импортирование данных из других каталогов”.

Предупреждение: Каждая строка в файле данных должна содержать одинаковое число значений. Если оставить промежутки там, где Mathcad ожидает значение, функция READPRN не сможет прочитать файл. Mathcad определяет конец одного и начало следующего значения, ища пробелы или запятые.

Иногда каждый столбец значений в файле данных представляет отдельную переменную. Рисунок 5 показывает, как использовать верхние индексы, чтобы создать вектор из каждого столбца в файле данных.

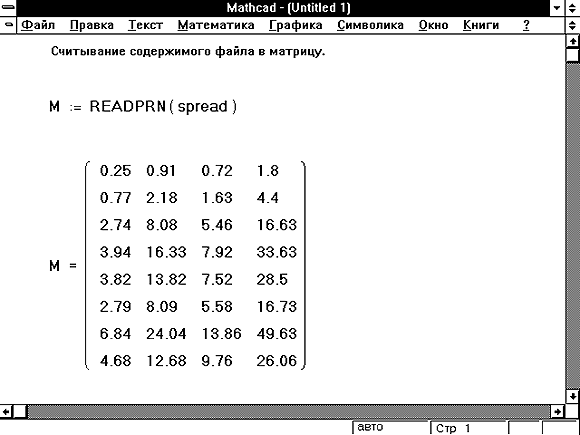
Рисунок 4: Считывание таблицы данных в матрицу.

Рисунок 5: Присваивание различным переменным значений из разных столбцов в файле данных.

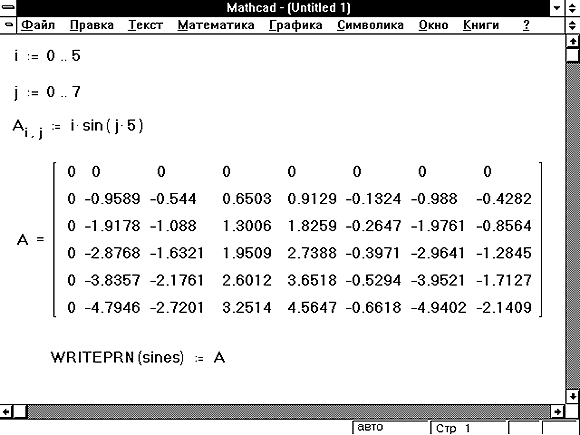
Рисунок 6: Запись данных в структурированный файл данных.

Запись данных при помощи функций WRITEPRN и APPENDPRN

Рисунок 6 показывает, как использовать функцию WRITEPRN, чтобы записать данные в структурированный файл данных.

Когда Mathcad обрабатывает документ из Рисунка 6, создается файл данных, содержащий следующие значения:

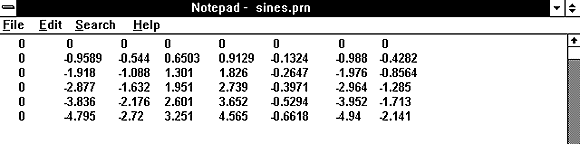
В отличие от WRITE функция WRITEPRN записывает данные в виде столбцов. Обратите внимание, что, поскольку для PRNPRECISION установлено значение четыре, числа записаны с четырьмя знаками после запятой. Поскольку значение PRNCOLWIDTH равно восьми, каждый столбец имеет ширину в восемь символов. Так как PRNPRECISION и PRNCOLWIDTH могут изменяться независимо, нужно не упустить из виду, что ширина столбца должна быть такой, чтобы разместились все необходимые цифры вместе с пробелом, разделяющим отдельные  значения.

Когда используется функция WRITEPRN:

• Равенства, содержащие WRITEPRN, должны быть следующего вида. Слева записывается WRITEPRN(file), где file — имя файловой переменной, затем следует символ определения (:=) и выражение, возвращающее матрицу. Не используйте дискретные аргументы или нижние индексы с WRITEPRN .

• Каждое новое равенство записывает новый файл. Если два равенства пишут в один файл, данные, написанные вторым равенством уничтожат данные, написанные первым. Используйте APPENDPRN, если нужно дописать значения к файлу вместо того, чтобы перезаписать файл. APPENDPRN function

• Встроенные переменные PRNCOLWIDTH и PRNPRECISION определяют формат файла данных, создаваемого Mathcad. Текущее значение PRNCOLWIDTH определяет ширину столбцов (в символах). Текущее значение PRNPRECISION определяет число используемых значащих цифр. По умолчанию PRNCOLWIDTH = 8 и PRNPRECISION = 4. Чтобы изменить эти значения, выберитеВстроенные переменные из меню Математика или поместите соответствующие определения в документ Mathcad выше места использования WRITEPRN, как показано на Рисунке 7.

• Если записываемый массив  является  составным  (чьи элементы являются сами массивами), либо комплекснозначным, то тогда WRITEPRN создаст не просто ASCII-файл, а файл специального формата, который навряд ли будет читаем другими прикладными программами. Этот файл может, однако, читаться функцией READPRN.

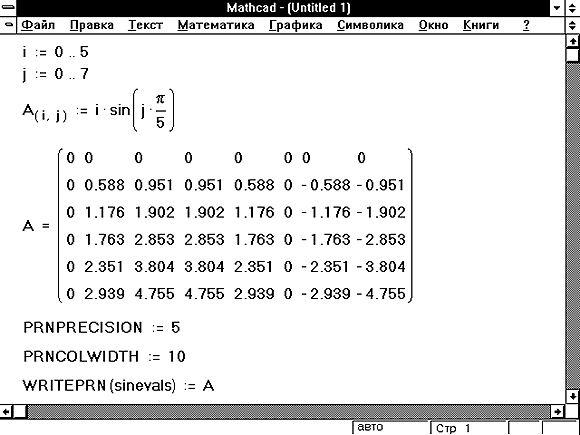
Рисунок 7: Документ, который создаёт файл данных со столбцами шириной в 10 символов, содержащий числа с 5 значащими цифрами.

Используя функцию augment, можно объединять отдельные переменные в массивы, и записывать их все в файл данных. Рисунок 8 показывает, как это делать.

Рисунок 8: Запись нескольких векторов, объединённых вместе.

Преимущества использования READPRN и WRITEPRN

Использование READPRN, как правило, предпочтительнее использования READ. Когда данные структурированы в столбцы, READPRN переводит данные в Mathcad в легкодоступной форме.

Если некоторые строки в файле данных имеют большее количество значений, чем другие, данные могут быть потеряны. Используйте текстовый редактор, чтобы заменить пропущенные значения на нули перед использованием READPRN.

Функция READ используется для файлов, в которых значения одной переменной разбросаны по нескольким строкам. Таковы файлы, созданные WRITE, которая располагает столько чисел на строке, сколько строка может вместить.

Помните: используйте нижний индекс, являющийся дискретным аргументом, чтобы читать с помощьюREAD; не используйте нижний индекс, чтобы читать с помощью READPRN.

Обычно WRITEPRN производит более читаемые файлы, чем WRITE, поскольку данные в них аккуратно расположены в строках и столбцах. С другой стороны, WRITE производит меньшие файлы, чемWRITEPRN, потому что ей не нужно добавлять пробелы для выравнивания данных.

Используйте WRITE вместо WRITEPRN, когда требуется напихать так много значений, сколько возможно, в малый файл данных.

Работа с программами из нескольких частей.

Примеры в предыдущих разделах были очень простыми. В этом разделе рассмотрены примеры более сложных программ, решающих задачи, которые было бы трудно или невозможно решить без возможности программирования.

Одной из черт, определяющих гибкость методов программирования, является возможность использовать одни программные структуры внутри других. В Mathcad это можно сделать тремя путями:

• Один из операторов программы можно сделать, в свою очередь, программой.

• Можно определить программу где-нибудь в другом месте и вызывать ее из других программ так, как если бы она была подпрограммой.

• Можно определить функцию рекурсивным образом.

Остальная часть этого раздела поясняет эти методы на примерах.

Подпрограммы

Вспомнив, что программа является выражением, состоящим из операторов, каждый из которых содержит выражения, можно прийти к выводу, что оператор в программе может быть другой программой.

На Рисунке 8 приведены два примера программ, содержащих оператор, являющийся, в свою очередь, программой. Пример в правой части Рисунка 8 показывает пример вложенных программ с большим числом уровней. Вообще говоря, предел для числа уровней вложенных друг в друга программ отсутствует. С практической точки зрения программы со слишком большим числом уровней вложенности могут оказаться слишком трудными для понимания.

Одним из путей, которым многие программисты избегают нагромождения сложных программных конструкций, является перенесение сложностей в “подпрограммы.” На Рисунке 9 показано, как это можно сделать в Mathcad. Определив intsimp где-нибудь в другом месте и использовав его внутри adapt, можно сделать программу, определяющую adapt, значительно проще. Определение adapt стало бы значительно более громоздким, если бы оба вхождения intsimp в него нужно было бы заменять длиннющим определением intsimp, приведенным в верхней части рисунка.

Функция  adapt осуществляет адаптивную квадратуру или интегрирование, используя intsimp для аппроксимации площади на каждом подинтервале интегрирования. Из последней строки видно, что функция adapt вызывает сама себя, т.е. определена рекурсивно. Рекурсивные определения функций рассмотрены более подробно в следующем разделе.

Рисунок 8: Программы, операторы которых сами являются программами.

Рисунок 9: Использование подпрограммы для устранения громоздкости.

Рекурсия

Рекурсия  является одним из мощных методов программирования и заключается в определении функции через саму себя, как показано на Рисунке 10. Рекурсивные определения функций должны всегда состоять по меньшей мере из двух частей:

• начального определения, предотвращающего бесконечную рекурсию, и

• определения функции в терминах предыдущего значения функции.

Основная идея подобна идее математической индукции: если можно получить значение f(n+1) из f(n) и известно f(0), то известна и вся функция  f.

Рисунок 10: Рекурсивное определение функции.

Следует, однако, помнить, что рекурсивные определения функций далеко не всегда являются самыми эффективными в вычислительном отношении, несмотря на их краткость и элегантность. Часто оказывается, что определения, использующие операторы цикла, вычисляют нужные значения  быстрее.

Работа с программными блоками в системе MathCAD. Программные операторы.

Программа Mathcad есть частный случай выражения Mathcad. Подобно любому выражению, программа возвращает значение, если за ней следует знак равенства. Точно так же, как переменную или функцию можно определить через выражение, их можно определить и с помощью программы.

Главным различием между программой и выражением является способ задания вычислений. При использовании выражения алгоритм получения ответа должен быть описан одним оператором. В программе может быть использовано столько операторов, сколько нужно. Можно рассматривать программу как “составное выражение.”

Следующий пример показывает, как написать простую программу для вычисления  функции

Хотя этот пример настолько прост, что, может быть, и программа в этом случае не нужна, он позволяет показать, как нужно отделять друг от друга операторы, и как использовать локальный оператор присваивания “ ¬”.

• Введите левую часть определения функции и знак равенства “:=” и удостоверьтесь в том, что появилось поле ввода.

• Теперь нужно открыть панель программирования, щёлкнув по кнопке программирования в панели управления. Затем нужно нажать на панели кнопку“Add Line” или на клавиатуре клавишу ].  Появится вертикальный столбец с двумя полями ввода для занесения операторов, образующих программу. Поля ввода для дополнительных операторов открываются с помощью щелчка по кнопке “Add Line”.

• Перейдите в верхнее поле ввода, нажав клавишу [Tab]. Напечатайте z и нажмите кнопку “ ¬ ” на панели программирования или клавишу  для того, чтобы ввести “ ¬”.

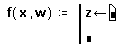
• В поле ввода справа от “ ¬ ” введите x/w.

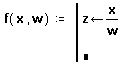
• Последнее поле ввода предназначено для задания возвращаемого функцией значения log(z).

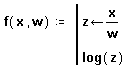
Теперь эту функцию можно использовать точно так же, как любую другую функцию. На Рисунке 1 эта функция показана вместе с функцией, ей эквивалентной, но определенной на одной строке вместо двух. Отметим, что переменная z не определена вне программы. Определение z внутри программы является локальным и действительно только внутри этой программы.

Программа может состоять из любого числа операторов. Чтобы прибавить оператор, нужно щёлкнуть по кнопке “Add Line” на панели программирования. Mathcad добавляет поле ввода внизу выделенного к этому моменту оператора. Чтобы исключить позицию ввода, ее нужно выделить, заключив в выделяющую рамку, и нажать клавишу [Del].

Рисунок 1: Определение одной и той же функции с помощью программы и через выражение.

На Рисунке 2 приведен несколько более сложный пример с формулой для корня квадратного уравнения. Хотя вычисление этого корня может быть описано одной формулой, как это показано в верхней половине рисунка, однако удобнее вычислять его с помощью последовательности простых операторов, как показано в нижней половине рисунка. Это позволяет избежать редактирования громоздких формул.

Рисунок 2: Определение более сложной функции в виде выражения и в виде программы.

Таким образом, программа Mathcad есть выражение, состоящее из последовательности операторов, каждый из которых является, в свою очередь, выражением. Как и любое другое выражение, программа Mathcad возвращает значение. Этим значением является значение последнего выражения, выполненного программой. Возвращаться может просто число, как на Рисунках 1 и 2, или массив чисел, как на Рисунке 6, или даже их комбинация, описанная в разделе “Составные массивы” .

Нижеследующие разделы описывают использование условных операторов и различных конструкций операторов цикла для управления ходом выполнения программы.

Операторы условного выбора.

Обычно Mathcad выполняет операторы программы в порядке сверху вниз. Могут встретиться случаи, в которых какой-нибудь оператор нужно выполнить только в случае выполнения некоего условия. Этого можно добиться с помощью оператора “if”. Ниже приводится пример определения функции, задаваемой разными аналитическими соотношениями на разных участках области определения:

• Введите левую часть определения функции и знак равенства “:=” и удостоверьтесь в том, что появилось поле ввода.

• Нажмите кнопку “Add Line” на панели программирования или клавишу ].  Появится вертикальный столбец с полями ввода для операторов программы.

• Перейдите в верхнее поле ввода и щёлкните по кнопке “if” на панели программирования, либо нажмите клавишу }.

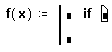
• Правое поле ввода предназначено для булевого выражения. Левое поле ввода предназначено для значения, которое будет иметь выражение, если логическое выражение в правом поле истинно.

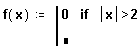
• Выделите оставшееся поле ввода и нажмите кнопку “otherwise” на панели программирования.

• Введите в оставшееся поле значение, которое программа должна возвратить в случае, если логическое выражение ложно.

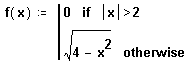
На Рисунке 3 показан график этой функции. Она имеет только два варианта возвращаемого значения и поэтому легко может быть определена с помощью встроенной функции if, как на Рисунке 3. Если же число вариантов больше двух, то использование встроенной функции if быстро становится обременительным, пример чего приведен на Рисунке 4.

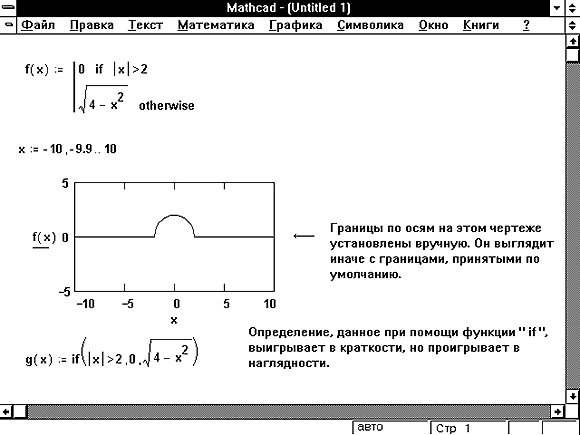
Рисунок 3: Использование оператора “if” для задания кусочно-непрерывной функции.

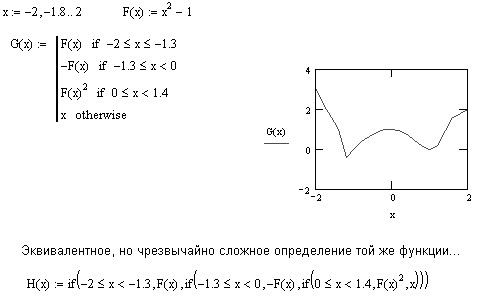
Рисунок 4: Сравнение программного оператора “if” со встроенной функцией “if”.

Разложение функции в ряд Фурье. Задача разложения.

Одним из фундаментальных положений математики, нашедшим широкое применение во многих прикладных задачах (процессы передачи информации, в теории электротехники, в исследовании движения машин, в теории корабля и др.), является возможность описания любой периодической функции f(t) с периодом Т, удовлетворяющей условиям Дирихле (согласно теореме Дирихле периодическая функция должна иметь конечное число разрывов и непрерывность производных между ними.), с помощью тригонометрического ряда Фурье:

,

(1)

где w ₁ = 2p /T - частота повторения (или частота первой гармоники); k - номер гармоники. Этот ряд содержит бесконечное число косинусных или синусных составляющих - гармоник, причем амплитуды этих составляющих a_k и b_k являются коэффициентами Фурье, определяемыми интегральными выражениями:

(2) (3)

Помимо упомянутой формы ряд Фурье можно представить в виде

,

(4)

где амплитуда А_k и фаза j _k гармоник определяются выражениями:

(5) (6)

Гармоническим анализом называют разложение функции f(t), заданной на отрезке [0, Т] в ряд Фурье или в вычислении коэффициентов Фурье a_k и b_k по формулам (2) и (3).

Гармоническим синтезом называют получение колебаний сложной формы путем суммирования их гармонических составляющих (гармоник) (Рисунок 16).

Спектром временной зависимости (функции) f(t) называется совокупность ее гармонических составляющих, образующих ряд Фурье. Спектр можно характеризовать некоторой зависимостью А_k (спектр амплитуд) и j _k (спектр фаз) от частоты w _k = kw ₁.

Спектральный анализ периодических функций заключается в нахождении амплитуды А_k и фазы j _k гармоник (косинусоид) ряда Фурье (4). Задача, обратная спектральному анализу, называется спектральным синтезом (Рисунок 17 - продолжение Рисунка 16).

Слово “классический” тут означает, что коэффициенты Фурье вычисляются прямым интегрированием тем методом, который используется в Mathcad.

Численный спектральный анализ заключается в нахождении коэффициентов a₀, a₁, ..., a_k,  b₁, b₂, ..., b_k (или A₁, A₂, ..., A_k, j ₁, j₂, ..., j _k) для периодической функции y = f(t), заданной на отрезке [0, Т] дискретными отсчетами. Он сводится к вычислению коэффициентов Фурье по формулам численного интегрирования для метода прямоугольников (см. Лабораторную работу 5)

(7)   (8)

где D t = T / N - шаг, с которым расположены абсциссы y = f(t).

Встроенные в Mathcad средства быстрого преобразования Фурье (БПФ) существенно упрощают процедуру приближенного спектрального анализа. БПФ - быстрый алгоритм переноса сведений о функции, заданной 2^m (m - целое число) отсчетами во временной области, в частотную область. Если речь идет о функции f(t), заданной действительными отсчетами, следует использовать функцию fft.

fft(v)

Возвращает прямое БПФ 2m-мерного вещественнозначного вектора v, где v - вектор, элементы которого хранят отсчеты функции f(t).

Результатом будет вектор А размерности 1 + 2^m - 1 с комплексными элементами - отсчетами в частотной области. Фактически действительная и мнимая части вектора есть коэффициенты Фурье a_k и b_k, что существенно упрощает их получение (см. Приложение 3).

Функция ifft реализует обратное БПФ:

ifft(v)

Возвращает обратное БПФ для вектора v с комплексными элементами. Вектор v имеет 1 + 2m - 1 элементов.

Результатом будет вектор А размерности 2^m с действительными элементами.

На Рисунке 18 показано применение БПФ для спектрального анализа и синтеза импульса.

 

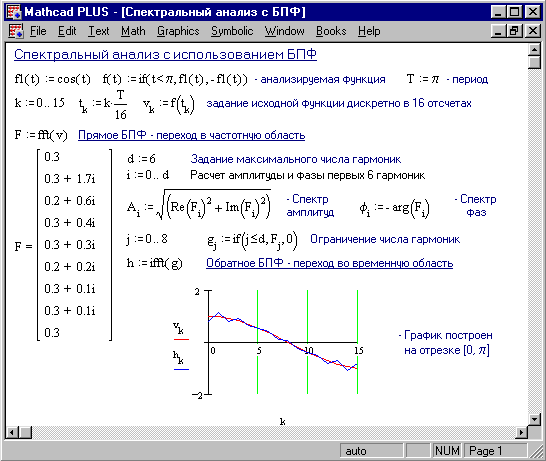
Рисунок 18. Спектральный анализ с использованием БПФ

Под фильтрацией подразумевается выделение полезного сигнала из его смеси с мешающим сигналом - шумом. Наиболее распространенный тип фильтрации - частотная фильтрация. Если известна область частот, занимаемых полезным сигналом, достаточно выделить эту область и подавить те области, которые заняты шумом.

Рисунок 19 иллюстрирует технику фильтрации с применением БПФ. Сначала синтезируется исходный сигнал, представленный 128 отсчетами вектора v. Затем к этому сигналу присоединяется шум с помощью генератора случайных чисел (функция rnd) и формируется вектор из 128 отсчетов зашумленного сигнала.

 

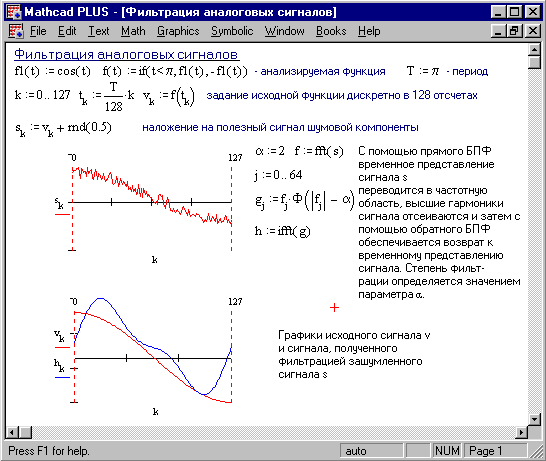
Рисунок 19. Фильтрация аналоговых сигналов

Используя прямое БПФ, сигнал с шумом преобразуется из временной области с частотную, что создает вектор f из 64 частотных составляющих. Затем выполняется фильтрующее преобразование, эффективность которого оценивается параметром a . Фильтрующее преобразование удобно выполнять с помощью функции Хевисайда

Ф(х)	Ступенчатая функция Хевисайда. Возвращает 1, если х   0; иначе 0.

Отфильтрованный сигнал (вектор g) подвергается обратному БПФ и создает вектор выходного сигнала h.

Сравнение временных зависимостей исходного и выходного сигналов, показывает, что выходной сигнал почти полностью повторяет входной и в значительной мере избавлен от высокочастотных шумовых помех, маскирующих полезный сигнал.

Решение дифференциальных уравнений. Задача Коши.

Задачу Коши можно сформулировать следующим образом: пусть дано ОДУ:

(1)

и начальное условие  . Требуется найти функцию  , удовлетворяющую как указанному уравнению, так и начальному условию.

Численное решение задачи Коши состоит в построении таблицы приближенных значений y₁, y₂, ..., y_n решения уравнения   в точках x₁, x₂, ..., x_n. Чаще всего х_i = x₀ + ih, i = 0, 1, ..., n, где h - шаг приращения переменной x, n - число интервалов решения с шагом h.

Рассмотрим здесь две группы численных методов решения задачи Коши: одношаговые и многошаговые.

Одношаговые методы

Одношаговые методы - это методы, в которых для нахождения следующей точки на кривой y = f(x) требуется информация лишь об одном предыдущем шаге. Простейшим из одношаговых методов является метод Эйлера:

, i = 0, 1, ..., n - 1.

(2)

Метод Эйлера имеет невысокую точность (порядка h).

Для достижения более высокой точности (порядка h⁴) используют метод Рунге-Кутта четвертого порядка:

, где
		(3)

Многошаговые методы

В многошаговых методах для отыскивания следующей точки кривой у = f(x) требуется информация более чем об одной из предыдущих точек.

Пусть найдены значения   в четырех последовательных точках. При этом имеются также вычисленные ранее значения правой части уравнения (1)  . Тогда схему метода Адамса можно представить в виде:

, i = 3, 4, ..., n - 1.

(4)

где конечные разности в точке  имеют вид:

(5)

Решение задачи Коши средствами Mathcad

Инструментарий для решения ОДУ (систем ОДУ) различного порядка в Mathcad представлен широким спектром встроенных функций, работа одной из которых (rkfixed - метод Рунге-Кутта (rk) четвертого порядка с фиксированным (fixed) шагом интегрирования) показана на Рисунке 9.

  

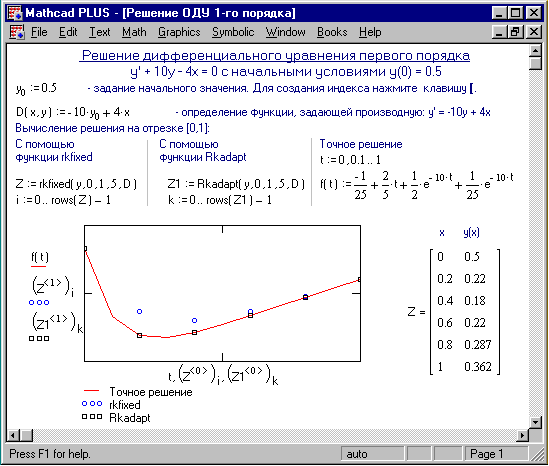
Рисунок 9. Решение ОДУ 1-го порядка

 

rkfixed(y, a, b, n, D)

Возвращает матрицу с р + 1 столбцами и n + 1 строками (р - количество уравнений или порядок уравнения, n - число шагов на интервале [a, b]) - таблицу решений системы: первый столбец - это значения аргумента х, а последующие столбцы - значения ординат решения. y - вектор начальных условий размерности n. D(x, y) - функция-вектор из nэлементов, содержащая первые производные неизвестных функций.

Можно решить задачу более точно (более быстро), если уменьшить шаг h там, где производная меняется быстро, и увеличить шаг там, где она ведет себя более спокойно. Для этого предусмотрена функция Rkadapt (adaption - адаптация). Аргументы и матрица, возвращаемая функцией Rkadapt, такие же, как при rkfixed (см. Рисунок 9). Решение системы ОДУ показано на Рисунке 11 (Пример 2).

Краевые задачи

Краевая задача формулируется следующим образом: пусть на отрезке [a, b] требуется найти решение дифференциального уравнения (для простоты изложение будем вести на примере ОДУ второго порядка):

, при граничных условиях у(а) = А, у(b) = В.

(6)

В этом случае Mathcad предлагает использовать функцию sbval, чтобы найти недостающие начальные условия в точке а.

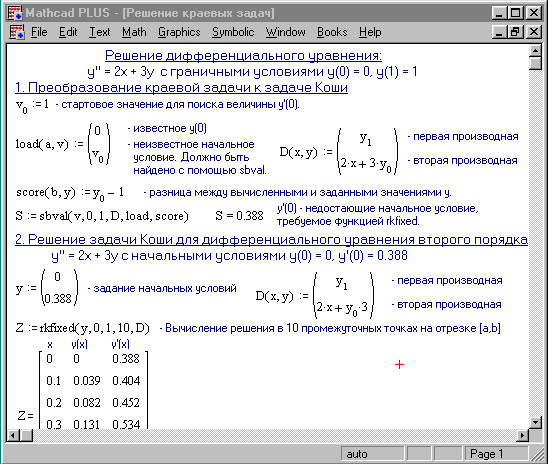
Рисунок 10. Решение краевой задачи

 

Sbval(v, а, b , D, load , score)

Возвращает вектор, содержащий недостающие начальные условия в точке а. Вектор v задает начальные приближения, а, b - граничные точки интервала решений, D(x, y) - функция-вектор с первыми производными неизвестных функций. load(а, v) - функция-вектор, возвращающая значение начальных условий в точке а.score(b, y) - функция-вектор, каждый элемент которого содержит разность между начальным условием заданным в точке b, и значением искомого решения в этой точке.

После того, как эти недостающие начальные условия будут получены, можно решать обычную задачу с начальными условиями -задачу Коши, используя любую из функций, описанных выше (Рисунок 9).Пример решения краевой задачи показан на Рисунке 10.

 

Решение систем дифференциальных уравнений.

Методика решения системы ОДУ очень похожа на методику решения ОДУ высокого порядка, которая была описана выше. Фактически можно рассматривать решение дифференциального уравнения высокого порядка как частный случай решения системы ОДУ.

Системы ОДУ первого порядка

Для того чтобы решить систему ОДУ первого порядка, необходимо:

• Определить вектор, содержащий начальные значения для каждой неизвестной функции.

• Определить функцию, возвращающую значение в виде вектора из n элементов, которые содержат первые производные каждой из неизвестных функций.

• Выбрать точки, в которых нужно найти приближенное решение.

• Передать всю эту информацию в функцию rkfixed.

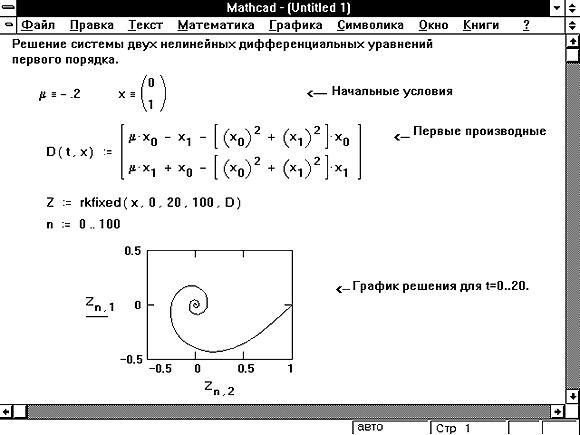
Рисунок 5: Система линейных дифференциальных уравнений первого порядка.

Функция  rkfixed вернёт матрицу, чей первый столбец содержит точки, в которых ищется приближенное решение, а остальные столбцы содержат значения найденных приближенных решений в соответствующих точках.

На Рисунке 5 приведен пример решения следующей системы ОДУ:

 x'₀(t) = m x₀(t) - x₁(t) - (x₀(t)² + x₁(t)²) x₀(t)

 x'₁(t) = m x₁(t) + x₀(t) - (x₀(t)² + x₁(t)²) x₁(t)

с начальными условиями:

x₀(0) = 0 и x₁(0) = 1

Системы дифференциальных уравнений более высокого порядка

Методика решения системы дифференциальных уравнений, каждое из которых может содержать производные от неизвестных функций выше первого порядка, та же, что описана выше. Заметим, что любое уравнение вида

x⁽ⁿ⁾ = f( t, x^(n-1), x^(n-2),..., x,...)

посредством замены

x1(t) = x(t)

x2(t) = x'(t)

...

xn(t) = x(n-1)(t)

может быть приведено к совокупности уравнений

x'1(t) = x2(t)

x'2(t) = x3(t)

...

x'n(t) = f( t, xn, xn-1,... x1,...)

Заметьте, что в приведённых выше уравнениях не встречаются производные выше первого порядка. Преобразовав подобным образом каждое из уравнений, входящих в исходную систему, получим систему с большим количеством неизвестных функций, но с производными только первого порядка. Методика решения таких систем описана в предыдущем подразделе. Пример на Рисунке 6 показывает, как поступать при решении системы дифференциальных уравнений второго порядка:

u''(t) = 2v(t)

v''(t) = 4v(t) - 2u(t)

Рисунок 6: Система линейных дифференциальных уравнений второго порядка.

Функция rkfixed возвращает матрицу, в которой:

• Первый столбец содержит точки, в которых должны быть найдены решения и их производные.

• Остальные столбцы содержат значения решений и их производных, соответствующие точкам из первого столбца. Порядок, в котором появляются решение  и его производные, повторяет порядок их расположения в функции D(x,y) и векторе начальных условий y.

Метод Эйлера, модифицированный метод Эйлера.

Метод Эйлера для дифференциальных уравнений первого порядка

Решим задачу Коши для дифференциального уравнения первого порядка   методом Эйлера.

Пусть правая часть уравнения равна 

Зададим границы изменения x:   

Зададим число точек и величину шага:   

Зададим начальные условия:   

Вычислим x и y по формулам Эйлера 

Представим результат графически и сравним его с аналитическим решением 

  

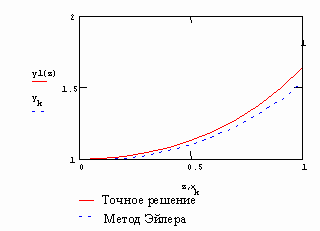
Точное аналитическое решение и решение, полученное численно, отличаются в точке x=1 на 

То есть относительная ошибка составляет 

Метод Рунге-Кутта 4-го порядка.

Дифференциальные уравнения первого порядка

Дифференциальное уравнение первого порядка — это уравнение, которое не содержит производных выше первого порядка от неизвестной функции. На Рисунке 1 показан пример того, как решить относительно простое дифференциальное уравнение:

с начальными условиями: y(0) = 4

Функция  rkfixed на Рисунке 1 использует для поиска решения метод Рунге-Кутты четвертого порядка. В результате решения получается матрица, имеющая два следующих столбца:

• Первый столбец содержит точки, в которых ищется решение дифференциального уравнения.

• Второй столбец содержит значения найденного решения в соответствующих точках.

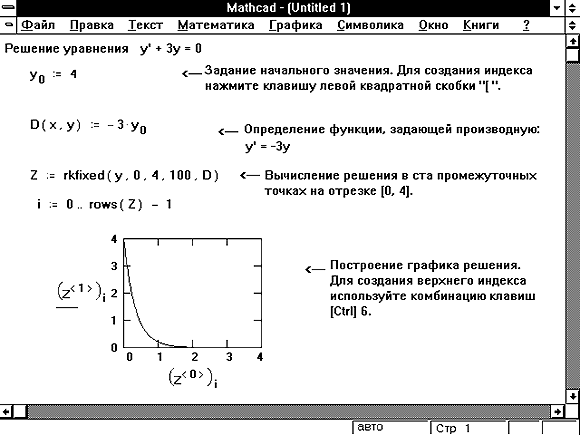
Рисунок 1: Решение дифференциального уравнения первого порядка.

Функция  rkfixed имеет следующие аргументы:

rkfixed ( y, x1, x2, npoints, D)

y =	Вектор начальных условий размерности n, где n — порядок дифференциального уравнения или число уравнений в системе (если решается система уравнений). Для дифференциального уравнения первого порядка, как, например, для уравнения, приведенного на Рисунке 1, вектор начальных значений вырождается в одну точку y0 = y(x1).
x1, x2 =	Граничные точки интервала, на котором ищется решение дифференциальных уравнений. Начальные условия, заданные в векторе y, — это значение решения в точке x1.
npoints =	Число точек (не считая начальной точки), в которых ищется приближенное решение. При помощи этого аргумента определяется число строк (1 + npoints) в матрице, возвращаемой функцией rkfixed.
D (x, y) =	Функция, возвращающая значение в виде вектора из n элементов, содержащих первые производные неизвестных функций.

Наиболее трудная часть решения дифференциального уравнения состоит в определении функции D(x, y), которая содержит вектор первых производных от неизвестных функций. В примере, приведенном на Рисунке 1, было достаточно просто разрешить уравнение относительно первой производной , и определить функцию D(x, y). Иногда, особенно в случае нелинейных дифференциальных уравнений, это может быть трудно. В таких случаях иногда удаётся разрешить уравнение относительно в символьном виде и подставить это решение в определение для функции D(x, y). Используйте для этого командуРешить относительно переменной из меню Символика.

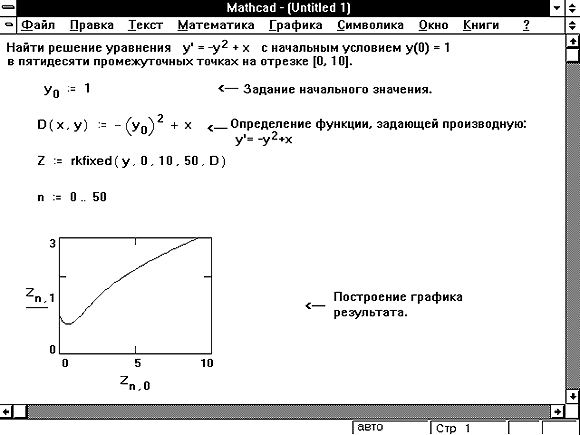
Рисунок 2: Более сложный пример, содержащий нелинейное дифференциальное уравнение.

Дифференциальные уравнения второго порядка

Как только Вы научились решать дифференциальное уравнение первого порядка, можно приступать к решению дифференциальных уравнений более высокого порядка. Мы начнем с дифференциального уравнения второго порядка. Основные отличия от уравнения первого порядка состоят в следующем:

• Вектор начальных условий y теперь состоит из двух элементов: значений функции и её первой производной в начальной точке интервала x1.

• Функция  D(t, y) является теперь вектором  с  двумя  элементами:

• Матрица, полученная в результате решения, содержит теперь три столбца: первый столбец содержит значения t, в которых ищется решение; второй столбец содержит y(t); и третий — y'(t).

Пример, приведенный на Рисунке 3, показывает, как решить следующее дифференциальное уравнение второго порядка:

y'' = -y' + 2y y(0) = 1     y'(0) = 3

Рисунок 3: Решение дифференциального уравнения второго порядка.

Уравнения более высокого порядка

Методика решения дифференциальных уравнений более высокого порядка является развитием методики, которая применялась для решения дифференциальных уравнений второго порядка. Основное различие состоит в следующем:

• Вектор начальных значений y теперь состоит из n элементов, определяющих начальные условия для искомой функции и ее производных y, y' , y'',....y^(n-1)

• Функция D является теперь вектором, содержащим  n элементов:

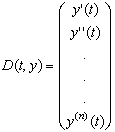
• Матрица, получаемая в результате решения, содержит теперь n столбцов: первый — для значений t,и оставшиеся столбцы — для значений y (t), y' (t), y''(t),....y^(n-1)(t).

Пример, приведенный на Рисунке 4, показывает, как решить следующее дифференциальное уравнение четвертого порядка:

y'''' - 2k²y'' + k⁴y = 0

с начальными условиями:

y (0) = 0   y' (0) = 1   y'' (0) = 2   y''''(0) = 3

Рисунок 4: Решение дифференциального уравнения более высокого порядка.
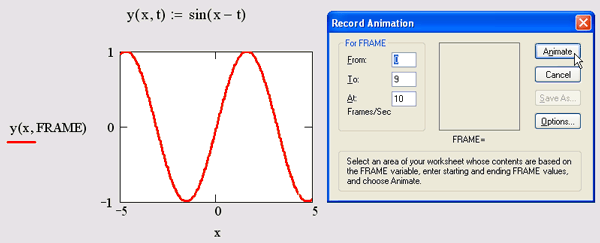
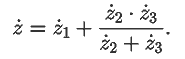
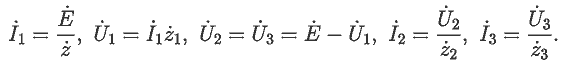
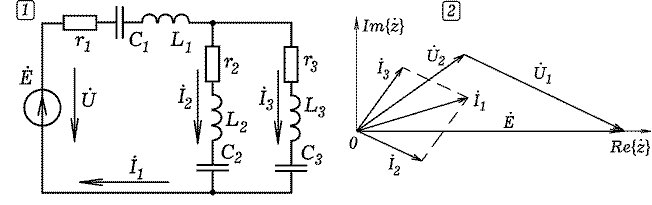
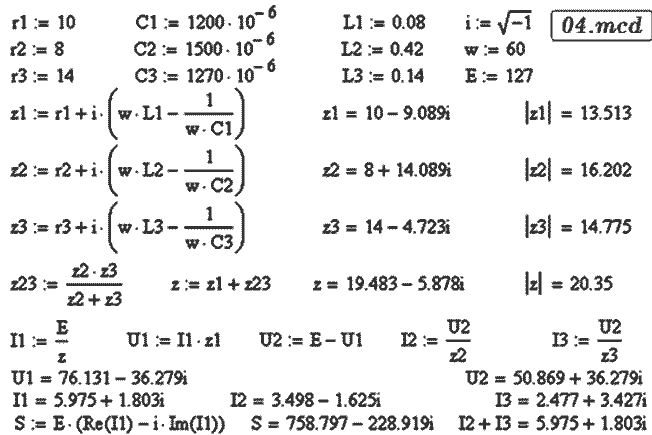
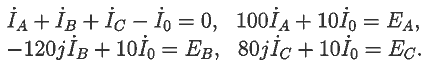
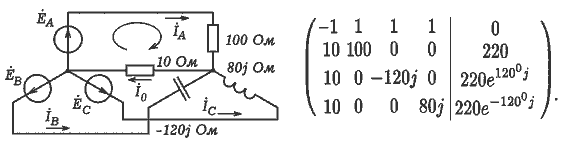
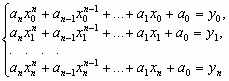