
- •1. Расчет линейной электрической цепи постоянного тока
- •1.1 Расчет токов во всех ветвях схемы методом узловых и контурных уравнений
- •1.2 Расчет токов во всех ветвях схемы методом контурных токов
- •1.3 Расчет токов во всех ветвях схемы методом наложения
- •1.4 Сравнительная оценка результатов расчетов токов в ветвях различными методами
- •1.5 Расчет баланса мощностей для заданной схемы
- •1.6 Построение потенциальной диаграммы замкнутого контура, включающего обе эдс
- •2. Расчет однофазных линейных электрических цепей переменного тока
- •2.1 Расчет реактивных сопротивлений цепи
- •2.2 Расчет полных сопротивлений в ветвях цепи
- •2.3 Расчет токов в ветвях цепи
- •2.4 Расчет напряжений на элементах заданной электрической цепи
- •2.5 Расчет показания вольтметра
- •2.6 Расчет полной мощности цепи
- •2.7 Расчет активной и реактивной мощностей приемников
- •2.8 Расчет коэффициента активной мощности цепи Cos φ
- •2.9 Уравнения мгновенных значений токов в узле а
- •2.10 Построение векторных диаграмм токов и напряжений
- •3. Расчет трехфазных линейных электрических цепей переменного тока
- •3.1 Расчет фазных сопротивлений
2.5 Расчет показания вольтметра
![]() В
В
2.6 Расчет полной мощности цепи
Рассчитаем полную
мощность источника
![]() ,
ВА
,
ВА
![]()
Активная мощность источника Рист, Вт, равна
Pis = 127,796 Вт,
Реактивная мощность источника Qист, вар, равна
Qis = 121,508 вар
2.7 Расчет активной и реактивной мощностей приемников
Рассчитаем активную
![]() ,
Вт, и реактивную
,
Вт, и реактивную
![]() ,
вар, мощности приемников двумя методами:
,
вар, мощности приемников двумя методами:
- используя значения токов и сопротивлений
![]() Вт,
Вт,
![]() вар,
вар,
- используя значения токов и напряжений
![]() Вт,
Вт,
![]() вар
вар
Анализ полученных результатов показывает, что активная и реактивная мощности приемников равны соответственно активной и реактивной составляющим полной мощности источника. Следовательно, баланс мощностей выполняется.
2.8 Расчет коэффициента активной мощности цепи Cos φ
![]()
![]()
Рассчитаем Cosφ и угол φ через найденные значения активной и реактивной составляющих полной мощности цепи
2.9 Уравнения мгновенных значений токов в узле а
i1 (t) = 3,919 sin (314 t – 140) А,
i2(t) = 1,189 sin (314 t + 1410) А,
i3(t) = 3.551 sin (314 t – 190) А
Графики мгновенных значений токов в узле А представлены в соответствии с рисунком 13.
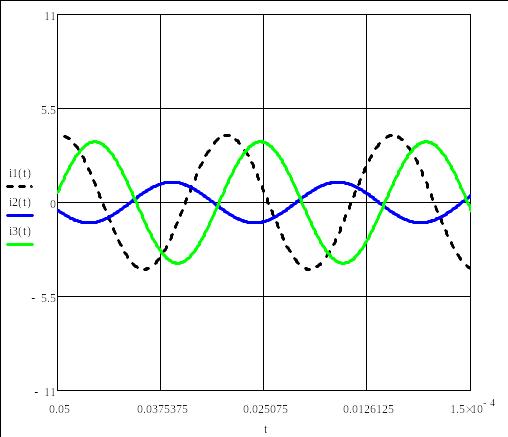
Рисунок 13 - Графики мгновенных значений токов в узле А
2.10 Построение векторных диаграмм токов и напряжений
Для построения
векторной диаграммы токов зададимся
масштабом для токов:
![]() .
Тогда длины векторов токов будут
следующими:
.
Тогда длины векторов токов будут
следующими:
![]() см,
φI
= -13,60,
см,
φI
= -13,60,
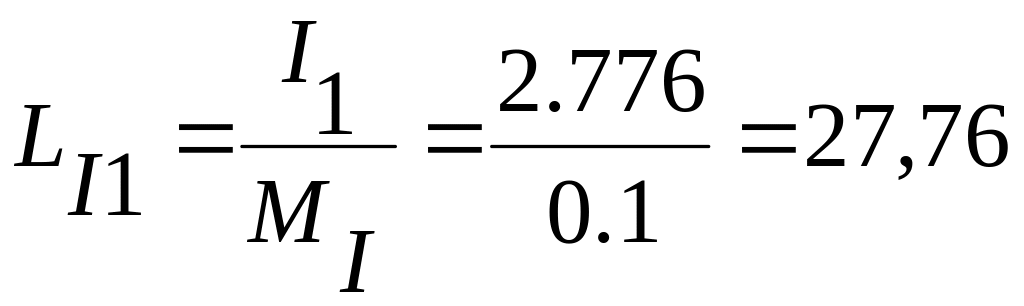 см, φI1
= -13,60,
см, φI1
= -13,60,
 см, φI2
= 141,40,
см, φI2
= 141,40,
 см φI3
= -19,30
см φI3
= -19,30
Для построения
векторной диаграммы напряжений зададимся
масштабом для напряжений:![]() .Тогда
длины векторов напряжений будут
следующими:
.Тогда
длины векторов напряжений будут
следующими:
![]() см, φU
= 300,
см, φU
= 300,
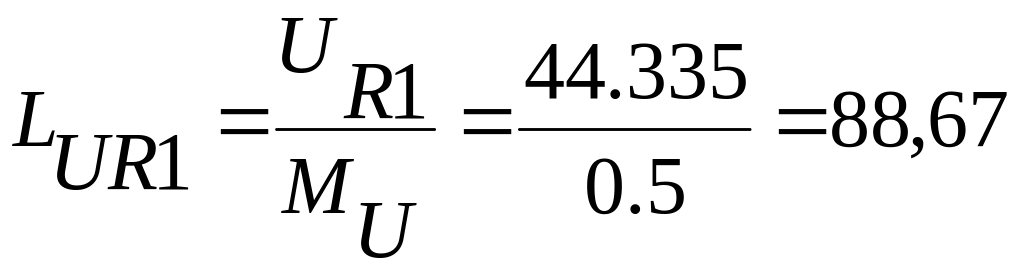 см,
φUR1
= -13,60,
см,
φUR1
= -13,60,
 см,
φUR2
= 141,40,
см,
φUR2
= 141,40,
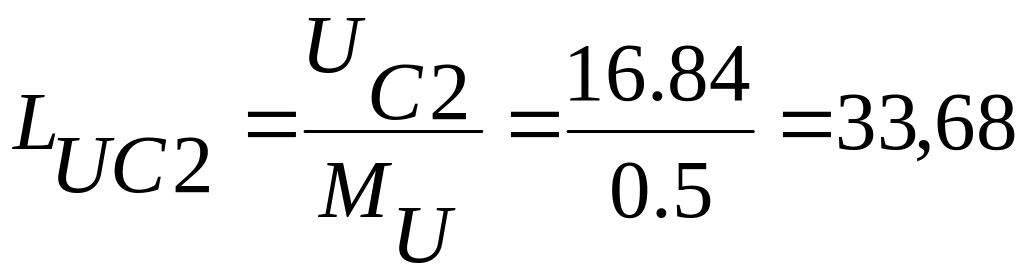 см,
φUC2
= 51,40,
см,
φUC2
= 51,40,
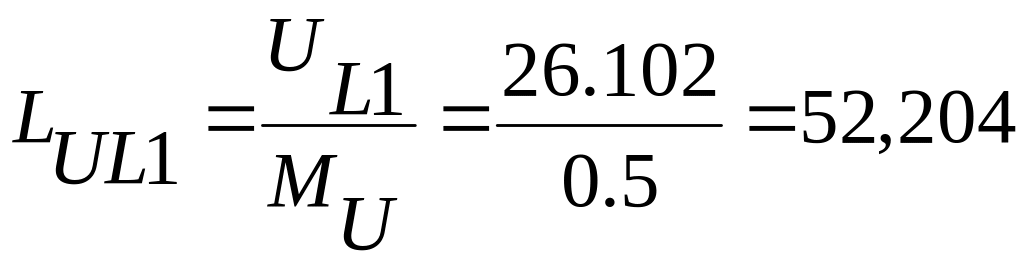 см,
φUL1
= 76,40,
см,
φUL1
= 76,40,
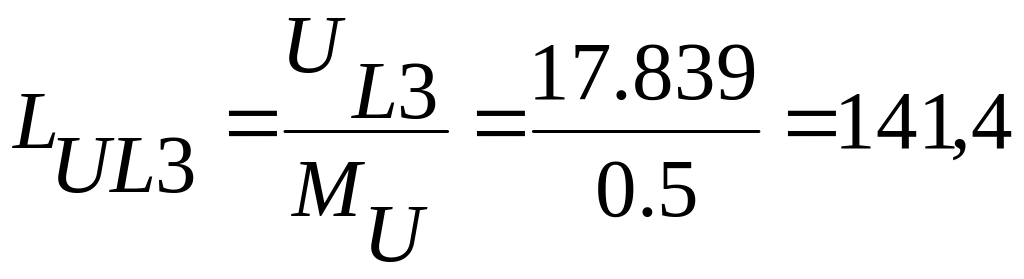 см
φUL3
= 70,70
см
φUL3
= 70,70
Зная длины векторов токов и напряжений и углы, под которыми они должны быть проведены на плоскости, строим векторную диаграмму токов и напряжений в соответствии с рисунком 14.
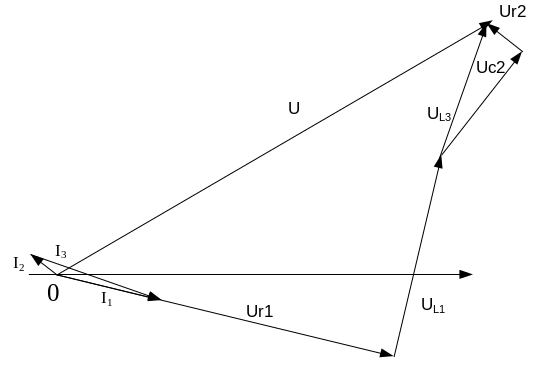
Рисунок 14 - Векторная диаграмма токов и напряжений
Векторная диаграмма приведена в приложении Б.
3. Расчет трехфазных линейных электрических цепей переменного тока
Начертить схему соединения заданных сопротивлений треугольником в трехфазной цепи, имеющей следующие числовые параметры: Uл = 660 В, RАВ=14 Ом, ХСА = 19 Ом, ХВС = 12 Ом.
Определить:
- фазные токи;
- линейные токи;
- активную, реактивную и полную мощность каждой фазы и всей трехфазной цепи;
- угол сдвига фаз между током и напряжением в каждой фазе;
- записать уравнения для мгновенных значений токов в каждой фазе и показать в масштабе на графиках закон их изменения во времени;
- начертить в масштабе векторную диаграмму токов и напряжений трехфазной цепи.
Решение. Схема соединения заданных сопротивлений треугольником в трехфазной цепи показана на рисунке 15.
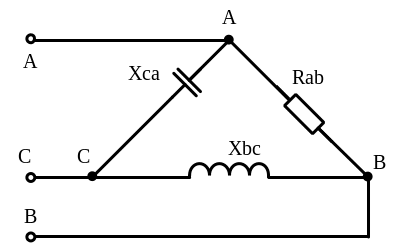
Рисунок 15 – Схема соединения заданных сопротивлений треугольником в трехфазной цепи
