3 8Расчет цилиндрических винтовых пружин малого шага

при осевом растяжении и сжатии цилиндрической пружины, навитой из круглого прута диаметра d (концевые витки в расчетах на прочность и жесткость во внимание не принимаются), средним диаметром витка D, числом витков n, углом подъема витков α (при α<5° называются пружинами малого шага) В пружинах малого шага можно пренебречь подъемом витков и считать длину витка примерно равной πD, а сам виток - расположенным в плоскости, нормальной к оси пружины; сечение прутка пружины плоскостью, содержащей ее ось, можно рассматривать как ее поперечное сечение

и шагом пружины h

Из условия равновесия отсеченной части внутренние касательные силы упругости в сечении пружины приводятся к перерезывающей силе

Q=P и крутящему моменту М_к=PD/2

Касательные напряжения кручения

максимальны в контурных точках сечения, напряжения от перерезывающей силы в

первом приближении равномерно распределены

по сечению. В точке А контура сечения суммарные касательные напряжения достигают максимума

Для большинства пружин d/2D - величина малая по сравнению с единицей: основной вид деформации - кручение, срезом можно пренебречь

И зменение продольных размеров λ определяют энергетическим методом, приравнивая работу А статически приложенной силы Р потенциальной энергии деформации U пружины. Работа внешних сил A=Pλ/2, а потенциальная энергия накапливается, главным образом, за счет кручения прутка. Крутящий М_к=PD/2 и момент инерции I_p=πd⁴/32 по длине прутка не изменяются, длина прутка l=πDn:

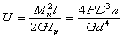
приравнивая A и U

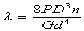
Для пружин сжатия формула справедлива лишь до полного обжатия пружины (до соприкосновения витков). После полного обжатия пружина начинает работать на осевое сжатие как прямой пустотелый брус

3 9Кручение бруса прямоугольного сечения

при кручении бруса любого некруглого сечения его поперечные сечения искривляются (депланируют) - нельзя принять гипотезу плоских сечений.

Р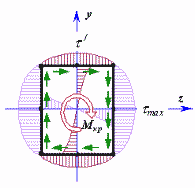 ешение задачи получено в теории упругости Сен-Венаном: касательные напряжения в контурных точках сечения возрастают от нулевых значений в углах к серединам сторон по некоторым кривым, в центре сечения равны нулю, максимального значения достигают в серединах длинных сторон

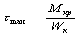
Наибольшее t на короткой стороне прямоугольника

Угол закручивания

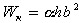
где: b - длина короткой стороны; h - длинной сторону прямоугольника; α,β,γ - коэффициенты, зависящие от соотношения сторон h и b.

41.Чистый и поперечный изгибы. Дифференциальные зависимости между изгибающими моментами, поперечными силами и интенсивностью распределенных нагрузок.

изгиб - деформация, при которой происходит искривление оси прямого бруса (изменение кривизны оси кривого бруса); в поперечных сечениях возникают изгибающие моменты. Если действует только изгибающий момент – чистый изгиб:

Если в поперечных сечениях действует изгибающий момент и поперечная сила - поперечный изгиб:

Дифференциальные зависимости

Н а выделенный элемент действуют внутренние силы, часть распределенной нагрузки интенсивности q_x (принимаем постоянной на бесконечно малой длине d_x). Условия равновесия элемента:

пренебрегая бесконечно малыми второго порядка малости: