61.Лемма Лагранжа. Дифференциальное уравнение Эйлера.

Лемма: если для непрерывной функции a(x), x=[a,b], и каждой допустимой вариации h(x), x=[a,b], выполняется равенство: то .

Доказательство [от противного]: . Для определенности . Известно, что непрерывная функция, имеющая в некоторой точке значение определенного знака, определяет знак, который она имела в этой точке некоторой окрестности. Если . Существует ε – окрестность точки . Рассмотрим .

, для любой вариации. Построим вариацию следующего вида:

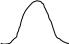
Получаем, что , а это противоречие. Ч.т.д.

Выпишем условие стационарности для простейшей задачи:

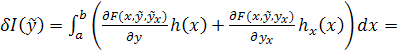
Первый интеграл перепишем, а второй проинтегрируем по частям.

.

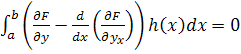, a(x) – непрерывна на [a,b].

- уравнение Эйлера. Ему удовлетворяют все слабые минимали.

62.Лемма Дюбуа – Раймона. Интегральное уравнение Эйлера.

Лемма: если для непрерывных b(x), определенных на [a,b], и всех вариаций g(x), для которых , то b(x)=const.

Доказательство: предположим, что b(x) не const, другими словами: такие, что . Для определенности положим, что

точек , что значение функции не опускается ниже средней полосы и не поднимается выше ее, т.е. для окрестности точки имеем: , для :

Сконструируем эту вариацию следующим образом:

Функция g(x), которая изображена на рисунке удовлетворяет условию вариации, т.е. .

Ч.т.д.

Согласно лемме мы получаем:

-интегральное уравнение Эйлера.

63.Присоединенная задача о минимуме. Условие Лежандра – Клебша.

Задача минимизации 2 вариации, где функция h – допустимая вариация класса С⁽¹⁾ называется присоединенной задачей о минимуме.

(*)

Если слабая минималь, то по необходимому условию . Если взять h(x)=0, то . Следовательно h(x) – решение задачи (*). Присоединенная задача и минимуме имеет решение.

Условие Лежандра – Клебша: для каждой слабой минимали, определенной на [a,b]:

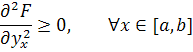
64. Исследование второй вариации. Условие Якоби. Достаточные условия слабого минимума.

Опр. Говорят, что вдоль допустимой кривой в точке сопряжена с точкой , если нетривиальное решение уравнения .В начальной точке: . Теорема Якоби. Вдоль неособой минимали на интервале нет точек, сопряжённых с точкой . Тогда уравнение Якоби тривиального решения не имеет. Теорема без доказательства. Говорят, что допустимая кривая удовлетворяет усиленному условию Лежандра–Клебша, если . Говорят, что допустимая кривая удовлетворяет условию Якоби, если вдоль неё на полуинтвервале не существует точек, сопряжённых с точкой . Эти два последних определения позволяют сформулировать достаточное условие минимума. Допустимая кривая является слабой минималью, если она является экстремалью. Выполнено усиленное условие Лежандра–Клебша и усиленное условие Якоби.