39. Пусть имеется функция , определенная на множестве . Требуется найти

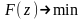при условиях ,

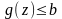где , .

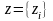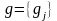Методы решения этой задачи разделяются на методы, базирующиеся на методе градиента, и методы, использующие штрафные функции.

Метод возможных направлений

Этот метод работает с ограничениями типа строгих неравенств. Он основан на анализе возможных направлений в окрестности границы ограничений. Для этого строится градиент к ограничивающей поверхности и соприкасающаяся плоскость, ортогональная градиенту. В качестве возможного направления поиска рассматривается направление, противоположное градиенту. Функции, задающие ограничения, линеаризуются в окрестности допустимой точки.

Если через 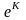обозначить возможное (допустимое) направление поиска из точки , то новая точка определяется соотношением

.

Подставляя в линеаризованные выражения для и 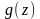вместо значение , приходим к задаче

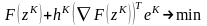, (6.18)

.

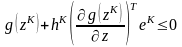Очевидно, точка будет допустимой, если выполняется условие

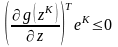, (6.19)

откуда и определяется вектор возможных направлений 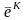, вдоль которых целевая функция имеет наибольшую скорость убывания. Величину шага , как и ранее, можно выбирать путем одномерной минимизации 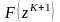по .

Метод работает с ограничениями типа нестрогих неравенств, если в число возможных направлений включаются направления вдоль границы.

Проективный градиентный метод

Метод отличается от метода возможных направлений тем, что при попадании точки в район границы допустимое направление поиска определяется путем проектирования антиградиента 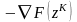на многогранник, являющийся линейной аппроксимацией допустимого множества вблизи точки . Метод позволяет учесть ограничения как типа неравенств, так и типа строгих равенств.

Метод штрафных функций

В этом методе поиск минимального значения целевой функции с учетом ограничений заменяется на поиск минимального значения функции 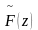- суммы целевой функции и штрафной функции :

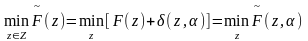, (6.20)

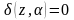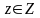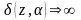где , если , , если .

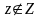При численном решении приходится сталкиваться с овражным характером новой целевой функции. Метод штрафной функции имеет разновидности, связанные с начальным приближением. Если метод может работать только из множества внутренних точек, т.е. когда сразу выполняются ограничения, то он относится к методам внутренней точки. Его задача - препятствовать выходу за ограничения. Методы внешней точки могут начинать работу из любого начального приближения. Если начальное приближение не удовлетворяет ограничениям, то сначала метод «сбрасывает» текущую точку внутрь допустимой области.

40. Пусть задана динамическая система

, , ,

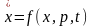где 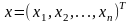- переменные состояния, 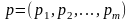- параметры.

Кроме того, на правом конце траектории заданы все или часть переменных состояния:

, , .

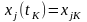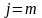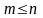Таким образом, выбор параметров должен подчиняться условию:

, .

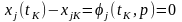Функции 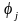называются невязками. Говорят, что поставлена краевая задача порядка .

Параметры могут представлять собой параметры объекта управления или параметры управляющих зависимостей, имеющие физический смысл (например, угол тангажа, угол крена, момент переключения управления и т.д.). При использовании алгоритма принципа максимума (см. раздел 3) параметры могут быть начальными значениями сопряженных переменных и в этом случае они физического смысла не имеют.

С математической точки зрения решение краевой задачи сводится к решению системы нелинейных уравнений, заданной в неявном виде, так как конечные значения переменных состояния могут быть получены только через оператор интегрирования :

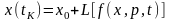. (6.21)

Неявная форма записи нелинейной системы уравнений имеет вид:

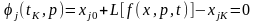. (6.22)

Для начала работы вычислительного алгоритма необходимо задать начальное приближение 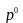. Переход от -го приближения к 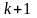-му основан на линейной аппроксимации невязок в окрестности текущей точки :

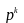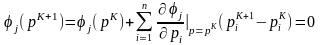. (6.23)

Поскольку обычно невязки зависят от искомых параметров нелинейно, то делается не полный шаг, получающийся из предположения о линейности этих зависимостей, а только его часть, приближающая к решению системы нелинейных уравнений, которая регулируется шагом .

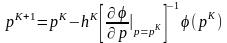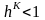, . (6.24)

Матрица частных производных невязок по параметрам имеет размерность и определяется численно, для чего требуется 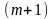интегрирование уравнений движения. Основным требованием сходимости метода является невырожденность этой матрицы.

Величина может подбираться на каждом шаге поиска. Модификация метода заключается в выборе из условия минимизации обобщенной невязки 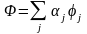, где 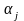- весовые коэффициенты:

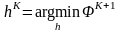. (6.25)

Эта операция требует как минимум трех дополнительных вычислений невязок, если зависимость 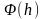аппроксимировать параболой, подобно тому как это было описано в п. 6.5.