
- •1. Задачи математического программирования называются также статическими задачами оптимизации.
- •2. Определение. Переменная величина называется функционалом от функции , если каждой функции из некоторого множества функций соответствует определенное значение .
- •4. Простейшей задачей вариационного исчисления называется задача об экстремуме функционала вида (2.1) с граничными условиями: , .
- •5. . Для того чтобы функционал
- •6. Изопериметрическими задачами, в узком смысле этого слова, называются задачи об отыскании геометрической фигуры максимальной площади при заданном периметре.
- •7. Исследуем на экстремум функционал, зависящий от функций,
- •8. 2.5. Основная формула для вариации функционала
- •12. Введем новые переменные и преобразуем основную формулу для вариации функционала (2.11):
- •15.Выражение для выражение для второй вариации принимает вид
- •18. Введение игольчатой вариации управления [1] позволило получить необходимое условие минимума функционала при ограничениях на управление.
- •19. Следующее дифференциальное уравнение для вектора – функции :
- •6. Окончательно задача оптимального управления приводится к краевой задаче для системы обыкновенных дифференциальных уравнений
- •24. . Задача программирования оптимального управления
- •2. Задача синтеза оптимального управления
- •25. Рассмотрим следующую задачу синтеза оптимального управления линейной динамической системой
- •27. Доказательство принципа максимума было проведено без учета ограничений на вектор состояния. Рассмотрим теперь следующую постановку задача. Дана автономная динамическая система
- •29. Запишем уравнение Беллмана (4.4)
- •30. Рассмотрим решение задачи минимизации, когда функционал содержит только терминальный член: , .
- •31. Рассмотрим следующую задачу синтеза оптимального управления линейной динамической системой
- •32. Рассмотрим задачу оптимального управления дискретной динамической системой
- •33. Рассмотрим линейную дискретную систему
- •34. При решении задачи синтеза оптимального управления нелинейной динамической системой
- •39. Пусть имеется функция , определенная на множестве . Требуется найти
- •40. Пусть задана динамическая система
1. Задачи математического программирования называются также статическими задачами оптимизации.
Формулировка
задачи математического программирования.
Найти вектор
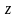 с компонентами
с компонентами
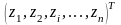 из некоторого допустимого множества
из некоторого допустимого множества
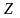 ,
задаваемого в виде ограничений
,
задаваемого в виде ограничений
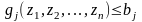
 ,
(1.1)
,
(1.1)
который минимизирует (или максимизирует) целевую функцию
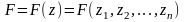 ,
,
т.е.
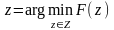 или
или
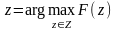 .
(1.2)
.
(1.2)
В
зависимости от вида функций
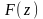 и
и
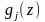 выделены отдельные типы задач, для
которых разработаны специальные методы.
выделены отдельные типы задач, для
которых разработаны специальные методы.
Классические
задачи оптимизации. Отличаются тем,
что среди ограничений, задающих допустимое
множество
,
отсутствуют неравенства, нет условий
неотрицательности или дискретности
переменных, а функции
и
непрерывны и имеют частные производные,
по крайней мере, второго порядка.
Типичными задачами являются задачи на
отыскание минимума (или максимума)
функции
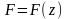 либо в предположении, что на вектор
никаких ограничений не накладывается
(задачи на безусловный экстремум), либо
в предположении, что вектор
связан только равенствами (задачи на
условный экстремум).
либо в предположении, что на вектор
никаких ограничений не накладывается
(задачи на безусловный экстремум), либо
в предположении, что вектор
связан только равенствами (задачи на
условный экстремум).
Эти задачи, как правило, могут быть решены классическими методами, основанными на использовании дифференциального исчисления. Трудности возникают при получении численных результатов, поэтому классические методы являются в большей степени теоретическими.
Задачи линейного программирования. Характеризуются тем, что функции и являются линейными по .
Требуется найти вектор с компонентами , обеспечивающий минимум (или максимум) функции
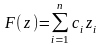 (1.3)
(1.3)
при
условиях
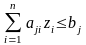 ,
,
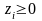
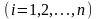 .
.
В основе большинства методов решения задач линейного программирования лежит симплекс-метод [9, 11].
Задачи нелинейного программирования. К ним относятся все задачи с нелинейной целевой функцией или нелинейными ограничениями. Частным случаем являются задачи квадратичного программирования.
Задачи квадратичного программирования. Характеризуются квадратичной зависимостью целевой функции и линейной зависимостью функций . Методы решения задач этого типа в основном базируются на теореме КунаТаккера [4].
Детерминированные задачи. В этих задачах целевая функция является детерминированной (неслучайной) функцией параметров.
Стохастические задачи. Характеризуются тем, что параметры задачи являются случайными величинами, и поэтому целевая функция представляет собой какую-либо статистическую характеристику случайной функции параметров.
Для решения задач нелинейного программирования (как детерминированных, так и стохастических) применяются методы поиска, которые, в свою очередь, могут быть детерминированными и стохастическими.
Детерминированные методы поиска. Имеют жесткий алгоритм поиска (без случайных элементов). К этим методам относятся градиентные методы, метод покоординатного спуска, метод штрафных функций, овражные методы, одномерные методы поиска и другие.
Методы случайного поиска. Характеризуются наличием элемента случайности в алгоритме поиска (например, случайными могут быть величины пробного шага, рабочего шага и другие). К этим методам относятся методы ненаправленного случайного поиска, комбинированные методы поиска, методы случайного поиска с самообучением.
Формулировка вариационной задачи. Дана модель динамической системы
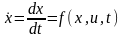 ,
(1.4)
,
(1.4)
где
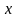 - вектор состояния,
- вектор состояния,
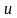 -
вектор управления, на которые накладываются
ограничения
-
вектор управления, на которые накладываются
ограничения
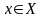 ,
,
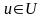 (
(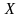 и
и
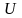 - соответственно допустимые множества
векторов состояния
и управления
).
Поведение системы рассматривается на
некотором конечном отрезке времени
- соответственно допустимые множества
векторов состояния
и управления
).
Поведение системы рассматривается на
некотором конечном отрезке времени
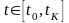 .
Требуется найти такое управление
системой, т.е. вектор
,
которое обращает в минимум или максимум
функционал
.
Требуется найти такое управление
системой, т.е. вектор
,
которое обращает в минимум или максимум
функционал
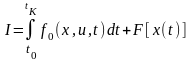 .
.
