23. Колебательный контур. Гармонические и электромагнитные колебания. Дифференциальное уравнение и его решение.

24. Распространение волн в упругой среде. Уравнения плоской и сферической волн.Уравнение плоской волны, распространение в произвольном направлении.

Если в каком-либо месте упругой (твердой, жидкой или газообразной) среды возбудить колебания ее частиц, то вследствие взаимодействия между частицами это колебание начнет распространяться в среде с некоторой скоростью v. Процесс распространения колебаний называется волной. Частицы среды, в которой распространяется волна, не переносятся волной, они лишь совершают колебания около своих положений равновесия. В зависимости от направления колебания частиц по отношению к направлению, в котором распространяется волна, различают продольные и поперечные волны. В продольной волне частицы среды колеблются вдоль направления распространения волны. В поперечной волне частицы среды колеблются в направлениях, перпендикулярных к направлению распространения волны. Механические поперечные волны могут возникнуть лишь в среде, обладающей сопротивлением сдвигу. Поэтому в жидкой и газообразной средах возможно возникновение только продольных волн. В твердой среде возможно возникновение как продольных, так и поперечных волн. В продольных волнах вследствие совпадения направлений колебаний частиц и волны появляются сгущения и разрежения.

Распространение волн в упругой среде.

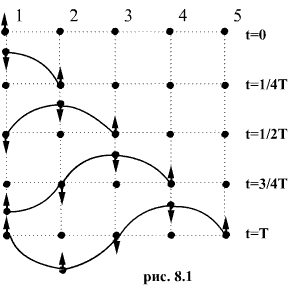
На рис.8.1 показано движение частиц при распространении в среде поперечной волны. Номерами 1,2,3 и т.д. обозначены частицы, отстоящие друг от друга на расстоянии, равном , т.е. на расстоянии, проходимом волной за четверть периода колебаний, совершаемых частицами. В начальный момент времени (t = 0) все точки расположены на прямой и ни одна из них не выходит из положения равновесия. Приведем точку 1 в гармоническое колебание с периодом Т, направленное перпендикулярно линии 1-5. Гак как частицы среды связаны между собой силами упругости, они тоже приходят в колебания, но с некоторым запаздыванием. Через четверть периода точка 1 отклонится от линии равновесия на максимальное смещение. Колебание начали все точки, лежащие слева от точки 2. По истечении времени начнет подниматься вверх и точка 2. При , первая точка вернется в положение равновесия, вторая точка достигнет максимального отклонения, и колебания дойдут до точки 3. При точка 1 достигнет максимального отрицательного смещения, точка 2 вернется в положение равновесия и колебания достигнут точки 4. Наконец, за время, равное периоду t = Т, точка 1 вернется в положение равновесия, совершив полностью одно колебание. Колебания распространились до точки 5, все колеблющиеся точки образуют волну. При дальнейших колебаниях точек волновой процесс распространится вправо от точки 5. В рассмотренном случае образования поперечной волны каждая частица движется только вверх и вниз. У наблюдателя же создается впечатление, что «волна бежит», хотя в действительности происходит только передача движения от одной точки среды к другой.

В момент времени равный периоду (t = Т), точки 1 и 5, находящиеся в положении равновесия, имеют одинаковое смещение и одинаковое направление движения (вверх). Поэтому говорят, что точки I и 5 имеют одинаковые фазы. В отличие от этого точки 1 и 3, хотя смещения у них одинаковы, движутся в противоположные стороны, поэтому говорят, что точки 1 и 3 находятся в противоположных фазах. Расстояния между точками 1 и 5 определяет длину волны λ т.е. длиной волны λ называется, расстояние между ближайшими точками волны, колеблющимися в одинаковых фазах. Периодом волны Т называют время одного полного колебания ее точек. Величина, обратная периоду, называется частотой волны. Скорость волны определяется скоростью распространения колебаний от одной точки среды к другой: Так как то,

(8.1)

Скорость распространения волн тем меньше, чем инертнее среда, т.е. чем больше ее плотность. С другой стороны, она имеет большее значение в более упругой среде, чем в менее упругой. Скорость продольных волн определяется по формуле: , а поперечной:

где ρ- плотность среды, E - модуль Юнга, G - модуль сдвига. Так как для большинства твердых тел E>G то скорость продольных волн больше скорости поперечных.

Составим уравнение, которое позволит находить смещение всякой точки волны в любой момент времени. Пусть в точке В рис.8.2 находится источник колебаний. Волны со скоростью v распространяются от источника колебаний вдоль прямой.

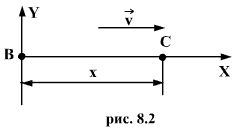
Уравнение колебаний точки В задано в виде:

Все точки вправо от В, например точка С, повторяют колебания точки В с некоторым запозданием. Напишем уравнение колебаний точки С. Если точка В колеблется в течении времени t, то колебания дойдут до точки С по истечении времени , поэтому время колебаний точки С будет меньше t и составит . Тогда уравнение колебаний точки С запишется:

Расстояние от точки В до точки С, равное х, волна проходит со скоростью , откуда . С учетом уравнение волны будет иметь вид:

	(8.2)

где λ - длина волны

Обозначим эта величина называется волновым числом. Тогда получим следующее уравнение

(8.3)

которое называется уравнением плоской одномерной волны и определяет смещение любой точки среды, находящейся на расстоянии х от излучателя в данный момент. Величина

называется фазой волны.

Получим уравнение плоской волны, распространяющейся в направлении, образующем с осями координат х, у, z углы α,β, γ Пусть колебания в плоскости, проходящей через начало координат, имеют вид .

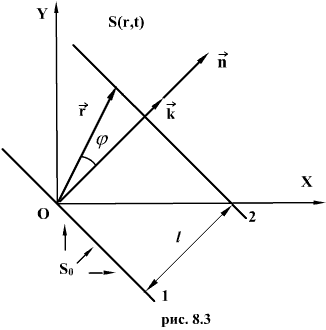
Возьмем волновую поверхность (плоскость), отстоящую от начала координат на расстоянии l. Колебания в этой плоскости будут отставать от колебаний в точке О (рис.8.3) на время тогда уравнение волны

(8.4)

Выразим расстояние l через радиус-вектор точек рассматриваемой поверхности. Для этого введем единичный вектор нормали к волновой поверхности. Скалярное произведение

Подставим значение l в уравнение (8.4) и внесем в скобки

Отношение равно волновому числу k. Вектор равный по модулю волновому числу и имеющий направление вдоль нормали к волновой поверхности называется волновым вектором. Введя вектор , получим

(8.5)

Чтобы перейти от радиуса - вектора точки к ее координатам х, у, z , выразим скалярное произведение через проекции векторов на координатные оси :

Тогда уравнение плоской волны принимает вид:

(8.6)

где