27. Проверка качества многофакторных регрессионных моделей. Оценка качества всего уравнения регрессии.
Качеством модели регрессии называется адекватность построенной модели исходным (наблюдаемым) данным.
Для оценки качества модели регрессии используются специальные показатели.
Качество линейной модели парной регрессии характеризуется с помощью следующих показателей:
парной линейный коэффициент корреляции, который рассчитывается по формуле:
Парный линейный коэффициент корреляции характеризует степень тесноты связи между исследуемыми переменными. Он рассчитывается только для количественных переменных. Чем ближе модуль значения коэффициента корреляции к единице, тем более тесной является связь между исследуемыми переменными.
рассчитываются следующие показатели качества линейной модели множественной регрессии:
множественный коэффициент корреляции между зависимой переменной у и несколькими независимыми переменными хi: Данный коэффициент характеризует степень тесноты связи между зависимой и независимыми переменными. Свойства множественного коэффициента корреляции аналогичны свойствам линейнойго парного коэффициента корреляции.
среднеквадратическая ошибка модели регрессии
где h– это количество параметров, входящих в модель регрессии.Если показатель среднеквадратической ошибки окажется меньше показателя среднеквадратического отклонения наблюдаемых значений зависимой переменной от модельных значений β(у), то модель регрессии можно считать качественной.
3)показатель средней ошибки аппроксимации рассчитывается по формуле:
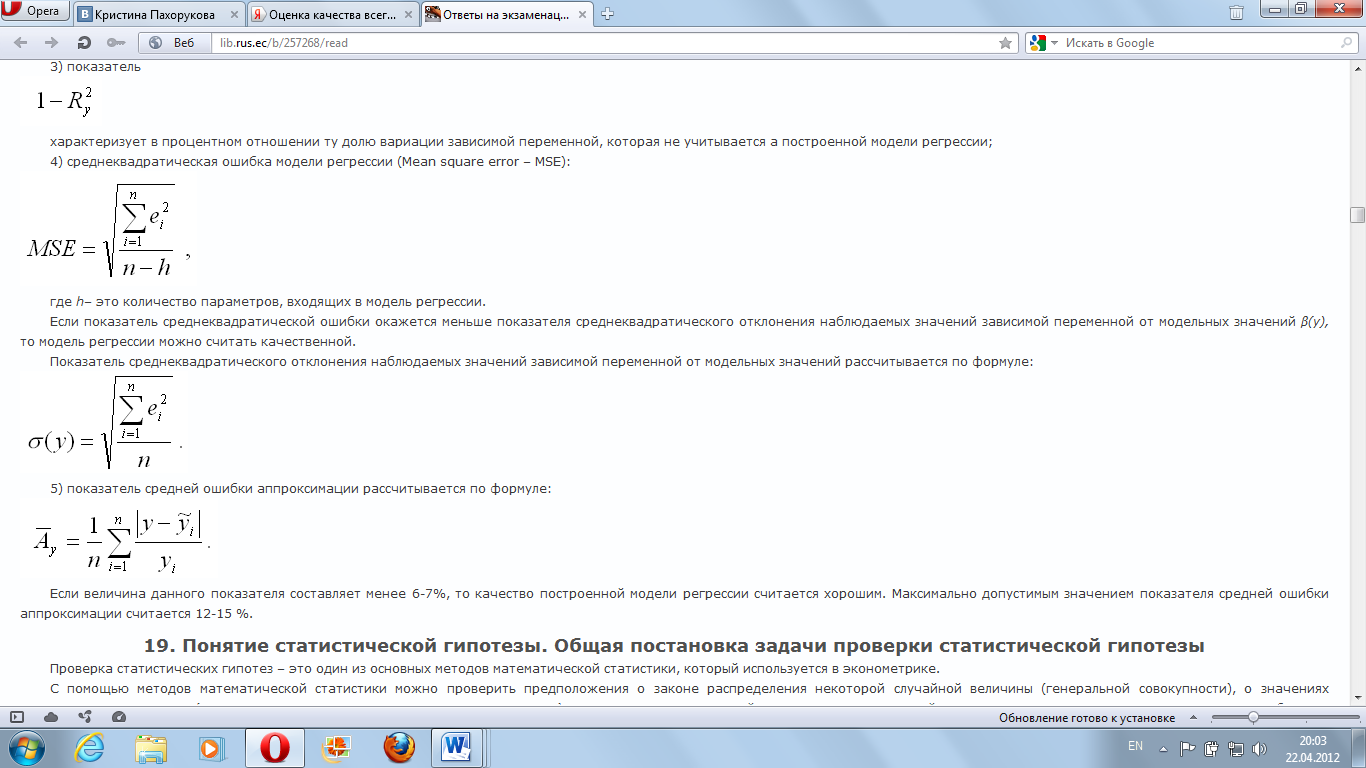Если
величина данного показателя составляет
менее 6-7%, то качество построенной модели
регрессии считается хорошим. Максимально
допустимым значением показателя средней
ошибки аппроксимации считается 12-15 %.
28. Проверка качества многофакторных регрессионных моделей. Коэффициент детерминации . Скорректированный . Проверка гипотез с помощью t-статистик и f-статистик.
После построения модели проверяют ее качество. Одним из показателей качества является коэффициент детерминации. = 1- сумма Ei^2/сумма( yi - yˉ)^2. Одним существенным недостатком коэффициента детерминации является то, что при включении в модель дополнительного регрессора он никогда не уменьшается, а во многих случаях — увеличивается, а это, в свою очередь, приводит к тому, что будет отдано предпочтение варианту уравнения с очень многими регрессорами. С каждым дополнительным регрессором теряется одна степень свободы и этот недостаток не учитывается с помощью, когда он выступает в качестве критерия выбора. С корректированные коэффициенты детерминации призваны учитывать этот факт. Для оценки коэффициента используют статистику Фишера Fрасч. = /m/(1- )/(n-m-1) поэтому Fрасч. Сравнивается с Fтабл. На уровне значимости α=0,05 df1=m df2=(n-m-1). Если Fрасч. больше Fтабл. То модель в целом признается статистически значимой. Для оценки статистической значимости каждого параметра модели находят соответствующие значения t-статистики taj=[aj]/Saj. Находят табличное значение статистики Стьюдента, те параметры модели которые больше tтабл. Признаются статистически значимыми.