Рассмотрим свойства функции f(X).

1. F(-∞)=lim_(x→-∞)F(x)=0. Действительно, по определению, F(-∞)=P{X < -∞}. Событие (X < -∞) является невозможным событием: F(-∞)=P{X < - ∞}=p{V}=0.

2. F(∞)=lim_(x→∞)F(x)=1, так как по определению, F(∞)=P{X < ∞}. Событие Х < ∞ является достоверным событием. Следовательно, F(∞)=P{X < ∞}=p{U}=1.

3. Вероятность того, что случайная величина примет значение из интервала [Α Β] равна приращению функции распределения вероятностей на этом интервале. P{Α ≤X<Β}=F(Β)-F(Α).

4. F(x₂)≥ F(x₁ ), если x_2, > x₁, т.е. функция распределения вероятностей является неубывающей функцией.

5. Функция распределения вероятностей непрерывна слева. FΨ(x_o-0)=limFΨ(x)=FΨ(x_o) при х→ x_o

34. .Что из себя представляет график функции распределения непрерывной случайной величины?

График функции плотности распределения называется кривой распределения, и площадь, ограниченная кривой распределения и осью абсцисс, равна единице. Тогда геометрически значение функции распределения F_(x) в точке х₀ есть площадь, ограниченная кривой распределения и осью абсцисс и лежащая левее точки х₀.

34. Плотность вероятности непрерывной случайной величины и ее свойства.

Плотностью распределения вероятностей непрерывной случайной величины Х называется функция f(x) – первая производная от функции распределения F(x).

Плотность распределения также называют дифференциальной функцией. Для описания дискретной случайной величины плотность распределения неприемлема.

Смысл плотности распределения состоит в том, что она показывает как часто появляется случайная величина Х в некоторой окрестности точки х при повторении опытов.

Свойства плотности распределения

1) Плотность распределения – неотрицательная функция.

2) Несобственный интеграл от плотности распределения в пределах от - ¥ до ¥ равен единице.

34. Геометрический смысл плотности вероятности.

В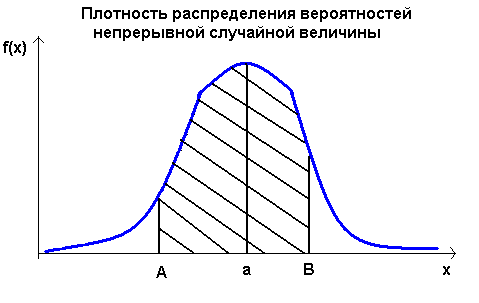 ся кривая плотности распределения вероятностей располагается выше оси 0Х, причем максимум плотности достигается в точке х=а, в которой функция распределения вероятностей имеет наибольшую крутизну. Вероятность попадания случайной величины в интервал [Α ; Β] численно равна площади криволинейной трапеции, построенной на этом интервале как на основании и ограниченной сверху графиком плотности распределения (заштрихованная на рисунке область). Площадь всей криволинейной трапеции, заключенной между осью 0Х и графиком плотности распределения, всегда равна единице. Любая функция, удовлетворяющая перечисленным выше свойствам, может быть плотностью распределения некоторой непрерывной случайной величины.

34. Что из себя представляют числовые характеристики непрерывной случайной величины?

35. Основные законы распределения непрерывной случайной величины:

а) равномерное распределение;

б) нормальное распределение;

34. Перечислите свойства непрерывной случайной величины, распределенной по нормальному закону. Что такое “правило трех сигм”?

35. Сформулируйте закон больших чисел и его следствия.

36. Неравенство Чебышева.

37. В чем заключается особая роль нормального распределения (центральная предельная теорема)?

38. Что изучает математическая статистика?

39. Сформулируйте основные задачи математической статистики.

40. История возникновения и развития математической статистики.

41. Что такое варианты? Дайте понятие ранжированию вариантов.

42. Что называют частотами, частостями (или относительными частотами)?

43. Дайте понятие вариационного рада. Назовите виды вариационных рядов.

44. Перечислите способы графического изображения вариационных рядов. Дайте понятие каждому способу

45. Сформулируйте определение эмпирической функции распределения.

46. Дайте понятие сводным характеристикам вариационных рядов:

а) средним аналитическим величинам (средняя арифметическая, средняя степенная k-го порядка, средняя гармоническая, средняя геометрическая и т.д.);

б) средним структурным (порядковым) величинам (медиана, мода);

в) характеристикам изменчивости (среднее линейное отклонение, дисперсия, среднее квадратическое отклонение).

34. Что называют начальными и центральными моментами?

35. Что понимают под генеральной совокупностью?

36. Что называется выборочной совокупностью или выборкой?

37. Сформулируйте сущность выборочного метола наблюдения.

38. Отметьте преимущества выборочного метода наблюдения по сравнению со сплошным.

39. В чем состоит основной недостаток выборочного метода?

40. Какая выборка называется репрезентативной?

41. Какие различают виды выборок?

66. Перечислите два способа образования выборки

67. В чем включается важнейшая задача выборочного метода?

68. Что называют оценкой параметра?

69. Почему следует судить о качестве оценки?

70. Что означает словосочетание "наилучшая оценка”?

71. Сформулируйте основные свойства оценок.

72. Как определяется эффективность оценки?

73. Какая оценка называется асимптотически эффективной?

74. Перечислите методы оценивания параметров.

75. Что из себя представляет метод моментов?

76. Дайте понятие методу максимального правдоподобия.

77. В чем заключается сущность мегода иаименьших квадратов?

78. Сформулируйте определение интервальной оценки параметров.

79. Что называют доверительным интервалом, доверительной вероятностью? От чего зависит величина доверительного интервала?

80. Что называют предельной ошибкой выборки?

81. Какие подходы могут быть реализованы при построении интервалов?

82. Запишите формулы доверительной вероятности для средней и доли.

83. Дайте понятие средней квадратической (стандартной) ошибки выборки и перечислите ее свойства.

84. Как найти объем выборки?

85. В чем заключается сущность интервальной оценки параметров формального и биноминального распределения?