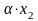24. Перечислите математические операции, выполняемые над случайными величинами. Дайте определение каждой математической операции.

Определение. Случайные величины Х и Y называются равными, если их законы распределения точно совпадают, и для произвольного числа справедливо равенство:

Определение. Случайной величиной называется такая случайная величина, закон распределения которой имеет вид :

:				…
				…

Определение. Случайные величины Х и Y называются независимыми, если для любых i и j события 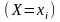и 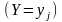– независимы.

Определение. Суммой (разностью, произведением) случайных величин Х и Y называется такая случайная величина ( 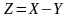, ), которая принимает значение в некотором испытании, если значения и случайных величин Х и в этом испытании таковы, что ( ).

34. Что называется математическим ожиданием случайной дискретной величины? Перечислите свойства математического ожидания.

Математическим ожиданием дискретной случайной величины называется сумма произведений всех возможных значений случайной величины на их вероятности.

Математическое ожидание существует, если ряд, стоящий в правой части равенства, сходится абсолютно.

С точки зрения вероятности можно сказать, что математическое ожидание приближенно равно среднему арифметическому наблюдаемых значений случайной величины.

Свойства математического ожидания

1) Математическое ожидание постоянной величины равно самой постоянной.

2) Постоянный множитель можно выносить за знак математического ожидания.

3) Математическое ожидание произведения двух независимых случайных величин равно произведению их математических ожиданий.

4) Математическое ожидание суммы двух случайных величин равно сумме математических ожиданий слагаемых.

34. Дайте понятие дисперсии дискретной случайной величины. Перечислите свойства дисперсии.

Дисперсией (рассеиванием) дискретной случайной величины называется математическое ожидание квадрата отклонения случайной величины от ее математического ожидания.

Свойства дисперсии:

1)Дисперсия постоянной величины равна нулю.

2) Постоянный множитель можно выносить за знак дисперсии, возводя его в квадрат.

3) Дисперсия суммы двух независимых случайных величин равна сумме дисперсий этих величин.

4) Дисперсия разности двух независимых случайных величин равна сумме дисперсий этих величин.

34. Как найти дисперсию числа появлении события в независимых испытаниях?

Пусть производится п независимых испытаний, в каждом из которых вероятность появления события А постоянна и равна p. Тогда дисперсия числа появлений со­бытия в этих испытаниях вычисляется по формуле:

D(Х)=npq, n – число испытаний, p – вероятность наступления события,   q – вероятность не наступления события

34. Что такое средне квадратическое отклонение?

Средним квадратическим отклонением  случайной величины Х называется квадратный корень из дисперсии.

34. Законы распределения дискретной случайной величины:

а) биноминальное распределение

Случайная величина Х имеет биномиальный закон распределения с параметрам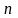и и , если ее закон распределения имеет вид :

Х :		0	1	2	…		,
					…

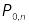
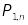
где вероятности 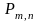вычисляются по формуле Бернулли:

– положительное целое число, ;

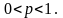б) распределение Пуассона

Говорят, что случайная величина Х имеет распределение Пуассона с параметром , если ее закон распределения имеет вид:

Х :		0	1	2	…	,
					…

где , – положительное число;

в) геометрическое распределение

Пусть   — бесконечная последовательность независимых случайных величин с распределением Бернулли, то есть

Построим случайную величину  - количество «неудач» до первого «успеха». Распределение случайной величины   называется геометрическим с вероятностью «успеха»  , что обозначается следующим образом:  ;

г) гипергеометрическое распределение

Пусть имеется конечная совокупность, состоящая из   элементов. Предположим, что   (defective) из них обладают нужным нам свойством. Оставшиеся   этим свойством не обладают. Случайным образом из общей совокупности выбирается группа из   элементов. Пусть   - случайная величина, равная количеству выбранных элементов, обладающих нужным свойством. Тогда функция вероятности   имеет вид:

,

где   обозначает биномиальный коэффициент. Пишем:  .

Как найти математическое ожидание и дисперсию случайной величины по каждому закону распределения?

34. Сформулируйте определение функции распределения непрерывной случайной величины. Перечислите основные свойства этой функции.

Функцией распределения вероятностей F(x) случайной величины Х в точке х называется вероятность того, что в результате опыта случайная величина примет значение, меньше, чем х, т.е. F(x)=P{X < х}.