Системы управления (курсовой проект) / Задание на курсовое проектирование СУ_2015

рис.14 Структурная схема оптимального регулятора состояния

̂

4

Оптимальный регулятор состояния, являясь наиболее совершенным типом регулятора, требует измерения всех компонентов вектора состояния объекта. Для получения их оценок (x) используется динамическая модель объекта (цифровая или аналоговая), подключенная параллельно исходному ОУ. Для обеспечения равенства движений в реальном объекте и модели используется наблюдатель, который, сравнивая движения векторов Y и Y М , обеспечивает их равенство (E H >0 ). Параметры регулятора состояния рассчитываются методами аналитического конструирования регуляторов

где Q и R — матрицы весов на компоненты вектора состояния и вектора управления.

31

4 Оценка параметров объекта управления по методу наименьших квадратов

Наиболее распространенным методом оценивания параметров, служащим базовым подходом к параметрической идентификации, является метод наименьших квадратов (МНК), который в предположении линейности и дискретности во времени объекта управления приводит к наиболее простым и универсальным решениям. Задача состоит в том, что по имеющимся выборочным данным наблюдений за входным и выходным сигналами с интервалом дискретизации t оцениваются значения параметров, обеспечивающих минимум величины функционала невязки между модельными и фактическими данными.

представляет невязку, определенную как разность между выходом исследуемого объекта и реакцией, вычисленной по модели объекта.

Невязка складывается из неточностей структуры модели, погрешностей измерений и неучтённых взаимодействий среды и объекта. Однако, независимо от происхождения возникающих ошибок, МНК минимизирует сумму квадратичной невязки для дискретных значений.

Оценка по МНК , минимизирующая критерий J, находится из

Важным свойством оценок по МНК является существование только одного локального минимума, совпадающего с глобальным. Поэтому оценкаявляется единственной. Ее значение определяется из условия экстремума функционала:

откуда следует соотношение, определяемое нормальную систему уравнений:

оценки по методу наименьших квадратов получаются решением матричного уравнения:

В некоторых случаях, когда матрица U квадратной матрицей, что имеет место, например, если размер выборки равен числу оцениваемых параметров, или при использовании регрессионного МНК, и имеет обратную матрицу, то

32

В этом случае = , где I – единичная матрица, и оценки по МНК в базисе ортонормальных функций получаются проще = .

Во многих реальных ситуациях процедура параметрической идентификации производится на основе использования конечного числа экспериментальных данных о значениях входного и выходного сигналов. В этом случае для оценивания параметров объекта целесообразно использовать дискретные формы его описания, например АРСС-модель или дискретную передаточную функцию При необходимости, от значений параметров дискретных моделей несложно перейти к параметрам непрерывных описаний.

Будем считать, что процедура структурной идентификации выполнена на предшествующем этапе и порядки числителя и знаменателя передаточной функции модели n и m однозначно заданы. Пусть измерения выполнены на интервале из (n+N) моментов времени и, следовательно, имеются выборки из N измерений для входного и выходного сигналов:

( ) = [ (0), (1), … , ( − 1)] и ( ) = [ ( ), ( + 1), … , ( + )] .(4.9)

На их основе по каждым k экспериментально сделанным измерениям входного и выходного сигналов можно приближенно рассчитать следующее k+1 значение выходной величины. Такое предсказанное значение можно считать его некоторой оценкой, сделанной на основе k предшествующих измерений для последующего k+1 момента времени.

Введем следующие обозначения:

u(k) ,y(k) - экспериментальные данные для входного и выходного воздействий соответственно, полученные в k-тый момент времени;

̂(k)- предсказанное значение выходного сигнала в k-тый момент времени, рассчитанное по совокупности k-1 предшествующих измерений.

Запишем АРСС-модель идентифицируемого объекта при заданных порядках n и m. Будем рассматривать объект без запаздывания, т.к. учет запаздывания не вносит принципиальных особенностей в решение задачи и не меняет размерности расширенного вектора данных и вектора параметров модели, а лишь приводит к появлению задержки в управляющем сигнале на

33

целое число d периодов квантования. Для каждого момента k предсказанное значение выходного сигнала ̂(k) определяется зависимостью:

̂( ) = 1 ( − 1) + + ( − ) + 1 ( − 1) + + ( − ). (4.10)

На основе зависимости система предсказаний для временной выборки из N измерений имеет вид:

представляет определенным образом сформированный массив экспериментальных данных наблюдений за входным и выходным сигналами;

= [ 1 … 1 … ] – вектор параметров модели.

Вматричной форме система предсказаний имеет вид:

аппроксимации, состоящую из погрешностей измерений выходного сигнала

34

0 определяется выражение для оценки, минимизирующее функцию ошибки:

Полученные выражения представляют в явной форме оценку параметров модели методом наименьших квадратов на основе обработки результатов измерений по полной выборке, когда сначала собирается весь объем исходных экспериментальных данных, после чего производится ретроспективная процедура идентификации.

Следует отметить, что изложенный подход обладает существенными недостатками. Во-первых, необходимо проведение сложных вычислительных операций (например, выполнение процедуры обращения многомерных матриц), требующих большого объема оперативной памяти ЭВМ. Во-вторых, невозможно оперативно обрабатывать исходные данные по мере их поступления.

Вследствие этого получили широкое применение вычислительные схемы, свободные от указанных недостатков. Сущность рекуррентных процедур состоит в получении оценки вектора параметров ̂( + 1) на каждом + 1 – ом шаге путем корректировки оценки на предыдущем - ом

1–ому наблюдению входного и выходного сигналов; ( ) – вектор коррекции предыдущей оценки на основании текущих данных, вычисляемый следующим образом:

Где – единичная матрица соответствующей размерности.

35

Вспомогательный вектор ( ), содержащий текущие значения входного сигнала, должен быть рассчитан заранее для подготовки к каждому

Размерность ( ) не зависит от размера выборки и номера наблюдения, и равна [ × ] или [( × ) + ( × ] при использовании определенной модели.

При использовании АРСС - модели вектор или матрица исходных данных U заменяется на матрицу входно-выходных данных, и

вспомогательного вектора (0). Начальные значения могут быть рассчитаны для некоторого l номера наблюдений на основе стандартной процедуры МНК:

где , - выборка из l экспериментальных данных входного и выходного сигналов. Можно выбрать (0) произвольно, или использую имеющуюся априорную информацию. Например, можно использовать следующие значения:

где >> 1 – достаточно большое число.

1.На очередном цикле измерений производится регистрация входного и выходного сигналов и формируется новый вектор данных

( )предыдущей оценки с учетом вновь поступившых данных.

3.Определяется вектор новых оценок параметров ̂( + 1).

4.Производится подготовка к следующему циклу, вычисляется вектор

( + 1).

Этапы 1-4 повторяются на каждом такте процедуры идентификации.

36

Рассмотрим применение полученных алгоритмов реализации МНК для решения задач идентификации.

4.1 Идентификация динамического объекта явным МНК Рассмотрим применение явной формы МНК для параметрической

идентификации той же АРСС – модели объекта второго порядка, с учетом заданных параметров = 2, = 1.

Использование заданной модели для оценок коэффициентов a1, a2, b основе выборки из N (от 1до N) экспериментальных данных приводит к следующей системе уравнений вида:

1 ( − 1) + 2 ( − 2) + ( − 1) = ( )

Матричная форма записи данной модели имеет стандартный вид линейной модели:

С учетом обозначений матрицы входно-выходных данных:

Параметры дискретной модели a1,a2 и b определяются на основе общего соотношения МНК следующим образом:

37

0 = 25, 1 = 36, 2 = 15.

s1=tf([25],[36 15 1])% непрерывная передаточная функция объекта T_end=60;% интервал измерений

dt=0.2;% шаг дискретизации t=0:dt:T_end;% массив дискретного времени

N=length(t);% размер выборки

u=ones(N,1);% моделирование единичного входного воздействия y=lsim(s1,u,t);% моделирование выходного воздействия

n=2;% порядок объекта

R=[y(n:N-1) y(n-1:N-2) u(n:N-1)]; % формирование расширенной матрицы данных

Y=y(n+1:N); % формирование вектора выходных данных betta=inv(R'*R)*R'*Y

% расчет параметров непрерывной модели

T1=dt^2/(1-betta(1)-betta(2))

T2=(betta(2)*T1+T1+dt^2)/dt

K=betta(3)*T1/dt^

Рассчитанные оценки параметров дискретной модели:

a1=1.919; a2=-0.920; b=0.0266;

Рассчитанные оценки параметров непрерывной модели:

T1=37.5243; T2=15.2014; K=25;

Оценки параметров рассчитаны по формулам:

Из полученных результатов видна удовлетворительная точность оценивания параметров. При этом расчетная практика показывает, что метод чувствителен к помехам, их целесообразно отфильтровывать. Для

38

проведения эксперимента необходимо ввести некоторые преобразования в исследуемый объект управления (рис. 15).

Рис.15 Исследуемый объект управления

На представленном рис. 1 регулятор вносит коррективы в динамические характеристики исследуемого объекта управления, поэтому

необходимо исключить влияние регулятора на динамические свойства объекта управления при снятии разгонной характеристики по уровню.

На рис. 2 представлен способ исключения данного влияния.

Рис.16 Исключение влияния регулятора на характеристики ОУ

Коэффициент пропорциональности ПИД регулятора принимает значение равное единице, а дифференциальная и интегральная составляющие принимают значения таким образом, чтобы разорвать цепи передачи сигнала от сравнительного элемента регулятора (между уставкой и измеряемой величиной) до сумматора пропорциональной, интегральной и дифференциальной составляющей. При таких условиях регулятор не вносит никаких «динамических помех» в динамические характеристики объекта

39

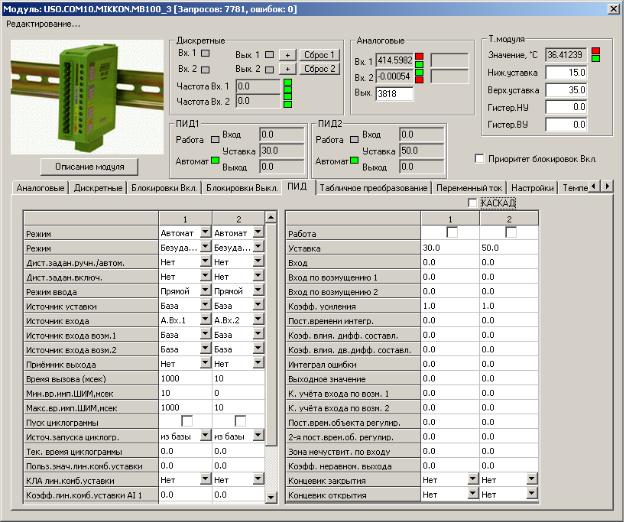
управления. На рис. 3 представлены настройки регулятора на реальном объекте в интерфейсе настройки регулятора модуля УСО MB-100.

Рис.17 Настройки регулятора модуля MB-100 для проведения идентификации динамического ОУ.

В данной вкладке интерфейсе регулятора в правой ее части расположены настроечные коэффициенты регулятора. Для достижения эффекта «динамической прозрачности регулятора» необходимо коэффициент усиления приравнять единице, a1 и a2 постоянные времени объекта регулирования сделать равными нулю. Проведя соответствующие настройки, получим структурную схему для проведения эксперимента по определению разгонной характеристики объекта управления изображенную на рис. 4.

40