Системы управления (курсовой проект) / Задание на курсовое проектирование СУ_2015

где: - постоянная интегрирования, определяющаяся начальными условиями и возмущением; - корни характеристического уравнения являются комплексными:

Как видно соотношение (4) представляет собой синусоиду (частота i) с изменяющейся экспоненциально амплитудой. Если i <0, то составляющая затухает. Если хотя бы одна составляющая из всех n, где n - порядок дифференциальной системы уравнений, будет иметь i >0, система неустойчива. В частном случае, при i =0 , i= i+1=ai переходный процесс носит апериодический характер. В соответствии с этим, для линейных систем будем различать апериодическую и колебательную устойчивость.

Таким образом, суть принятого критерия качества заключается в следующем, чем левее расположен самый правый из комплексных корней (т.е. m отрицательное и максимальное по модулю), тем выше скорость затухания суммарного переходного процесса.

Вернемся к определениям односвязаности и многосвязности системы.

На рис. 5 представлены две одноконтурные структурные схемы регулирования двух разных параметров на некотором, например, тепловом объекте.

Рис. 5 Одноконтурные структурные схемы регулирования двух разных параметров.

11

Предположим для схемы на рис.5.а известны передаточная функция (ПФ) разомкнутой системы Wt (s) от регулирующего воздействия D (например, изменение расхода топлива) к регулируемому параметру T (изменение температуры теплоносителя), а также передаточная функция регулятора в обратной связи t (s). Пусть ПФ и закон регулирования будут простейшими:

Корень характеристического полинома нерегулируемой системы λ (знаменателя ПФ разомкнутой системы Wt (p)) полностью определен величиной постоянной времени Tt и не может быть изменен:

Очевидно, λ имеет отрицательное действительное значение и определяет вид переходного процесса после возмущения как апериодически затухающий по экспоненциальному закону e t . При этом интенсивность затухания зависит от величины λ. Соответственно при замыкании контура регулирования характеристический корень будет определяться из полинома знаменателя замкнутой передаточной функции:

В данном случае, знак и модуль вещественного характеристического корня λ зависят от величины и знака выбранного коэффициента усиления пропорционального регулятора k0. При этом существует однозначная связь: чем больше по модулю отрицательный k0 , тем выше значение функционала качества – степени устойчивости системы. Тем самым представлен простейший пример односвязной системы.

Рассуждения относительно другого автономного (не связанного с первым) контуром регулирования рис.5.б) приводят к аналогичным выводам об односвязности соответствующей ему системы.

Заметим, что при незначительных усложнениях передаточной функции объекта и закона регулирования, при отсутствии взаимного влияния

12

нескольких параметров (или сознательном не учете его) система может сохранять свойство односвязности при управлении или регулировании.

Однако реальные системы управления и их динамические состояния характеризуются вектором взаимозависимых переменных, что часто приводит к противоречивости влияния на них одного и того же управляющего воздействия.

Рассмотрим более реальный пример регулирования рассмотренного теплового объекта, когда учитывается взаимное влияние выходных параметров T (изменение температуры теплоносителя) и P (изменение давления теплоносителя). На рисунке 6 представлен регулируемый объект с параллельным воздействием двух контуров.

Рис.6 Регулируемый объект с параллельным воздействием двух контуров Двухконтурную схему (рис.6) можно представить в виде

одноконтурной (рис.7).

13

Рис.7 – Неявное представление внутренних контуров в системе

Если в системе управления имеется несколько замкнутых контуров с более сложными законами регулирования, например пропорционально –

Очевидно, установить однозначные зависимости между направлением изменения коэффициентов регуляторов, входящих в выражение (8) нелинейно и критерием – степенью устойчивости в полиноме высокого порядка невозможно. Это утверждение является обоснованием и трактовкой свойства многосвязности систем управления.

Под многосвязностью понимается противоречивое взаимное влияние параметров каждого регулятора и регулирующих воздействий различных регуляторов на критерии качества системы (на динамические свойства, степень устойчивости в нашем случае).

Существуют две основные схемы учета многосвязности:

1.Представление структурно объекта в виде системы с вложенными контурами регулирования, как это предложено в рассмотренном примере

14

(рис.6-7). В более общем виде многосвязную систему с множеством вложенных контуров можно представить следующим образом (рис.8):

Рис.8 Многосвязная система с множеством вложенных контуров Передаточная функция замкнутой по всем контурам системы по

любому из параметров (в частности по ) вычисляется согласно соотношению (9):

Вторая схема представление объекта предполагает структуру многомерного объекта, имеющего несколько входных и несколько выходных

переменных, через частные передаточные функции, отражающие

15

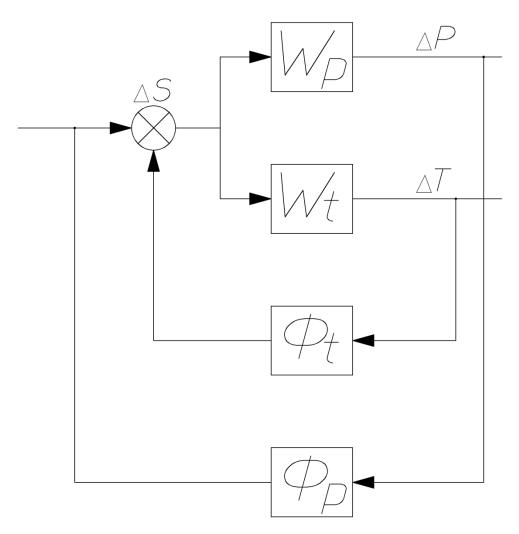
собственное и взаимное влияние параметров и контуров регулирования (рис.8). На этом рисунке, в качестве примера, приведен двухконтурный тепловой объект, где:

T - изменение температуры теплоносителя - выходной параметр первого контура;

-S - изменение расхода топлива - входной параметр первого контура;

-P -изменение давления теплоносителя - выходной параметр второго

контура;

- C - изменение температуры наружного воздуха - входной параметр второго контура;

-1 , 2 - передаточные функции регуляторов первого и второго контуров;

-Wij (p) собственные и взаимные передаточные функции параметров первого

и второго контуров регулирования

16

а)

Рис. 9 – а) структурная схема многосвязной системы с использованием собственных и взаимных передаточных функций. б) структурная схема эквивалентной одноконтурной системы

17

Для перехода к одноконтурной системе необходимо записать выражение для передаточной функции части схемы L11 ,выделенной на рисунке пунктиром:

2 Методы определения свойств объекта.

Динамические свойства объекта полностью описываются системой дифференциальных уравнений. Математический аппарат преобразования Лапласа связывает систему дифференциальных уравнений с другими способами описания динамики объекта - переходной функцией и частотной характеристикой. Причем, переходную функцию и частотную характеристику можно снять экспериментально. Таким образом, возможны два метода определения свойств объекта - аналитический, через систему дифференциальных уравнений и экспериментальный, путем снятия переходных функций и частотных характеристик.

1. Аналитическое описание объекта.

Процесс составления системы дифференциальных уравнений, описывающих динамику объекта, сводится к следующему. Находят уравнение материального или энергетического баланса объекта, выявляя кинетические закономерности, гидродинамические условия и т.д. Далее, от абсолютных значений входных и выходных величин переходят к приращениям в безразмерном виде. Полученные уравнения приводят к каноническому виду.

Составим дифференциальное уравнение системы, образованной двумя баками (рис.1), приняв в качестве входной величины изменение расхода жидкости на притоке G1, а выходной - изменение уровня h2 во втором по ходу жидкости баке. Площади поперечного сечения баков A1 и A

Где

18

1: Расход холодной воды.2: Расход горячей воды.

3: Расход воды от смесителя в втором баке.10: Начальная величина первого расхода.20: Начальная величина второго расхода.1: Изменине первого расхода.

2: Изменине втрового расхода.

К: Постоянная величина. h:Уровень жидкости.

h10:Желаемая величина уровня в смесителе.

Для линеаризации дифференциального уравнения воспользуемся рядом Тейлора:

Воспользовавшись дифференциальным уравнением для бака смешения и применив преобразование Лапласа, получим его передаточную функцию:

Для второго бака аналогично получим:

19

При ∆t→0

dhdt2 = Dh1 − Eh2,

(1.1.8)

Где:

Воспользовавшись дифференциальным уравнением для контрольного (второго) бака, и применяя преобразование Лапласа получим :

Составим дифференциальное уравнение системы управления по температуре (рис 1.):

20