40.Метод ортогонализации Грама-Шмидта, специальные полиномы

Пуст имеется любая система лин независ функций :f₁(x), f₂(x), f₃(x), ….

На первой шаге построим функцию

₁(x) = f₁(x); | ₁>=| f₁>; | >= | >; < | >= =1;

Нормированную функцию построили.

На 2 шаге :

| ₂>=| f₂> - | >< | >; < | > = < | > - < | >< | > =0;

Построили вторую функцию ортогональную первой. Осталось нормировать ее:

| >= | >; < | >=0; =1;

На 3 шаге построим вектор ₃ :

| ₃>=| > - | >< | > - | >< | > ;

< | ₃>=< | > - < | > - 0 = 0;

< | ₃>=< | > - 0 - < | > = 0

Вектор _{3 ортогонален как 1} так и ₂ . Остается его только нормировать :

>= | >.

<f|f> - условие существования

< - условие квадратичной интегрирующей функции

[a,b]		название	условие ортонормир-ти
[-1,1]	1	Полином Лежандра	=δnm
[-1,1]		Чебышева 1-ого рода	=δnm
[-1,1]		Чебышева2 рода	=δnm
[0, ]		Лагерра	=δnm
[ , ]		Эрмита	=…δnm

57. Ф-ия Грина неоднородной КЗ для эрмитова оператора

Вранскиант рассм. решений однородн. ур-ния удовлетворяет решению:

Свойства:

1)Ф-ия Грина непрерывна в основном квадрате, в том числе на диагонали y=x

2)

Производная ф-ии Грина непрерывна в каждом из 2-х основных треугольников

3) - скачок ф-ии на диагонали

4)

5)

58. Сведение задачи Штурма-Лиувилля к интегральному ур-ию

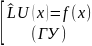(1)

Решение этой задачи может быть записана в след виде:

;

Т.о. задача (1) эквивалентна

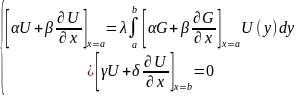
вещественна, симметрична, непрерывна в осн. квадрате

62. Итерированные ядра и их спектры

Ф-ия f(x) есть результат действия некоторого оператора на ф-ию т.е. (

Тогда ур-ие можно записать: - инт-ый оператор

- диф-ый оператор

- симметричная и вещественная ф-ия, которая явл ядром

- ядро оператора

- инт-ые операторы с симметричными ядрами

…

64. Собственные значения итерированного ядра и исходного ядра

Пусть есть СЗ итерированного ядра , а соотв собственная ф-ция есть ψ(х). Пусть 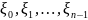- корни из числа . Построим тогда следующие ф-ии:

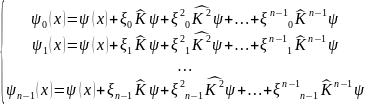
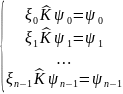- СФ с ядром K

Т.о., по крайней мере один вещественный корень n-ой степени из числа явл СЗ симметричного инт-го ур-ия с ядром

59. Простейшие свойства сиу

(1)

-вещественна, симметрична

– ядро интегрального ур-ия (считается непрерывной ф-ей)

Свойства :

1.(теорема Петровский): симметричное инт-ое ур-ие (1) с непрерывным ядром имеет по крайней мере одно не тривиальное решение

2. если явл решением ур-ия (1), то ф-ия также явл решением этого ур-ия, где С=const

;

3. Вместе с ф-циями решением будет лин комбинация

4:собственные ф-ии, принадлежащие разным собственным значениям ортогональны

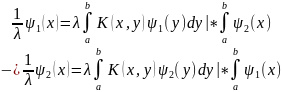
В правых частях обнаружится:

В левых частях:

Если

5. собственные значения симметричных инт-ых ур-ий вещественны

Предположим что СЗ λ –комплексны, тогда

Если ест решение с разными СЗ

6.СФ симметрич интегральных ур-ний могут быть выбраны вещественными

- вещественная ф-ция

7.

Система СФ может быть выбрано ортонормированной

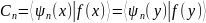
- неравенство Бесселя

8. на всяком отрезке содержится не более чем конечное число СЗ

Предположим что имеется бесконечное количество СЗ, т е

Докажем от обратного:

…

…

Все ф-ции можно нормировать

9. кратность вырождения любого СЗ симметрично и конечно