- •17.Производная разрывной функции и дельта-функции.
- •18.Решение статической задачи с непрерывно распределённой силой.
- •19.Функция Грина статической задачи для струны с (гу)1.
- •21.Различные формы записи общего решения некоторых оду.
- •20.Простейшие статические задачи для струны в упругой среде.
- •22.Статическая задача для струны в упругой среде с точечной силой.
- •23.Статическая задача для струны в упругой среде с непрерывно распределённой силой.
- •24. Метод разделения переменных для волнового уравнения колебаний и уравнения теплопроводности.
- •25. Простейшая задача Штурма-Лиувилля с (гу)1.
- •30.Элементарные решения учп и смешанная задача с простейшими ну.
- •31.Решение зшл с периодическими (гу) в экспоненциальной форме.
- •40.Метод ортогонализации Грама-Шмидта, специальные полиномы
- •58. Сведение задачи Штурма-Лиувилля к интегральному ур-ию
- •62. Итерированные ядра и их спектры
- •64. Собственные значения итерированного ядра и исходного ядра
- •59. Простейшие свойства сиу
- •60. Конечность спектра симметричного интегрального уравнения с вырожденным ядром
- •61. Вырожденность ядра с конечным спектром
- •63. Корни n-ой степени из комплексного числа и их свойства
17.Производная разрывной функции и дельта-функции.
Эта ступенчатая ф-ция наз ф-цией Хевисайда.
Ɵ(х)= ;
Ɵ’(х)=
;
Ɵ’(х)= ;
;
 Ԑ-Ԑ=1;
Ԑ-Ԑ=1;
Ɵ’=δ0(x); dg(x)=g’(x)dx;
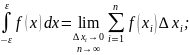 -
интеграл Римана
-
интеграл Римана
 -
интеграл Стильтьеса
-
интеграл Стильтьеса
По определению Стильтьеса можно записать:

dƟ(x)=Ɵ’(x)dx=δ0(x)dx-
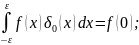
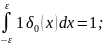
δa(x)=Ɵ’(x-a)= δ0(x-a);
δ0(x-a);
δ0(x)= δ(x); δa(x)= δ(x-a);
 ;
;

Дирак ввел δ функцию и поэтому она часто наз δ ф-цией Дирака. Соболев и Шварц определили, что δ ф-ция явл функционалом
18.Решение статической задачи с непрерывно распределённой силой.
(ОДУ)-TU’’(x)=F(x); (ГУ)1U(0)=0;U(l)=0;
U’’(x)=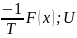 ’(x)=-
’(x)=-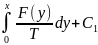 ;
;
 (x)=-
(x)=- ;
;
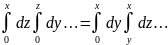 (замена
порядка интегрирования)
(замена
порядка интегрирования)
(x)=-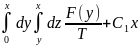 ;
;
(x)=-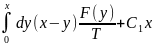 ;
;
(l)=- ;
;
C1=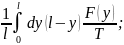
(x)=- - это ответ нашей задачи для непрерывно
распределенной силы
- это ответ нашей задачи для непрерывно
распределенной силы

19.Функция Грина статической задачи для струны с (гу)1.
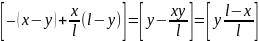 ;
;
U(x)=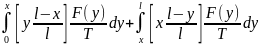 ;
;
Удобно ввести в рассмотрение след функцию:
G(x,y)=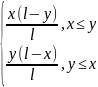 ;
- функция Грина
;
- функция Грина
Тогда
U(x)= ;
;
Функция G(x,y) наз ф-цией Грина для труны. Эта ф-ция задана для х и у, когда они пробегают значения от 0 до l.
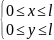 ;
- основной
квадрат
;
- основной
квадрат
Свойства функции: 1)G(x,y) непрерывна в основном квадрате и на диагонали y=x;
2)На всех четырёх сторонах основного квадрата функция Грина обращается в 0: G(0,y)=G(l,y)=G(x,0)=G(x,l)=0—Это св-во ф-ции Грина зад. (ГУ)1
3)Производные ф-ции G(x,y) непрерывны в основном квадрате, за искл.диагонали y=x (на ней производные испытывают скачок)
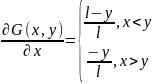
4)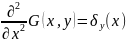 --вторая
производная есть
--вторая
производная есть
 ф-ция
ф-ция
5)Физ.смысл
ф.Грина состоит в том, что G(x,y)= ф-ция Грина есть отклонение струны
под действием силы приложенной к точке.
ф-ция Грина есть отклонение струны
под действием силы приложенной к точке.
21.Различные формы записи общего решения некоторых оду.
-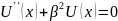 ;
;
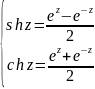 ;
(определение)
;
(определение)
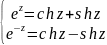 ;
(обращение)
;
(обращение)
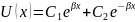 -
общее решение
-
общее решение
U(x)=C1(chβx+shβx)+ C2(chβx-shβx);
C1+C2=A1, C1-C2=B1 (переобозначение);
U(x)=A1chβx+B1shβx; - общее решение
При замене x на l-x имеем:
U(x)=C3eβ(l-x)+ C4e-β (l-x) – ОР
U(x)=A2chβ(l-x)+B2shβ(l-x); -ОР
U(x)=B1shβx+B2shβ(l-x)-ОР …
20.Простейшие статические задачи для струны в упругой среде.
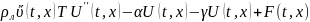 ;
;
U(t,x)=U(x)
-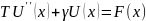 ;
;
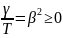
Простейшая
задача:
(ОДУ)-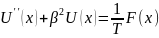 ,
F(x)=0;
,
F(x)=0;
(ГУ)12 ;
;
- ;
Решается методом Эйлера:U(x)=eλx;
U’(x)=λeλx; U’’(x)=λ2 eλx;
-λ2 eλx+β2 eλx=0;
-λ2+ β2=0-характерестическое ур-ие;
β – известная константа, λ - неизвестная
λ1=β и λ2=-β;
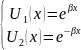 ;
;
- общее решение
U(0)=C11+C21=0; C2=-C1;
U(x)=
C1( -
-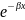 )=2C1shβx;
)=2C1shβx;
U’(x)=2C1βchβx;
T U’(l)= 2C1Tβchβl=F2;
2C1=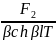 ;
;
U(x)= -ответ
к простейшей задаче;
-ответ
к простейшей задаче;
Если
рассматривать (ГУ)21 ,
то
,
то
U(x)=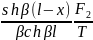
22.Статическая задача для струны в упругой среде с точечной силой.
Рассмотрим случай когда на струну действует точечная сила.
(ОДУ) ;
;
F(x)=Fδa(x);
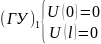 ;
;
 ;
;
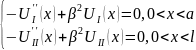 ;
;
 ;
;
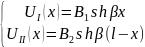 ;
;
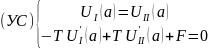 ;
;
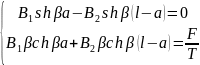 ;
;
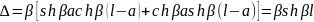 ;
;
 ;
;
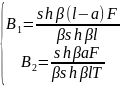 ;
;

Отсутствие упругой среды означает:
 ;
;