31.Решение зшл с периодическими (гу) в экспоненциальной форме.
Расс. тонкий длинный стержень и согнём его в кольцо. L=2l.
(УЧП)
(ГУ) U(t,0)=U(t,L) , kU’(t,0)=kU’(t,L ) - переодические условия
(ОДУ)
X”(x)=
(ГУ)п
X(0)=X(L),
X’(0)=X’(L);
- это и естьЗШЛ с переодич ГУ
1.
;
X”(x)=
;
X(x)=A1
- общее решение.
ГУ
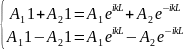
X(x)=ik(A1
).
Запишем систему ГУ в матричном виде:
det=(
=>
;
;
coskL+isinkL=1
coskL=1=>kL=n
;
- CЗ
=>
1
решение:
A1n=
; A2n=0;
2
решение
: A2n=
A1n=0
и
- получили два решения
{
Эти
СФ принадлежат одному СЗ
.
В этом случае говорят, что
двукратно выражено (вырожденное СЗ)
Если λ =0 , то получ решение:
{
},
n = …-2,-1,0,1,2…,
32.Условие ортонормированности СФ ЗШЛ с переодич ГУ.
;
-
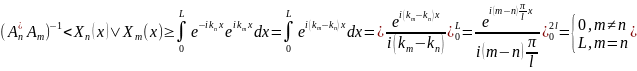
условие ортонормированности
Рассмотрим СмЗ и представим ф-цию U(t,x) в виде:
U(t,x)=
Из
НУ получим:
;
33. коэффициенты ряда фурье и размазанная дельта-функция
Имеется система ф-ций {Xn(x)}. Эта система отртонормированна.
< Xn(x)| Xm(x)>=δnm
=U0(x);
Cn=< Xn(x)| U0(x)>;
Пусть у нас задана нек ф-ция f(x) на нужном отрезке и возникает вопрос о представимости ее в ряд.
f(x)=>Cn=<Xn|f>=> =f(x);
Sn(x)=
=
=<
=
=
;
;
Sn(x)=
;
;
;
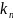=n
;
n
– целое;
;
- размазанная
;
=
34.свойства
размазанной
1.
=
2.
=
– вещ ф-ция
3.
=
- симметричная
4.
=
5.
=
6.
=
- св-во вещественности
7.
=
- четная
8.
=
;
– периодическая
с периодом
9.
dy=1
35.явный вид размазанной
=
α=
[
]
;
=
=
=
+
+..+
=
[1+
+…+
]
=
=
=
=
;
Подставляя
получам след явный вид:
=
.-явный вид размазанной δ- функции
С
помощью этого явного вида можно проверить
все св-ва размазанной
.
36.теорема о поточечной сходимости ряда фурье
Пусть
ф-ция
кусочно-гладкая на отрезке [-
;
],
т.е. кусочно-непрерыв-я
вместе со своей 1-й производ-й, тогда её
ряд Фурье
сходится
в каждой точке отрезка [-
;
]
к самой ф-ции
в точках непрерывности, к выражению
в точках разрыва,
в точках x
= +- l.
37.различные формы рядов Фурье
; =n ; n – целое;
Cn=<
Xn|
f>=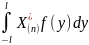
;
f(x)=
=
=
;
Cn=
=
=
;
f(x)=
=
C0+
=
C0+
+
;
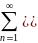f(x)=
+
;
;
.
38.ряды Фурье по собственным функциям ЗШЛ с (ГУ)11 и (ГУ)22
(по синусам или по косинусам)
Пусть на отрезке [0;l]задана ф-ия. продолжим ее нечетным образом:
Из ;
.
=>
а значит в разложении остаются только синусы и получаем:
f(x)=
;
;
=
;
=Bn
;
f(x)=
;
=
.
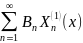Четным образом:
Из ;
.
=>
f(x)=
;
;
=
; f(x)=
;
=
.
39.ряды фурье по ортонормированным системам и сходимость в среднем
U0(x)=
; U0(x)
;
U0(x)-
;
;
- критерий малости
<
(x)|
(x)>=
2
;
{
n(x)};
n=1,2,3…
- любая ортонормированная система
f(x)
;
<ψ (x)|ψ (x)>=δnm;
2 - критерий нормы
2=<
|
>=<
>
=<f|f>+
<
|
>
-
<
|
>
=<f|f>+
-
+
)
-
]
=<
|
>,
=<
|
U0>
- коэф Фурье
2=<f|f>
-
+
- min
=
=<
|
>;
2=
2
-
0;
2
,
;
2
- нер-во
Бесселя
Если
бы
2
это означает что
Если выполняется равенство Бесселя, то система наз полной, и таким образом,она будет полной ортонормированной системой.
<f(x)|g(x)>=
,
где
-весовая
функция