23.Статическая задача для струны в упругой среде с непрерывно распределённой силой.

(ОДУ)-U^’’(x)+β²U(x)=F(x)/T; (ГУ)₁

U(x)=C₁U₁(x)+ C₂U₂(x) – решение однород ОДУ

Нам надо решить неоднород ур-ние. Используем для решения метод вариации:

U(x)=C₁(x)U₁(x)+ C₂(x)U₂(x);

;

;

;

;

- вронскиант

; ;

;

Для определения С1 иС2 нужны еще условия.

U(x)=C₁(x)U₁(x)+ C₂(x)U₂(x);

;

U(x)= - ответ статистич задачи

24. Метод разделения переменных для волнового уравнения колебаний и уравнения теплопроводности.

Расс. ур-ние колебаний струны: (t,x)= ;

U(t,x)=T(t)X(x) => (t,x)= (t)X(x); U”(t,x)=T(t)X”(x)

Подставляем то что у нас получилось в первоначальное ур-ние и получаем: (t)X(x)=

Разделим это ур-ние на T(t) и X(x):

= ; => X”(x)= X(x);

Переменные отделились друг отдруга.

Если нам надо ур-ние теплопроводности: то действуя точно также получили теже ответы: 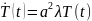- ур-ние с постоянными коэф-тами. Это ур-ние можно решить методом Эйлера.

T(t)=c ; U(t,x0)= c

λ>0 – нет физ смысла, λ<0 – есть физ смысл

(ГУ)₁

25. Простейшая задача Штурма-Лиувилля с (гу)1.

(ОДУ) X(x); (ГУ)1 X(0)=0, X(l)=0 – это и есть ЗШЛ

Необходимо рассм 3 случaя:

1. >0, = .

X”(x)= X(x); X(x)=Ach ᴂx+Bsh ᴂx;

X(0)=A*1+B*0=A=0, X(l)=Bshᴂl=0

b=0 , если λ>0 X(x) только тривиальное решение имеет возможность решения.

2. λ=0.

X”(x)=0; X(x)=A+Bx

Из (ГУ)=>a,b=0 ; X(x) т.е. только тривиальное решение.

3.

X”(x) = ; X(x)= ;

; => , ;

X1(x)= , X2(x)=

ОР строится как лин комбинация с пост коэф: X(x)=c1 +c2

Удобно использовать ф-лу Эйлера: , :

Если подставить формулу Эйлера в общее решение и считать что с1+с2=А; ,то получим общее решения для случая 3:

X(x)=Acoskx=Bsinkx

X(0)=А=0, X(l)= Bsink l= 0

B=0 либо sink l= 0 ; kl= => ; n – целое

X_n(x)=B_n - решение ЗШЛ

Только при таких значениях λ ЗШл имеет решение. Эти значения наз СЗ ЗШЛ с ГУ-1. Соотв им решения наз СФ ЗШЛ.

26. Элементарные решения уравнений в ЧП.

(УЧП) (t,x)= (ГУ) U(t,0)=0, U(t,l)=0

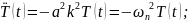
T(t)= -временная зависимость.

Un(t,x)=Tn(t)Xn(x)=[ B

n=0,1,2,3…

Т.о. вспомогательная задача имеет бесконечное множество решений. Такие решения будем наз элементарными.

В случае ур-ния теплопроводности элементарными решениями были бы: Un(t,x)= B_n ;

– основная частота (основной тон). Высшие частоты наз обертоны.

30.Элементарные решения учп и смешанная задача с простейшими ну.

(УЧП) (ГУ)1 U(t,0)=0, U(t,l)=0; (НУ) U(0,x)=U0(x)

Решением явл ф-ция вида:

Un(t,x)=Tn(t)Xn(x)= .

U(t,x)= - лин комбинация так же явл решением

;

(

j ;

Умножим на ф-цию Xm:

=

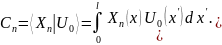
ГУ-1

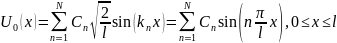
U(t,x)=

ГУ-2 ……

-метод разделения переменных ( закон Фурье).