
- •Изменение энтропии в некоторых равновесных процессах
- •Изменение энтропии в процессе изотермического расширения идеального газа
- •Изменение изменения энтропии в неравновесных процессах
- •Энтропия как функция состояния, определяющая направленность процессов и состояние равновесия в изолированной системе
Изменение энтропии в некоторых равновесных процессах
В
основе этих вычислений лежит уравнение
Клаузиуса
 .
Применим его для вычисления изменения
энтропии при нагревании чистых веществ.
Если оно происходит при постоянном
объеме
.
Применим его для вычисления изменения
энтропии при нагревании чистых веществ.
Если оно происходит при постоянном
объеме


Таким образом, имеем

Аналогично для процесса при постоянном давлении


Обоснованием,
что в уравнениях (1), (3)
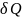 есть элементарные теплоты равновесных
процессов, является то обстоятельство,
что Сv
и
соответственно СР
экспериментально можно определить
только в равновесных, точнее квазиравновесных
процессах. К веществу, теплоемкость
которого предстоит определить, теплота
подводится при минимально возможном
градиенте температур между нагревателем
и веществом. Поэтому на каждом этапе
нагревания от Т1
до
Тк
вещество и теплоисточник находятся по
существу в тепловом равновесии.
есть элементарные теплоты равновесных
процессов, является то обстоятельство,
что Сv
и
соответственно СР
экспериментально можно определить
только в равновесных, точнее квазиравновесных
процессах. К веществу, теплоемкость
которого предстоит определить, теплота
подводится при минимально возможном
градиенте температур между нагревателем
и веществом. Поэтому на каждом этапе
нагревания от Т1
до
Тк
вещество и теплоисточник находятся по
существу в тепловом равновесии.
Теплоемкость определяют по количеству теплоты при очень малых изменениях температуры вещества от Т1 до Т2, отнесенной к интервалу Т2 – Т1 = ∆Т
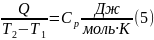
Т2 – Т1 = ∆Т – очень мало
Уравнение
для расчета теплоемкости, например
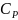 ,
следует из уравнения (3), которое при
очень малом изменении температуры
переходит в соотношение
,
следует из уравнения (3), которое при
очень малом изменении температуры
переходит в соотношение
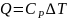
Вычисленную
теплоемкость относят к середине
температурного интервала
 .
.
Определение теплоемкости вплоть до очень низких температур проводят в специальных колориметрах, в которых вещество нагревается электрическим током в тщательно изолированной системе. Колориметры оснащены измерительными устройствами, которые позволяют точно определять количество подводимой электрической энергии (на основе закона Джоуля – Ленца) и температуру образца. Далее на основе уравнения (5) рассчитывают СР.
Г рафическая
зависимость Ср
от температуры при таком способе ее
определения выражается прерывистой
кривой, где соприкасающиеся точки
отвечают значения теплоемкости при
некоторой температуре Т (рис. 1).
рафическая
зависимость Ср
от температуры при таком способе ее
определения выражается прерывистой
кривой, где соприкасающиеся точки
отвечают значения теплоемкости при
некоторой температуре Т (рис. 1).
Ср
а


Т

Рис.1 Зависимость теплоемкости от температуры.
Кривая а в опосредованной форме выражает квазистатический процесс в виде совокупности состояний термического равновесия.
После интегрирования (2), (4) получаем уравнения, которые позволяют определять изменения энтропии при нагревании чистых веществ

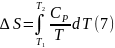
Для вычисления интегралов (6), (7) необходимо располагать зависимостью Сv и СР от температуры. Если есть обоснование считать, что Сv и СР являются постоянными в данном интервале температур, в результате интегрирования имеем

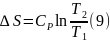
Энтропия – функция состояния и ее изменение зависит только от параметров системы, в данном случае температуры в конце и начале процесса. Изменение энтропии (6 – 9), которое вычислено для равновесного процесса, определяет изменение энтропии не только в этом равновесном процессе, но и в любых других способах нагревания, включая сугубо неравновесные. Необходимое требование для справедливости этого утверждения состоит в том, чтобы температура Т1 в начале и Т2 в конце процесса имели физический смысл параметров состояния. Другими словами вещество в начальном и конечном состоянии должно находится в состоянии внутреннего равновесия.
Уравнения (6 – 9) являются наглядной иллюстрацией соотношения (6) (раздел 4), что хотя изменение свойства не зависит от пути процесса, теоретически его можно вычислить только через физико-математические уравнения равновесного процесса.
Соотношения (2), (4) позволяю не только определять изменение энтропии, но и дают возможность находить зависимость энтропии чистого вещества от температуры. Примеры отыскания функций по заданному дифференциалу рассматриваются в разделе 4. В частности было найдено, что зависимость энтропии одного моля азота от температуры имеет вид

или

где
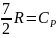 .
.
В отличие от U и Н дл энтропии существуют теоретические основы для вычисления ее абсолютного значения. В основе этих вычислений лежит уравнение (4). Поскольку в итоге определяют стандартную энтропию S0, уравнение (4) используется при стандартном давлении, Р0 = 1атм. При интегрировании (4) в качестве нижнего предела берется абсолютная температура. Верхним пределом может быть любая температура, но в большинстве случаев второй точкой является температура 298,15 К. При заданных начальных условиях имеем


где Т0 = 298,15К.
Для определения S0 необходима температурная зависимость СР в пределах от абсолютного нуля до 289,15К. Другим важным моментом является значение энтропии чистого вещества при абсолютном нуле. Пока можно лишь отметить, что в окрестностях абсолютного нуля чистые вещества находятся в кристаллическом состоянии*.
М. Планк (1911г.) на основе термохимических исследований при низких температурах выдвинул постулат, что энтропия чистого вещества, не имеющего существенных дефектов структуры, при абсолютном нуле равна нулю. Такие кристаллы часто называют идеальными. С точки зрения, что энтропия определяет меру беспорядка системы, идеальные кристаллы при абсолютном нуле находятся в состоянии предельной упорядоченности. Наличие примесей и кристаллических дефектов нарушают идеальную упорядоченность и для таких кристаллов при нулевой температуре S0 ≠ 0.
Зависимость
 определяют ранее описанным экспериментальным
методом. Измерения проводят, начиная с
наиболее низкой температуры. В настоящее
время такой базовой температурой обычно
является температура кипения жидкого
гелия при давлении 1атм (4,2К). Ниже гелиевой
температуры СР
определяют методом
экстраполяции.
Основой для такой экстраполяции является
уравнение, справедливое
определяют ранее описанным экспериментальным
методом. Измерения проводят, начиная с
наиболее низкой температуры. В настоящее
время такой базовой температурой обычно
является температура кипения жидкого
гелия при давлении 1атм (4,2К). Ниже гелиевой
температуры СР
определяют методом
экстраполяции.
Основой для такой экстраполяции является
уравнение, справедливое
_______________________
* За исключением соединений, которые по своей природе являются аморфными, и которые невозможно в принципе перевести в кристаллическое состояние
в области низких температур: теплоемкость пропорциональна Т3: СР = аТ3. Из этого уравнения следует, что при Т → 0, СР→0. Используя данные по теплоемкостях для температур выше температуры кипения гелия, находят значения а, затем проводят экстраполяцию до Т → 0.
Если вещество является твердым вплоть до 298,15К, для S0 имеем
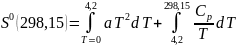
1 2
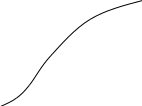
Значение
интегралов 1 и 2 определяют графическим
интегрированием, обычно в координатах
 ,
рис.2.
,
рис.2.

















В



А

Т

СРТ3
4,2 298,15
Рис.2 Метод определения абсолютной энтропии твердого вещества с использованием данных по теплоемкости
В результате графического интегрирования получаем
S0 (298,15) = площадь А + площадь В
С методами определения энтропии жидких веществ и веществ в состоянии идеального газа можно ознакомиться в учебных пособиях по физической химии.
В связи с определением абсолютной энтропии интересно сравнить этот подход с вычислением энтальпии как функции температуры.
В общем случае при Р = const
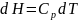
При интегрировании при условии, что Р0 = 1 атм имеем


В отличие от энтропии Н0 (Т = 0) ≠ 0, но ее конкретное значение неизвестно.
Поэтому по уравнению (10) можно вычислить лишь относительное значение энтальпии в результате графического интегрирования выражения () в координатах .

До формулирования принципа Планка энтропию можно было вычислять также как относительную величину. Эта ситуация объясняет появление термина – «абсолютная энтропия».
Найдем зависимость энтропии идеального газа от двух параметров – температуры и давления. Обратимся вновь к равновесному процессу (раздел 4), в котором подводимая теплота используется на повышение температуры газа и на совершение изобарной работы расширения. Первый закон термодинамики в отличие от второго закона термодинамики в одной и той же форме справедлив как для необратимых процессов так и для равновесных.
δQобр = dU + PdV (12)
где PdV – изобарная работа расширения имеет одно и тоже значение, как в равновесных, так и неравновесных процессах.
Разделим обе части уравнения на Т

Используя уравнение состояния идеального газа

или


Для изменения энтропии при условии Сv = const

а б
Таким образом в равновесном процессе (раздел 4) повышение температуры идеального газа с Т1 до Т2 и работа расширения W = Pвнеш (V2 – V1) сопровождается увеличением энтропии (слагаемые «а» и «б» соответственно). Изменение энтропии будет таким же, если процесс будет проходить термодинамически необратимо.
