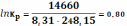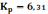3. Основные термодинамические закономерности идеально газовых реакций

С учетом того, что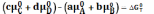 неравенство (4) уравнения (5), (6), (7) приобретают вид

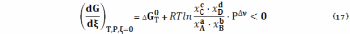
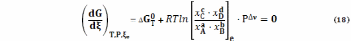
или

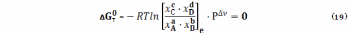
где отношение под знаком логарифма – мольные доли в исходном состоянии (уравнение (17)) и состоянии равновесия.

Уравнения (18), (19) имеют глубокий, но в чем-то неочевидный смысл. Чтобы несколько упростить его выявление, примем, что реакция (1) проходит при Р = 1 атм, что позволяет исключить влияние этого фактора на количество веществ А, В, С, D в состоянии равновесия.

В исходном состоянии состав реакционной системы, определяющий мольные доли в неравенстве (17), был произвольным: 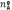, , , . В процессе реакции по мере продвижения к состоянию равновесия уменьшается количество реагентов и увеличивается количество продуктов. Эти изменения связаны стехиометрическим уравнением (1), которое справедливо для любого состава исходной смеси. По этой причине количество веществ n_A, n_B, n_C, n_D и соответствующие мольные доли в состоянии равновесия будут зависеть от состава исходной смеси: каждому индивидуальному составу исходной смеси соответствует индивидуальный состав веществ при равновесии. Но поскольку одна и та же величина при любом составе исходной и соответствующей ему равновесной смеси, величина, равная

также является постоянной при данном значении Т. Это постоянство сохраняется и при умножении отношения равновесных мольных долей на сомножитель , Р – произвольное давление. Из постоянства логарифма величины

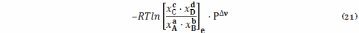
следует, что само отношение под знаком логарифма также постоянная величина. Она обозначается K_p и называется константой химического равновесия идеально газовых реакций.

Таким образом (опуская знак равенства)

С учетом этого, имея в виду уравнения (18), (19)

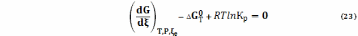
или

= - RTlnK_p (24а)

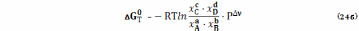
Выражение для константы равновесия (22) можно представить и в более краткой форме

где Р_i – парциальные давления в состоянии равновесия.

Подчеркнем еще раз, что термин «константа равновесия» отражает независимость отношений (22) и (25) от состава равновесной смеси, состав которой в свою очередь определяется составом смеси в исходном состоянии.

Попытаемся это важное положение пояснить на примере реакции

2SО₂ (г) + О₂ (г) = 2SO₃ (г) (26)

Примем, что Т = 950К и Р = 1атм.

Пусть в исходном состоянии находится следующее количество (в молях) веществ

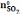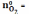Вариант А: = 1; 1; = 1

Вариант В: = 2; 1; = 0

Обозначим через m^* количество молей SO₃, которое образовалось к моменту наступления равновесия. Тогда количество SO₂, которое используется на образование 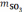можно найти по правилу пропорциональности: в соответствие со стехиометрическим уравнением на образование 2 молей SO₃ необходимо 2 моля SO₂; для m молей SO₃ – y молей SO₂.

2 – 2 y – m

y = m

что для данного варианта очевидно.

Для O₂ аналогичным образом находим**

y = ½ m

В состоянии равновесия (вариант А) имеем

; ;

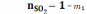Вариант В:

; ;

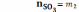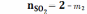Ясно, что из одного моля SO₂ и одного моля O₂ образуется меньше SO₃, чем из двух молей SO₂. Даже при полном превращении SO₂ в SO₃ в первом случае может образоваться лишь 1 моль, во втором – 2 моля.

_______________________

* от лат. «moles» – масса

**При стехиометрическом уравнении

аА + вВ → сС + dD

обозначая количество молей С в состоянии равновесия через m находим:

а – с

yа – m y = m

Аналогично для В и D находим y_В = m; y_D = m

Итак, m₂(В) > m₁(А)

тогда

1 – m₁ ≠ 2 – m₂; 1 – m₁ ≠ 1 – m₂

m₁ ≠ m₂

Общее число молей в состоянии равновесия

А:

B:

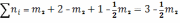
Мольные доли:

А: ; ;

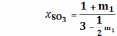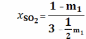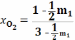
В: ; ;

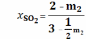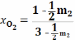
Количество молей и мольные доли в состояниях равновесия, обозначенных А и В различны, но из уравнения (19) следует, что

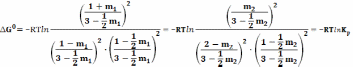
Для реакции (25)(958К) = −14,6 кДж

тогда