10. Составить булеву матрицу для конкретной функциональной модели.

Множество состояний объекта 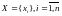; Множество проверок ;. Множество 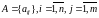результатов проверок

R-множество пар различимых состояний из Х, причем пары 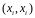исключаются

Рассмотрим простейший случай однократных дефектов (неисправностей) – в любой момент времени неисправен только один функциональный элемент из множества. Введем в рассмотрение множество векторов или набор .

Вектор (набор) 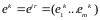определяет подмножество проверок 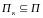, на котором два состояния ОД различимы, при этом соблюдаются следующие условия: если 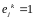, то 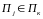и если 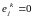, то

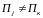
Число элементов в наборе равно числу проверок m.

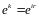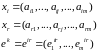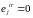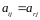
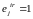Формирование Возьмем 2 состояния объекта , где (из таблицы дефектов): Каждое состояние определяется по следующему правилу: , если , если

Вектор (набор) 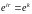определяет подмножество проверок, на котором состояния 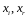различимы. На основе множества векторов строится матрица М

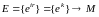
Число столбцов в матрице М равно числу проверок в множестве П, и номер каждого столбца совпадает с номером проверки из П. Т.к. Все пары состояний из R различимы, то матрица М не содержит строк, состоящих только из нулей. Построенную т.о. матрицу называют булевой матрицей.

Пример

Рассмотрим диагностируемый объект, состоящий из 5 функциональных элементов В1,В2,В3,В4,В5, соединенных по схеме (рис. 3); y1,y2,y3,y4,y5 – выходы функциональных элементов (направление внешних воздействий V1 и V2 указаны стрелками). Предположим, что неисправная работа объекта диагностики вызывается наличием только одной неисправности, которая локализуется внутри функционального элемента.

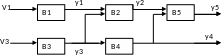
Тогда множество возможных состояний диагностируемого объекта будет состоять из пяти элементов:

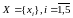
01111 – Х1(в1) – неисправный элемент в1; 10111 – х2(в2) – неисправен в2;и т.Д.

Множество возможных проверок определяется 5-ю элементами

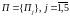П1(y1) – проверка состояния функционального элемента В1 по его выходу y1; и т.д

Тогда табл. состояний диагностируемого объекта запишется в виде:

	П1	П2	П3	П4	П5
х1(В1)	0	0	1	1	0
х2(В2)	1	0	1	1	0
х3(В3)	1	0	0	0	0
х4(В4)	1	1	1	0	0
х5(В5)	1	1	1	1	0

5 Столбец можно исключить

На основании таблицы неисправностей составляют булеву матрицу. Берем попарно неразличимые состояния

	П1	П2	П3	П4
(x1,x2)	1	0	0	0
(x1,x3)	1	0	1	1
(x1,x4)	1	1	0	1
(x1,x5)	1	1	0	0
(x2,x3)	0	0	1	1
(x2,x4)	0	1	0	1
(x2,x5)	0	1	0	0
(x3,x4)	0	1	1	0
(x3,x5)	0	1	1	1
(x4,x5)	0	0	0	1

По данной таблице составляют логическое выражение:

-- 3 проверки

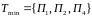
Проверки (по табл. (*)):

1. П1 =0, П2=0, П4=1 – неисправен В1

2. П1=1, П2=0, П4=1 – неисправен В2

3. П1=1, П2=1, П4=0 – неисправен В4

11. Условия Гаусса-Маркова: проверка центрированности остаточного ряда, проверка независимости (некоррелированности) элементов остаточного ряда.

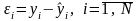(13а) – случайные отклонения, остаточная последовательность, остатки (остаточный ряд).

Оценка адекватности по методу Гаусса – Маркова сводится к анализу остатков.

Условия Гаусса – Маркова:

• остатки имеют случайный характер;

• нулевое математическое ожидание остатков;

• отсутствие корреляции остатков;

• остатки подчиняются нормальному закону распределения.

При выполнении этих условий остатки представляют собой нормальный дискретный белый шум, следовательно, модель соответствует наблюдению.

При выполнении этих условий оценки параметров оказываются несмещенными, эффективными и состоятельными.

• Оценка называется несмещенной, если ;

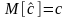• Оценка называется эффективной, если она определена с наименьшей дисперсией (наибольшей точностью);

• Оценка называется состоятельной, если увеличение числа измерений приводит к увеличению точности оценки.

Оценки МНК обладают указанными свойствами.