6. Диагностирование линейных оу методом комплементарного сигнала. Постановка задачи, аналитический расчет кс.

Синтез КС заключается в оценке амплитуд импульсов. Чтобы можно было сигнал использовать для диагностики амплитуда должна быть выбрана таким образом. Чтобы с момента амплитуда . Cостояние объекта, начиная с этого момента, обращается в нулевой вектор.

Решение: Рассмотрим реакцию объекта на единичный скачок при нулевых начальных условиях: , где – n-мерный вектор начального состояния. Для нахождения реакции используется интеграл свертки

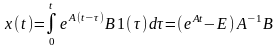(3) Определим состояние объекта в конце первого импульса . В этом случае управляющее воздействие представляет собой единичный импульс . Реакция объекта . Полагая значение первого импульса , матричную экспоненту обозначают и тогда выход: – последовательность состояний объекта. Определим состояния объекта при действии ступенчатого воздействия при ненулевых начальных условиях. Реакция будет включать два составляющих: свободное движение и вынужденное

Перейдя к дискретному времени по следующему правилу:

Тогда 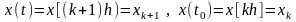. Каждое последующее состояние определяется на основе предыдущего. Связь текущего и предыдущего состояния можно записать в виде рекуррентной формулы (5): (5) Если выбираем для , то в соответствии с формулой (5) получаем:

Выбираем такие , чтобы . В соответствии с теорией Кэли-Гамильтона в качестве коэффициентов надо взять коэффициенты характеристического полинома матрицы .

Собственные числа этой матрицы связанны с собственными числами матрицы А простыми соотношениями . Отсюда в соответствии с теорией Виета, имеем: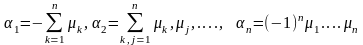 (6)

Алгоритм (аналитический расчет КС)

Данные: матрица А и длительность .

1. По математическому описанию системы рассчитываем ее полюсы

2. По формулам вычисляем собственные числа матрицы .

3. По формулам Виета вычисляем коэффициент , определяющий амплитуды импульсов, составляющих КС.

Комплементарный сигнал содержит n+1 импульс.

7 Аппаратная реализация процесса идентификации.

Объект статический с n – входами и одним выходом. (8) – модель объекта или оценка выхода объекта. (8)

Точность оценивания определяется квадратом отклонения в каждый момент времени: (9) – вектор, т.к. содержит измерения только для одного момента времени:

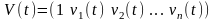
– вектор оценки коэффициентов регрессии. Целью является корректировка и определение оценок в каждый момент времени т.о., чтобы критерий идентификации (9) достигал бы минимума, т.е. в каждый момент времени осуществляется оценивание коэффициентов регрессии (10).

Нахождение оценок коэффициентов регрессии представляется как результат коррекции оценок, полученных ранее (10а). (10) (10a) Используем численный метод оптимизации – градиентный. Текущая оценка определяется на основании предыдущей оценки и некоторой поправки. Поправка – произведение некоторой величины на градиент критерия качества (идентификации). Градиент – вектор, состоящий из частных производных по всем : (11) Градиент – векторное произведение по от критерия идентификации: (12)

С учетом этого производная вектора оценок: (13)

(10а) – рекурсивное выражение переносим влево и делим на интервал между отчетами и устремляем к нулю.