Билет №1

1. Регрессионные модели идентификации: понятия о регрессии, парная и множественная регрессия, ошибка идентификации.

Объект считается статическим, если находится в установившемся (стационарном) состоянии. Модель статического объекта связывается установившимися значениями входных и выходных сигналов.

Регрессионные модели идентификации

, .

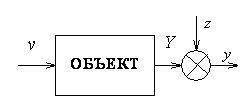
Рассматривается объект с n – наблюдаемыми входами и одним выходом. Кроме того, на выход объекта оказывают влияние ненаблюдаемые входы z. Нельзя говорить о функциональной зависимости между выходом и наблюдаемыми входами, а можно говорить о стохастичности или вероятностной связи.

Упростим задачу, рассматривая объект одним входом и одним выходом . Будем задавать случайный вход и фиксировать выход.

Получаем множество точек с координатами 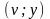– корреляционное поле. Для одного и того же значения входа – множество выходов (выход подвержен влиянию ненаблюдаемых входов). Действие ненаблюдаемых входов z можно интерпретировать как влияние помехи.

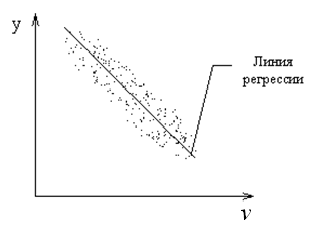
Для того, чтобы установить связь между выходом и входом рассмотрим рисунок

Множество выходов можно заменить средним значением

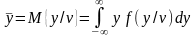(1) где - условная плотность вероятности выхода при данном значении .

Зависимость называется регрессионной:

Соединяя средние точки кривой, получим регрессию . Регрессионная зависимость представляет собой статическую характеристику ОУ.

Если ОУ имеет один вход и один выход, то его характеристикой является простая или парная регрессия: . Если математическое ожидание выхода связно n – входами, то регрессия множественная: 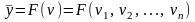В литературе вектор входов называют точкой в факторном пространстве, а 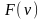– поверхность отклика в факторном пространстве.

К ак простая регрессия, так и множественная, являются моделями статического объекта (с одним и n – входами).

Значение выхода: (2) где – фактическое значение результативного признака (выхода ОУ); – теоретическое значение выхода ОУ, найденное из уравнения регрессии; – случайная величина, обусловленная действием ненаблюдаемых факторов ОУ.

Графически (2) представлено в виде схемы на рис выше.

Мера близости модели и объекта определяется некоторым функционалом ошибки: который зависит от структуры модели вектора параметров.

Оценка модели выполняется на основе минимизации или снижения до определенного уровня значения . Одним из критерия идентификации является критерий качества (4):

(4) Согласно которому оператор можно принять за модель объекта, если максимальное значение модуля ошибки идентификации на интервале наблюдений стремится к минимальной величине. Критерий (4) используется, если входы и выход объекта являются детерминированными функциями(неслучайными). Но, как правило, входные воздействия являются случайными сигналами, поэтому используется критерий (5):   (5)

Выбирается та модель, которая приводит математическое ожидание в минимум. Для практики используется квадратичный критерий качества, значения которых всегда неотрицательны. Для детерминированных сигналов – критерий (6), для аналоговых – критерий (4).

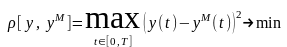, (6)

Для случайных сигналов – критерий (7):

. (7)

. (8)

Критерий (8) используется, если выходы объекта и модели являются непрерывными функциями (функциями с непрерывным временем), если измерение осуществляется дискретно, то используется критерий 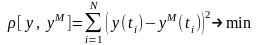(9):

(9)

В случаях 4-9 минимизация осуществляется по оператору . Изменяем структуру и параметры операторов и выбирается с минимальной ошибкой.

2Диагностирование линейных ОУ методом комплементарного сигнала. Процедуры диагностирования, оценка работоспособности ОУ, локализация дефектов по годографу неисправностей.

Объект диагностики представляет собой линейную непрерывную систему, которая заданна описанием в пространстве состояний вида (1). Объект имеет один вход и один выход. 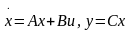(1) Управляющий сигнал представляет собой последовательность разнополярных импульсов длительностью :

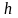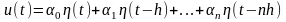(2) где – импульсы. – амплитуды импульсов.

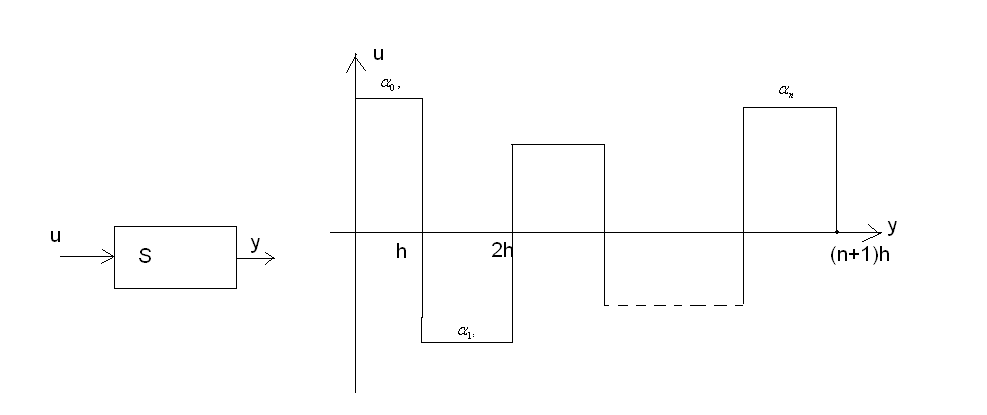Управляющий сигнал имеет вид: - комплементарного сигнала

Требуется составить алгоритмы оценки работоспособности объекта и поиска неисправностей.

Процедура диагностики содержит два этапа:

1. синтез комплементарного сигнала (КС);

2. обнаружение и локализация дефектов.

Аналитический расчет КС

Синтез КС заключается в оценке амплитуд импульсов. Чтобы можно было сигнал использовать для диагностики амплитуда должна быть выбрана таким образом. Чтобы с момента амплитуда 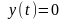. Cостояние объекта, начиная с этого момента, обращается в нулевой вектор.

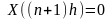
Расчет КС по измеренным значениям выходного сигнала

На вход объекта подается единичный импульс длительностью , – реакция объекта на прямоугольный импульс. 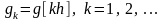– значения реакции в дискретные моменты времени.

(7) Оценки должны быть такими, чтобы с момента времени реакция объекта .

Процедуры диагностирования

Оценка работоспособности ОУ

-Проверка на равенство нулю реакции системы на номинальный КС при ;

-Сравнение экспериментально полученных коэффициентов КС с номинальными коэффициентами.

Локализация дефектов по годографу неисправностей (ГН)

Локализация неисправностей осуществляется путем сравнения фактических значений диагностических признаков с эталонными

КС исправного объекта КС неисправного объекта

– вектор параметров объекта. Характеризующий его работоспособность.

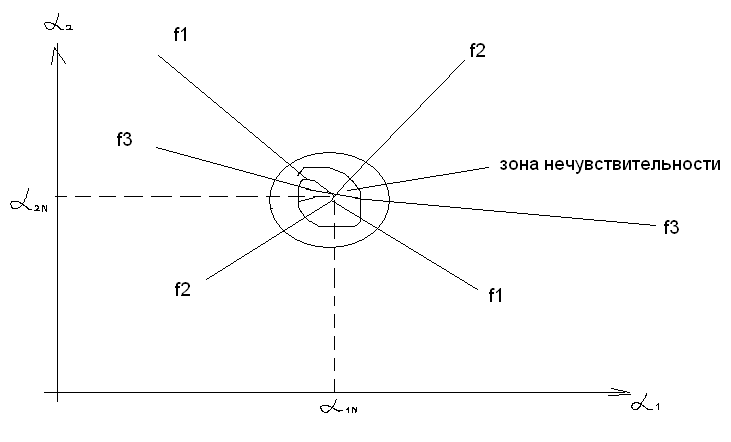
Рассматривается ситуация однократных дефектов. Под действием вариаций параметров изменяет и и на плоскости ( ) точка выписывает некую кривую, которая называется годографом неисправностей. Число годографов равно числу параметров .

Анализ дефектов производится если объект неисправен.

Экспериментально определяется вектор коэффициентов и точка в координатах 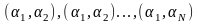. Каждая должна попасть на годограф. Попадание точки например на годограф , который получается в результате вариации параметра , то параметр является недопустимым, то есть дефектным. Если нашли точки , которая является точкой пересечения всех годографов, то этот говорит о работоспособности объекта.

Из формулы (6) следует, что коэффициенты КС определяются только собственными числами матрицы динамики А. Эти собственные числа – полюсы ОУ. То есть корни характеристического многочлена ПФ. Изменение параметров, определяющих работоспособность системы, приводит к изменению коэффициентов . Но некоторые параметры объекта могут влиять и на коэффициенты числителя. Но коэффициенты числителя не используются ни в оценке работоспособности, ни в нахождении дефектов объекта. Поэтому, дефекты, приводящие к изменению коэффициентов числителя ПФ, не могут быть обнаружены этим методом.

3 Численные методы оптимизации, метод Ньютона, особенности метода.