
- •Дробные факторные планы (дробный факторный эксперимент)
- •Ортогональный центральный композиционный план второго порядка.
- •Билет 12
- •13. Условие идентифицируемости автономной динамической системы.
- •14 Применение дробных факторных планов для модели типа (1) и порядок смешивания оценок коэффициентов
- •Билет 14
- •28Планы для моделей, содержащих линейные члены и взаимодействия различного порядка
Билет 14
27 Идентификация нелинейных непрерывных ОУ
ОУ
описывается нелинейным ДУ вида (1):

где
 – i- я производная выхода;
– i- я производная выхода;
 – j- я производная входа;
– j- я производная входа;
 – нелинейная
скалярная функция, подлежащая идентификации
по наблюдениям входа и выхода объекта
– нелинейная
скалярная функция, подлежащая идентификации
по наблюдениям входа и выхода объекта
 .
.
Модель Гаммерштейна
Модель с одним входом и одним выходом.
y(t)
z(t)
v(t)

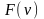



Это
тот случай, когда нелинейный динамический
объект можно представить в виде
последовательного соединения нелинейного
безинерционного звена со статической
характеристикой F
и линейного динамического звена с
весовой функцией
 .
На входе такой модели входное воздействие
.
На входе такой модели входное воздействие
 ,
,
 – оценка выхода объекта (выход модели).
– оценка выхода объекта (выход модели).

Задача идентификации включить оценку двух функций и .
Из схемы модели следует, что выход модели описывается выражением (16).
Покажем, что статические характеристики безинерционного элемента хорошо аппроксимируется степенным рядом (17):
 (17)
(17)
Весовую
функцию линейного динамического звена
разлагаем по системе известных функций
 :
:

Подставляя (17), (18) в (16), получаем:

Введя обозначения получим (19):
 где
где
 .
.
 получим:
получим:

Задача – оценка коэффициентов h.
 – ограниченны
временем регулирования.
– ограниченны
временем регулирования.

Вводим критерий идентификации:

28Планы для моделей, содержащих линейные члены и взаимодействия различного порядка

Коэффициент
 является
мерой парного взаимодействия факторов
(взаимодействия первого порядка),
является
мерой парного взаимодействия факторов
(взаимодействия первого порядка),
коэффициент
 отражает
воздействие тройного взаимодействия
(взаимодействия второго порядка).
отражает
воздействие тройного взаимодействия
(взаимодействия второго порядка).
Применение полных факторных планов для моделей типа (1)
Пример
 ,
,
-
№
v0
v1
v2
v3
v1 v2
у
1
+1
+1
+1
+1
+1
2
+1
–1
+1
+1
–1
3
+1
+1
–1
+1
–1
4
+1
–1
–1
+1
+1
5
+1
+1
+1
–1
+1
6
+1
–1
+1
–1
–1
7
+1
+1
–1
–1
–1
8
+1
–1
–1
–1
+1
а) столбец фиктивного фактора заполняется значениями +1;
б) столбцы входных сигналов заполняется всеми сочетаниями ±1.
в) столбцы взаимодействий входных сигналов заполняются путем перемножения столбцов соответствующих сигналов.
