42. Затухающие колебания. Их характеристики

Затухающие колебания — колебания, энергия которых уменьшается с течением времени. Бесконечно длящийся процесс вида в природе невозможен. Свободные колебания любого осциллятора рано или поздно затухают и прекращаются. Поэтому на практике обычно имеют дело с затухающими колебаниями. Они характеризуются тем, что амплитуда колебаний A является убывающей функцией. Обычно затухание происходит под действием сил сопротивления среды, наиболее часто выражаемых линейной зависимостью от скорости колебаний или её квадрата.

Пускай имеется система, состоящая из пружины (подчиняющейся закону Гука), один конец которой жёстко закреплён, а на другом находится тело массой m. Колебания совершаются в среде, где сила сопротивления пропорциональна скорости с коэффициентом c (см. вязкое трение).

Тогда второй закон Ньютона для рассматриваемой системы запишется так:

где  — сила сопротивления,  — сила упругости

, , то есть

или в дифференциальной форме

где k — коэффициент упругости в законе Гука, c — коэффициент сопротивления, устанавливающий соотношение между скоростью движения грузика и возникающей при этом силой сопротивления.

Для упрощения вводятся следующие обозначения:

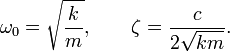
Величину называют собственной частотой системы,  — коэффициентом затухания.

Тогда дифференциальное уравнение принимает вид

Сделав замену , получают характеристическое уравнение

Корни которого вычисляются по следующей формуле

Чем меньше силы трения в системе, тем медленнее затухают колебания, тем лучше колебательная система. Для характеристики качества колебательной системы вводится ряд параметров:

 - время релаксации затухающих колебаний (за   амплитуда уменьшается в e раз).   

   - логарифмический декремент затухания; N - число колебаний, в течение которых амплитуда уменьшается в e раз. Соответственно, exp() - просто декремент затухания.

   - добротность колебательной системы; W(t) - энергия (полная) колебательной системы в момент времени t.

43. Векторы. Действие над векторами. Скалярное и векторное произведение.

Вектор - это направленный отрезок.

Суммой векторов − a(a1;a2) и − b(b1;b2) называется вектор − c a1+b1;a2+b2  , т.е. − a a1;a2 +− b b1;b2 =− c a1+b1;a2+b2  .

Для любых векторов − a(a1;a2)  и − b(b1;b2) справедливы равенства:

• переместительный закон: − a+− b=− b+− a;

• сочетательный закон: − a+(− b+− c)=(− a+− b)+− c;

• из переместительного и сочетательного законов следует, что, складывая любое число векторов, можно как угодно переставлять и группировать слагаемые.

Каковы бы ни были три точки A , B и C , имеет место векторное равенство −− AB+−− BC=−− AC

Правило треугольника: Свойство дает следующий способ построения суммы произвольных векторов − a и − b. Надо от конца вектора − a отложить вектор равный вектору − b. Тогда вектор, начало которого совпадает с началом вектора − a, а конец - с концом вектора − b, будет суммой векторов − a и − b.

Правило параллелограмма: для векторов с общим началом их сумма изображается диагональю параллелограмма, построенного на этих векторах.

Разностью векторов − a(a1;a2) и − b(b1;b2) называют такой вектор − c(c1c2), который в сумме с вектором − b(b1;b2) дает вектор − a(a1;a2). Таким образом: − c(c1c2) + − b(b1;b2) = − a(a1;a2), откуда c₁ = a₁ - b₁ и c₂ = a₂ - b_2.

Правило треугольника. Чтобы найти разность двух векторов, нужно: изобразить их исходящими из одной точки; дополнить чертеж отрезком так. чтобы получился треугольник; придать отрезку направление от вычитаемого к уменьшаемому; этот направленный отрезок и будет вектором разности.

Произведением вектора − a(a1;a2) на число называется вектор − b(b1;b2), такой что b₁ = a₁ и b₂ = a₂. т.е. − a(a1;a2)=− b( a1; a2).

Для любых векторов − a(a1;a2), − b(b1;b2) и чисел ,   справедливы два распределительных закона:

• ( + )− a= − a+ − a 

• (− a+− b)= − a+ − b

Скалярным произведением двух ненулевых векторов называют произведение длин этих векторов на косинус угла между ними: S=− a − b= − a − b cos  , если угол между векторами равен  .

• Если хотя бы один из двух векторов нулевой, то их скалярное произведение равно 0: S=− a − b=0

• Если векторы − a и − b равны, то S=(− a)2 и говорят о скалярном квадрате вектора.В этом случае cos =1, т.е. S= − a 2 . Итак, скалярный квадрат вектора совпадает и квадратом его длины: (− a)2= − a 2 .

• Если векторы − a и − b перпендикулярны, то S=− a − b=0. Векторы − a и − b перпендикулярны в том и только в т ом случае, когда их скалярное произведение равно нулю.

Для любых векторов − a , − b, − c  и числа справедливы равенства:

• ( − a − b)= (− a − b)

• − a(− b+− c)=− a − b+− a − c.

Аналогично рассматриваются вектора и в пространстве.

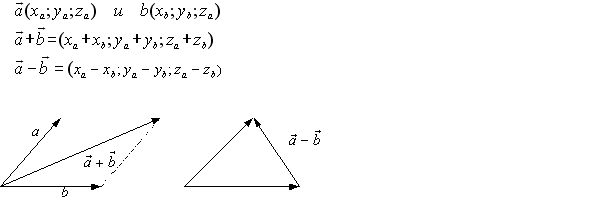
Векторным произведением вектора на вектор в пространстве называется вектор , удовлетворяющий следующим требованиям:

• длина вектора равна произведению длин векторов и на синус угла между ними: ;

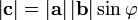• вектор ортогонален каждому из векторов и ;

• вектор направлен так, что тройка векторов 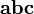является правой;

• в случае пространства 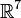требуется ассоциативность тройки векторов .

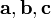Обозначение: