38. Пружинные маятники(горизонтальный и вертикальный)

Пружинный маятник — это колебательная система, состоящая из материальной точки массой т и пружины. Рассмотрим горизонтальный пружинный маятник (рис. 13.12, а). Он представляет собой массивное тело, просверленное посередине и надетое на горизонтальный стержень, вдоль которого оно может скользить без трения (идеальная колебательная система). Стержень закреплен между двумя вертикальными опорами. К телу одним концом прикреплена невесомая пружина. Другой ее конец закреплен на опоре, которая в простейшем случае находится в покое относительно инерциальной системы отсчета, в которой происходят колебания маятника. В начале пружина не деформирована, и тело находится в положении равновесия С. Если, растянув или сжав пружину, вывести тело из положения равновесия, то со стороны деформированной пружины на него начнет действовать сила упругости, всегда направленная к положению равновесия. Пусть мы сжали пружину, переместив тело в положение А, и отпустили Под действием силы упругости оно станет двигаться ускоренно. При этом в положении А на тело действует максимальная сила упругости, так как здесь абсолютное удлинение x_m пружины наибольшее. Следовательно, в этом положении ускорение максимальное. При движении тела к положению равновесия абсолютное удлинение пружины уменьшается, а следовательно, уменьшается ускорение, сообщаемое силой упругости. Но так как ускорение при данном движении сонаправлено со скоростью, то скорость маятника увеличивается и в положении равновесия она будет максимальна. Достигнув положения равновесия С, тело не остановится (хотя в этом положении пружина не деформирована, и сила упругости равна нулю), а обладая скоростью, будет по инерции двигаться дальше, растягивая пружину. Возникающая при этом сила упругости направлена теперь против движения тела и тормозит его. В точке D скорость тела окажется равной нулю, а ускорение максимально, тело на мгновение остановится, после чего под действием силы упругости начнет двигаться в обратную сторону, к положению равновесия. Вновь пройдя его по инерции, тело, сжимая пружину и замедляя движение, дойдет до точки А (так как трение отсутствует), т.е. совершит полное колебание. После этого движение тела будет повторяться в описанной последовательности. Итак, причинами свободных колебаний пружинного маятника являются действие силы упругости, возникающей при деформации пружины, и инертность тела.

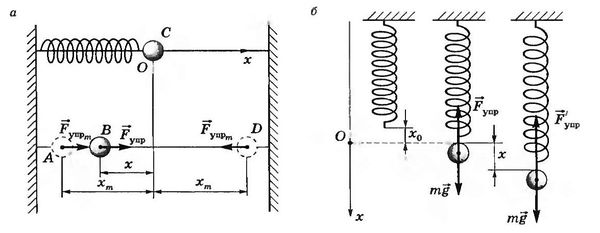
Рис. 13.12

По закону Гука По второму закону Ньютона Следовательно, Отсюда

или — динамическое уравнение движения пружинного маятника.

Видим, что ускорение прямопропорционально смешению и противоположно ему направлено. Сравнивая полученное уравнение с уравнением гармонических колебаний видим, что пружинный маятник совершает гармонические колебания с циклической частотой Так как то

— период колебаний пружинного маятника.

По этой же формуле можно рассчитывать и период колебаний вертикального пружинного маятника (рис. 13.12. б). Действительно, в положении равновесия благодаря действию силы тяжести пружина уже растянута на некоторую величину x₀, определяемую соотношением При смещении маятника из положения равновесия O на х проекция силы упругости и по второму закону Ньютона Подставляя сюда значение получим уравнение движения маятника совпадающее с уравнением движения горизонтального маятника.